| Revision as of 11:03, 23 November 2018 edit196.8.123.44 (talk)No edit summary← Previous edit | Revision as of 15:04, 23 November 2018 edit undoMindmatrix (talk | contribs)Autopatrolled, Administrators187,619 editsm revert - "most" is correct hereNext edit → | ||
| Line 4: | Line 4: | ||
| {{Use dmy dates|date=June 2013}} | {{Use dmy dates|date=June 2013}} | ||
| '''Benford's law''', also called '''Newcomb-Benford's law''', '''law of anomalous numbers''', and '''first-digit law''', is an observation about the ] of leading digits in many real-life sets of numerical ]. The law states that in many naturally occurring collections of numbers, the leading ] is likely to be small.<ref name=BergerHill2011/> For example, in sets that obey the law, the number {{formatnum:1}} appears as the most significant digit about 30% of the time, while {{formatnum:9}} appears as the |
'''Benford's law''', also called '''Newcomb-Benford's law''', '''law of anomalous numbers''', and '''first-digit law''', is an observation about the ] of leading digits in many real-life sets of numerical ]. The law states that in many naturally occurring collections of numbers, the leading ] is likely to be small.<ref name=BergerHill2011/> For example, in sets that obey the law, the number {{formatnum:1}} appears as the most significant digit about 30% of the time, while {{formatnum:9}} appears as the most significant digit less than 5% of the time. If the digits were distributed uniformly, they would each occur about 11.1% of the time.<ref>{{cite web | url=http://mathworld.wolfram.com/BenfordsLaw.html|author = Weisstein, Eric W.| title=Benford's Law | website = MathWorld, A Wolfram web resource |access-date = 7 June 2015}}</ref> Benford's law also makes predictions about the distribution of second digits, third digits, digit combinations, and so on. | ||
| The graph to the right shows Benford's law for ]. There is a generalization of the law to numbers expressed in other bases (for example, ]), and also a generalization from leading 1 digit to leading ''n'' digits. | The graph to the right shows Benford's law for ]. There is a generalization of the law to numbers expressed in other bases (for example, ]), and also a generalization from leading 1 digit to leading ''n'' digits. | ||
Revision as of 15:04, 23 November 2018
Not to be confused with the unrelated adage Benford's law of controversy.
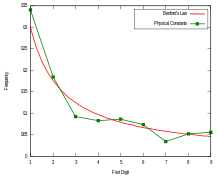
Benford's law, also called Newcomb-Benford's law, law of anomalous numbers, and first-digit law, is an observation about the frequency distribution of leading digits in many real-life sets of numerical data. The law states that in many naturally occurring collections of numbers, the leading significant digit is likely to be small. For example, in sets that obey the law, the number 1 appears as the most significant digit about 30% of the time, while 9 appears as the most significant digit less than 5% of the time. If the digits were distributed uniformly, they would each occur about 11.1% of the time. Benford's law also makes predictions about the distribution of second digits, third digits, digit combinations, and so on.
The graph to the right shows Benford's law for base 10. There is a generalization of the law to numbers expressed in other bases (for example, base 16), and also a generalization from leading 1 digit to leading n digits.
It has been shown that this result applies to a wide variety of data sets, including electricity bills, street addresses, stock prices, house prices, population numbers, death rates, lengths of rivers, physical and mathematical constants. Like other general principles about natural data — for example the fact that many data sets are well approximated by a normal distribution — there are illustrative examples and explanations that cover many of the cases where Benford's law applies, though there are many other cases where Benford's law applies that resist a simple explanation. It tends to be most accurate when values are distributed across multiple orders of magnitude, especially if the process generating the numbers is described by a power law (which are common in nature).
It is named after physicist Frank Benford, who stated it in 1938 in a paper titled "The Law of Anomalous Numbers", although it had been previously stated by Simon Newcomb in 1881.
Definition

A set of numbers is said to satisfy Benford's law if the leading digit d (d ∈ {1, ..., 9}) occurs with probability
The leading digits in such a set thus have the following distribution:
| d | | Relative size of |
|---|---|---|
| 1 | 30.1% | 30.1 |
| 2 | 17.6% | 17.6 |
| 3 | 12.5% | 12.5 |
| 4 | 9.7% | 9.7 |
| 5 | 7.9% | 7.9 |
| 6 | 6.7% | 6.7 |
| 7 | 5.8% | 5.8 |
| 8 | 5.1% | 5.1 |
| 9 | 4.6% | 4.6 |
The quantity is proportional to the space between d and d + 1 on a logarithmic scale. Therefore, this is the distribution expected if the mantissae of the logarithms of the numbers (but not the numbers themselves) are uniformly and randomly distributed.
For example, a number x, constrained to lie between 1 and 10, starts with the digit 1 if 1 ≤ x < 2, and starts with the digit 9 if 9 ≤ x < 10. Therefore, x starts with the digit 1 if log 1 ≤ log x < log 2, or starts with 9 if log 9 ≤ log x < log 10. The interval is much wider than the interval (0.30 and 0.05 respectively); therefore if log x is uniformly and randomly distributed, it is much more likely to fall into the wider interval than the narrower interval, i.e. more likely to start with 1 than with 9; the probabilities are proportional to the interval widths, giving the equation above (as well as the generalization to other bases besides decimal).
Benford's law is sometimes stated in a stronger form, asserting that the fractional part of the logarithm of data is typically close to uniformly distributed between 0 and 1; from this, the main claim about the distribution of first digits can be derived.
Benford's law in other bases

An extension of Benford's law predicts the distribution of first digits in other bases besides decimal; in fact, any base b ≥ 2. The general form is:
For b = 2 (the binary number system), Benford's law is true but trivial: All binary numbers (except for 0) start with the digit 1. (On the other hand, the generalization of Benford's law to second and later digits is not trivial, even for binary numbers.)
Example
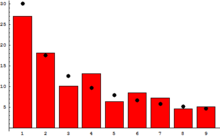
Examining a list of the heights of the 60 tallest structures in the world by category shows that 1 is by far the most common leading digit, irrespective of the unit of measurement (cf. "scale invariance", below):
| Leading digit | meters | feet | In Benford's law | ||
|---|---|---|---|---|---|
| Count | % | Count | % | ||
| 1 | 26 | 43.3% | 18 | 30.0% | 30.1% |
| 2 | 7 | 11.7% | 8 | 13.3% | 17.6% |
| 3 | 9 | 15.0% | 8 | 13.3% | 12.5% |
| 4 | 6 | 10.0% | 6 | 10.0% | 9.7% |
| 5 | 4 | 6.7% | 10 | 16.7% | 7.9% |
| 6 | 1 | 1.7% | 5 | 8.3% | 6.7% |
| 7 | 2 | 3.3% | 2 | 3.3% | 5.8% |
| 8 | 5 | 8.3% | 1 | 1.7% | 5.1% |
| 9 | 0 | 0.0% | 2 | 3.3% | 4.6% |
Another example is the leading digit of 2:
History
The discovery of Benford's law goes back to 1881, when the American astronomer Simon Newcomb noticed that in logarithm tables the earlier pages (that started with 1) were much more worn than the other pages. Newcomb's published result is the first known instance of this observation and includes a distribution on the second digit, as well. Newcomb proposed a law that the probability of a single number N being the first digit of a number was equal to log(N + 1) − log(N).
The phenomenon was again noted in 1938 by the physicist Frank Benford, who tested it on data from 20 different domains and was credited for it. His data set included the surface areas of 335 rivers, the sizes of 3259 US populations, 104 physical constants, 1800 molecular weights, 5000 entries from a mathematical handbook, 308 numbers contained in an issue of Reader's Digest, the street addresses of the first 342 persons listed in American Men of Science and 418 death rates. The total number of observations used in the paper was 20,229. This discovery was later named after Benford (making it an example of Stigler's Law).
In 1995, Ted Hill proved the result about mixed distributions mentioned below.
Explanations
Overview
Benford's law tends to apply most accurately to data that are distributed uniformly across several orders of magnitude. As a rule of thumb, the more orders of magnitude that the data evenly covers, the more accurately Benford's law applies. For instance, one can expect that Benford's law would apply to a list of numbers representing the populations of UK settlements, or representing the values of small insurance claims. But if a "village" is defined as a settlement with population between 300 and 999, or a "small insurance claim" is defined as a claim between $50 and $99, then Benford's law will not apply.
Consider the probability distributions shown below, referenced to a log scale. In each case, the total area in red is the relative probability that the first digit is 1, and the total area in blue is the relative probability that the first digit is 8.

 |
For the left distribution, the size of the areas of red and blue are approximately proportional to the widths of each red and blue bar. Therefore, the numbers drawn from this distribution will approximately follow Benford's law. On the other hand, for the right distribution, the ratio of the areas of red and blue is very different from the ratio of the widths of each red and blue bar. Rather, the relative areas of red and blue are determined more by the height of the bars than the widths. Accordingly, the first digits in this distribution do not satisfy Benford's law at all.
Thus, real-world distributions that span several orders of magnitude rather uniformly (e.g. populations of villages / towns / cities, stock-market prices), are likely to satisfy Benford's law to a very high accuracy. On the other hand, a distribution that is mostly or entirely within one order of magnitude (e.g. heights of human adults, or IQ scores) is unlikely to satisfy Benford's law very accurately, or at all. However, it is not a sharp line: As the distribution gets narrower, the discrepancies from Benford's law typically increase gradually.
In terms of conventional probability density (referenced to a linear scale rather than log scale, i.e. P(x)dx rather than P(log x) d(log x)), the equivalent criterion is that Benford's law will be very accurately satisfied when P(x) is approximately proportional to 1/x over several orders-of-magnitude variation in x.
This discussion is not a full explanation of Benford's law, because we have not explained why we so often come across data-sets that, when plotted as a probability distribution of the logarithm of the variable, are relatively uniform over several orders of magnitude.
Multiplicative fluctuations
Many real-world examples of Benford's law arise from multiplicative fluctuations. For example, if a stock price starts at $100, and then each day it gets multiplied by a randomly chosen factor between 0.99 and 1.01, then over an extended period the probability distribution of its price satisfies Benford's law with higher and higher accuracy.
The reason is that the logarithm of the stock price is undergoing a random walk, so over time its probability distribution will get more and more broad and smooth (see above). (More technically, the central limit theorem says that multiplying more and more random variables will create a log-normal distribution with larger and larger variance, so eventually it covers many orders of magnitude almost uniformly.) To be sure of approximate agreement with Benford's Law, the distribution has to be approximately invariant when scaled up by any factor up to 10; a lognormally distributed data set with wide dispersion would have this approximate property.
Unlike multiplicative fluctuations, additive fluctuations do not lead to Benford's law: They lead instead to normal probability distributions (again by the central limit theorem), which do not satisfy Benford's law. For example, the "number of heartbeats that I experience on a given day" can be written as the sum of many random variables (e.g. the sum of heartbeats per minute over all the minutes of the day), so this quantity is unlikely to follow Benford's law. By contrast, that hypothetical stock price described above can be written as the product of many random variables (i.e. the price change factor for each day), so is likely to follow Benford's law quite well.
Multiple probability distributions
Formann provided an alternative explanation by directing attention to the interrelation between the distribution of the significant digits and the distribution of the observed variable. He showed in a simulation study that long right-tailed distributions of a random variable are compatible with the Newcomb-Benford law, and that for distributions of the ratio of two random variables the fit generally improves. For numbers drawn from certain distributions (IQ scores, human heights) the Law fails to hold because these variates obey a normal distribution which is known not to satisfy Benford's law, since normal distributions can't span several orders of magnitude and the mantissae of their logarithms will not be (even approximately) uniformly distributed. However, if one "mixes" numbers from those distributions, for example by taking numbers from newspaper articles, Benford's law reappears. This can also be proven mathematically: if one repeatedly "randomly" chooses a probability distribution (from an uncorrelated set) and then randomly chooses a number according to that distribution, the resulting list of numbers will obey Benford's Law. A similar probabilistic explanation for the appearance of Benford's Law in everyday-life numbers has been advanced by showing that it arises naturally when one considers mixtures of uniform distributions.
Scale invariance
If there is a list of lengths, the distribution of first digits of numbers in the list may be generally similar regardless of whether all the lengths are expressed in metres, or yards, or feet, or inches, etc.
This is not always the case. For example, the height of adult humans almost always starts with a 1 or 2 when measured in meters, and almost always starts with 4, 5, 6, or 7 when measured in feet.
But consider a list of lengths that is spread evenly over many orders of magnitude. For example, a list of 1000 lengths mentioned in scientific papers will include the measurements of molecules, bacteria, plants, and galaxies. If one writes all those lengths in meters, or writes them all in feet, it is reasonable to expect that the distribution of first digits should be the same on the two lists.
In these situations, where the distribution of first digits of a data set is scale invariant (or independent of the units that the data are expressed in), the distribution of first digits is always given by Benford's Law.
For example, the first (non-zero) digit on this list of lengths should have the same distribution whether the unit of measurement is feet or yards. But there are three feet in a yard, so the probability that the first digit of a length in yards is 1 must be the same as the probability that the first digit of a length in feet is 3, 4, or 5; similarly the probability that the first digit of a length in yards is 2 must be the same as the probability that the first digit of a length in feet is 6, 7, or 8. Applying this to all possible measurement scales gives the logarithmic distribution of Benford's law.
Applications
Accounting fraud detection
In 1972, Hal Varian suggested that the law could be used to detect possible fraud in lists of socio-economic data submitted in support of public planning decisions. Based on the plausible assumption that people who make up figures tend to distribute their digits fairly uniformly, a simple comparison of first-digit frequency distribution from the data with the expected distribution according to Benford's Law ought to show up any anomalous results. Following this idea, Mark Nigrini showed that Benford's Law could be used in forensic accounting and auditing as an indicator of accounting and expenses fraud. In practice, applications of Benford's Law for fraud detection routinely use more than the first digit.
Legal status
In the United States, evidence based on Benford's law has been admitted in criminal cases at the federal, state, and local levels.
Election data
Benford's Law has been invoked as evidence of fraud in the 2009 Iranian elections, and also used to analyze other election results. However, other experts consider Benford's Law essentially useless as a statistical indicator of election fraud in general.
Macroeconomic data
Similarly, the macroeconomic data the Greek government reported to the European Union before entering the eurozone was shown to be probably fraudulent using Benford's law, albeit years after the country joined.
Price digit analysis
Benford's law as a benchmark for the investigation of price digits has been successfully introduced into the context of pricing research. The importance of this benchmark for detecting irregularities in prices was first demonstrated in a Europe-wide study which investigated consumer price digits before and after the euro introduction for price adjustments. The introduction of the euro in 2002, with its various exchange rates, distorted existing nominal price patterns while at the same time retaining real prices. While the first digits of nominal prices distributed according to Benford's Law, the study showed a clear deviation from this benchmark for the second and third digits in nominal market prices with a clear trend towards psychological pricing after the nominal shock of the euro introduction.
Genome data
The number of open reading frames and their relationship to genome size differs between eukaryotes and prokaryotes with the former showing a log-linear relationship and the latter a linear relationship. Benford's law has been used to test this observation with an excellent fit to the data in both cases.
Scientific fraud detection
A test of regression coefficients in published papers showed agreement with Benford's law. As a comparison group subjects were asked to fabricate statistical estimates. The fabricated results failed to obey Benford's law.
Statistical tests
Although the chi squared test has been used to test for compliance with Benford's law it has low statistical power when used with small samples.
The Kolmogorov–Smirnov test and the Kuiper test are more powerful when the sample size is small particularly when Stephens's corrective factor is used. These tests may be overly conservative when applied to discrete distributions. Values for the Benford test have been generated by Morrow. The critical values of the test statistics are shown below:
| αTest | 0.10 | 0.05 | 0.01 |
|---|---|---|---|
| Kuiper Test | 1.191 | 1.321 | 1.579 |
| Kolmogorov–Smirnov | 1.012 | 1.148 | 1.420 |
These critical values provide the minimum test statistic values required to reject the hypothesis of compliance with Benford's law at the given significance levels.
Two alternative tests specific to this law have been published: first, the max (m) statistic is given by
and secondly, the distance (d) statistic is given by
where FSD is the First Significant Digit and N is the sample size. Morrow has determined the critical values for both these statistics, which are shown below:
| ⍺Statistic | 0.10 | 0.05 | 0.01 |
|---|---|---|---|
| Leemis' m | 0.851 | 0.967 | 1.212 |
| Cho–Gaines' d | 1.212 | 1.330 | 1.569 |
Nigrini has suggested the use of a z statistic
with
where |x| is the absolute value of x, n is the sample size, 1/2n is a continuity correction factor, pe is the proportion expected from Benford's law and po is the observed proportion in the sample.
Morrow has also shown that for any random variable X (with a continuous pdf) divided by its standard deviation (σ), a value A can be found such that the probability of the distribution of the first significant digit of the random variable (X/σ) will differ from Benford's Law by less than ε > 0. The value of A depends on the value of ε and the distribution of the random variable.
A method of accounting fraud detection based on bootstrapping and regression has been proposed.
If the goal is to conclude agreement with the Benford's law rather than disagreement, then the goodness-of-fit tests mentioned above are inappropriate. In this case the specific tests for equivalence should be applied. An empirical distribution is called equivalent to the Benford's law if a distance (for example total variation distance or the usual Euclidean distance) between the probability mass functions is sufficiently small. This method of testing with application to Benford's law is described in Ostrovski (2017).
Generalization to digits beyond the first

It is possible to extend the law to digits beyond the first. In particular, the probability of encountering a number starting with the string of digits n is given by:
For example, the probability that a number starts with the digits 3, 1, 4 is log10(1 + 1/314) ≈ 0.00138, as in the figure on the right.
This result can be used to find the probability that a particular digit occurs at a given position within a number. For instance, the probability that a "2" is encountered as the second digit is
And the probability that d (d = 0, 1, ..., 9) is encountered as the n-th (n > 1) digit is
The distribution of the n-th digit, as n increases, rapidly approaches a uniform distribution with 10% for each of the ten digits, as shown below. Four digits is often enough to assume a uniform distribution of 10% as '0' appears 10.0176% of the time in the fourth digit while '9' appears 9.9824% of the time.
| Digit | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1st | — | 30.1% | 17.6% | 12.5% | 9.7% | 7.9% | 6.7% | 5.8% | 5.1% | 4.6% |
| 2nd | 12% | 11.4% | 10.9% | 10.4% | 10% | 9.7% | 9.3% | 9% | 8.8% | 8.5% |
| 3rd | 10.2% | 10.1% | 10.1% | 10.1% | 10% | 10% | 9.9% | 9.9% | 9.9% | 9.8% |
Tests with common distributions
Benford's law was empirically tested against the numbers (up to the 10th digit) generated by a number of important distributions, including the uniform distribution, the exponential distribution, the half-normal distribution, the right-truncated normal, the normal distribution, the chi square distribution and the log normal distribution. In addition to these the ratio distribution of two uniform distributions, the ratio distribution of two exponential distributions, the ratio distribution of two half-normal distributions, the ratio distribution of two right-truncated normal distributions, the ratio distribution of two chi-square distributions (the F distribution) and the log normal distribution were tested.
The uniform distribution as might be expected does not obey Benford's law. In contrast, the ratio distribution of two uniform distributions is well described by Benford's law. Benford's law also describes the exponential distribution and the ratio distribution of two exponential distributions well. Although the half-normal distribution does not obey Benford's law, the ratio distribution of two half-normal distributions does. Neither the right-truncated normal distribution nor the ratio distribution of two right-truncated normal distributions are well described by Benford's law. This is not surprising as this distribution is weighted towards larger numbers. Neither the normal distribution nor the ratio distribution of two normal distributions (the Cauchy distribution) obey Benford's law. The fit of chi square distribution depends on the degrees of freedom (df) with good agreement with df = 1 and decreasing agreement as the df increases. The F distribution is fitted well for low degrees of freedom. With increasing dfs the fit decreases but much more slowly than the chi square distribution. The fit of the log-normal distribution depends on the mean and the variance of the distribution. The variance has a much greater effect on the fit than does the mean. Larger values of both parameters result in better agreement with the law. The ratio of two log normal distributions is a log normal so this distribution was not examined.
Other distributions that have been examined include the Muth distribution, Gompertz distribution, Weibull distribution, gamma distribution, log-logistic distribution and the exponential power distribution all of which show reasonable agreement with the law. The Gumbel distribution – a density increases with increasing value of the random variable – does not show agreement with this law.
Distributions known to obey Benford's law
Some well-known infinite integer sequences provably satisfy Benford's Law exactly (in the asymptotic limit as more and more terms of the sequence are included). Among these are the Fibonacci numbers, the factorials, the powers of 2, and the powers of almost any other number.
Likewise, some continuous processes satisfy Benford's Law exactly (in the asymptotic limit as the process continues through time). One is an exponential growth or decay process: If a quantity is exponentially increasing or decreasing in time, then the percentage of time that it has each first digit satisfies Benford's Law asymptotically (i.e. increasing accuracy as the process continues through time).
Distributions known to disobey Benford's law
Square roots and reciprocals do not obey this law. Also, Benford's law does not apply to unary systems such as tally marks. Telephone directories violate Benford's law because the numbers have a mostly fixed length and do not have the initial digit 1. Benford's law is violated by the populations of all places with population at least 2500 from five US states according to the 1960 and 1970 censuses, where only 19% began with digit 1 but 20% began with digit 2, for the simple reason that the truncation at 2500 introduces statistical bias. The terminal digits in pathology reports violate Benford's law due to rounding, and the fact that terminal digits are never expected to follow Benford's law in the first place.
Criteria for distributions expected and not expected to obey Benford's Law
A number of criteria—applicable particularly to accounting data—have been suggested where Benford's Law can be expected to apply and not to apply.
- Distributions that can be expected to obey Benford's Law
- When the mean is greater than the median and the skew is positive
- Numbers that result from mathematical combination of numbers: e.g. quantity × price
- Transaction level data: e.g. disbursements, sales
- Numbers produced when doing any multiplicative calculations with an Oughtred slide rule, since the answers naturally fall into the right logarithmic distribution.
- Distributions that would not be expected to obey Benford's Law
- Where numbers are assigned sequentially: e.g. check numbers, invoice numbers
- Where numbers are influenced by human thought: e.g. prices set by psychological thresholds ($1.99)
- Accounts with a large number of firm-specific numbers: e.g. accounts set up to record $100 refunds
- Accounts with a built-in minimum or maximum
- Where no transaction is recorded
Moments
Moments of random variables for the digits 1 to 9 following this law have been calculated:
For the first and second digit distribution these values are also known:
A table of the exact probabilities for the joint occurrence of the first two digits according to Benford's law is available, as is the population correlation between the first and second digits: ρ = 0.0561.
See also
References
- ^ Arno Berger and Theodore P Hill, Benford's Law Strikes Back: No Simple Explanation in Sight for Mathematical Gem, 2011
- Weisstein, Eric W. "Benford's Law". MathWorld, A Wolfram web resource. Retrieved 7 June 2015.
- Paul H. Kvam, Brani Vidakovic, Nonparametric Statistics with Applications to Science and Engineering, p. 158
- ^ Frank Benford (March 1938). "The law of anomalous numbers". Proc. Am. Philos. Soc. 78 (4): 551–572. JSTOR 984802. (subscription required)
- ^ Simon Newcomb (1881). "Note on the frequency of use of the different digits in natural numbers". American Journal of Mathematics. 4 (1/4). American Journal of Mathematics, Vol. 4, No. 1: 39–40. doi:10.2307/2369148. JSTOR 2369148. (subscription required)
- ^ Formann, A. K. (2010). Morris, Richard James (ed.). "The Newcomb-Benford Law in Its Relation to Some Common Distributions". PLoS ONE. 5 (5): e10541. Bibcode:2010PLoSO...510541F. doi:10.1371/journal.pone.0010541. PMC 2866333. PMID 20479878.
{{cite journal}}: CS1 maint: unflagged free DOI (link) - They should strictly be bars but are shown as lines for clarity.
- ^ Theodore P. Hill (1995). "A Statistical Derivation of the Significant-Digit Law" (PDF). Statistical Science. 10: 354–363. doi:10.1214/ss/1177009869. MR 1421567.
- ^ Steven W. Smith. "The Scientist and Engineer's Guide to Digital Signal Processing, chapter 34, Explaining Benford's Law". Retrieved 15 December 2012. (especially section 10).
- ^ Fewster, R. M. (2009). "A simple explanation of Benford's Law" (PDF). The American Statistician. 63 (1): 26–32. doi:10.1198/tast.2009.0005.
- ^ This section discusses and plots probability distributions of the logarithms of a variable. This is not the same as taking a regular probability distribution of a variable, and simply plotting it on a log scale. Instead, one multiplies the distribution by a certain function. The log scale distorts the horizontal distances, so the height has to be changed also, in order for the area under each section of the curve to remain true to the original distribution. See, for example, . Specifically: .
- Arno Berger and Theodore P Hill, Benford's Law Strikes Back: No Simple Explanation in Sight for Mathematical Gem, 2011. The authors describe this argument, but say it "still leaves open the question of why it is reasonable to assume that the logarithm of the spread, as opposed to the spread itself—or, say, the log log spread—should be large." Moreover, they say: "assuming large spread on a logarithmic scale is equivalent to assuming an approximate conformance with " (italics added), something which they say lacks a "simple explanation".
- ^ L. Pietronero; E. Tosatti; V. Tosatti; A. Vespignani (2001). "Explaining the uneven distribution of numbers in nature: the laws of Benford and Zipf" (PDF). Physica A. 293: 297–304. arXiv:cond-mat/9808305. Bibcode:2001PhyA..293..297P. doi:10.1016/S0378-4371(00)00633-6.
- Formann, A. K. (2010). The Newcomb-Benford law in its relation to some common distributions. PLoS ONE, 5, e10541.
- Theodore P. Hill (July–August 1998). "The first digit phenomenon" (PDF). American Scientist. 86 (4): 358. Bibcode:1998AmSci..86..358H. doi:10.1511/1998.4.358.
- Élise Janvresse and Thierry de la Rue (2004), "From Uniform Distributions to Benford's Law", Journal of Applied Probability, 41 1203–1210 doi:10.1239/jap/1101840566 MR2122815 preprint
- Roger S. Pinkham, On the Distribution of First Significant Digits, Ann. Math. Statist. Volume 32, Number 4 (1961), 1223-1230.
- MathWorld – Benford's Law
- Varian, Hal (1972). "Benford's Law (Letters to the Editor)". The American Statistician. 26 (3): 65. doi:10.1080/00031305.1972.10478934.
- ^ Nigrini, Mark J. (May 1999). "I've Got Your Number:How a mathematical phenomenon can help CPAs uncover fraud and other irregulaities". Journal of Accountancy.
- "From Benford to Erdös". Radio Lab. Episode 2009-10-09. 30 September 2009.
{{cite episode}}: Unknown parameter|serieslink=ignored (|series-link=suggested) (help) - Stephen Battersby Statistics hint at fraud in Iranian election New Scientist 24 June 2009
- Joseph Deckert, Mikhail Myagkov and Peter C. Ordeshook, (2010) The Irrelevance of Benford’s Law for Detecting Fraud in Elections Archived 17 May 2014 at the Wayback Machine, Caltech/MIT Voting Technology Project Working Paper No. 9
- Charles R. Tolle, Joanne L. Budzien, and Randall A. LaViolette (2000) Do dynamical systems follow Benford?s Law?, Chaos 10, 2, pp.331–336 (2000); doi:10.1063/1.166498
- Müller, Hans Christian: Greece Was Lying About Its Budget Numbers. Forbes. 12 September 2011.
- Sehity, Tarek el; Hoelzl, Erik; Kirchler, Erich (1 December 2005). "Price developments after a nominal shock: Benford's Law and psychological pricing after the euro introduction". International Journal of Research in Marketing. 22 (4): 471–480. doi:10.1016/j.ijresmar.2005.09.002.
- Friar, JL; Goldman, T; Pérez-Mercader, J (2012). "Genome sizes and the benford distribution". PLOS ONE. 7 (5): e36624. arXiv:1205.6512. Bibcode:2012PLoSO...736624F. doi:10.1371/journal.pone.0036624. PMC 3356352. PMID 22629319.
{{cite journal}}: CS1 maint: unflagged free DOI (link) - Diekmann A (2007) Not the First Digit! Using Benford's Law to detect fraudulent scientific data. J Appl Stat 34 (3) 321–329, doi:10.1080/02664760601004940
- Stephens, M. A. (1970). "Use of the Kolmogorov–Smirnov, Cramér–Von Mises and Related Statistics without Extensive Tables". Journal of the Royal Statistical Society, Series B. 32 (1): 115–122.
- ^ Morrow, J. (2010) "Benford’s Law, Families of Distributions and a test basis", UW-Madison
- ^ Leemis, L. M.; Schmeiser, B. W.; Evans, D. L. (2000). "Survival distributions satisfying Benford's Law". The American Statistician. 54 (4): 236–241. doi:10.1080/00031305.2000.10474554.
- Cho, W. K. T.; Gaines, B. J. (2007). "Breaking the (Benford) law: Statistical fraud detection in campaign finance". The American Statistician. 61 (3): 218–223. doi:10.1198/000313007X223496.
- Nigrini, M. (1996). "A taxpayer compliance application of Benford's Law". J Amer Tax Assoc. 18: 72–91.
- Suh, I. S.; Headrick, T. C.; Minaburo, S. (2011). "An effective and efficient analytic technique: A bootstrap regression procedure and Benford's Law". J Forensic & Investigative Accounting. 3 (3).
- Ostrovski, Vladimir (May 2017). "Testing equivalence of multinomial distributions". Statistics & Probability Letters. 124: 77–82. doi:10.1016/j.spl.2017.01.004. SSRN 2907258.
- ^ Theodore P. Hill, "The Significant-Digit Phenomenon", The American Mathematical Monthly, Vol. 102, No. 4, (Apr., 1995), pp. 322–327. Official web link (subscription required). Alternate, free web link.
- ^ Dümbgen, L; Leuenberger, C (2008). "Explicit bounds for the approximation error in Benford's Law". Elect Comm in Probab. 13: 99–112. arXiv:0705.4488. doi:10.1214/ECP.v13-1358.
- Washington, L. C. (1981). "Benford's Law for Fibonacci and Lucas Numbers". The Fibonacci Quarterly. 19 (2): 175–177.
- Duncan, R. L. (1967). "An Application of Uniform Distribution to the Fibonacci Numbers". The Fibonacci Quarterly. 5: 137–140.
- Sarkar, P. B. (1973). "An Observation on the Significant Digits of Binomial Coefficients and Factorials". Sankhya B. 35: 363–364.
- ^ In general, the sequence k, k, k, etc., satisfies Benford's Law exactly, under the condition that log10 k is an irrational number. This is a straightforward consequence of the equidistribution theorem.
- That the first 100 powers of 2 approximately satisfy Benford's Law is mentioned by Ralph Raimi. Raimi, Ralph A. (1976). "The First Digit Problem". American Mathematical Monthly. 83 (7): 521–538. doi:10.2307/2319349.
- ^ Raimi, Ralph A. (August–September 1976). "The first digit problem". American Mathematical Monthly. 83 (7): 521–538. doi:10.2307/2319349.
- The North American Numbering Plan uses 1 as a long distance prefix, and much of the rest of the world reserves it to begin special 3-digit numbers like 112 (emergency telephone number).
- Beer, Trevor W. (2009). "Terminal digit preference: beware of Benford's Law". J. Clin. Pathol. 62 (2): 192. doi:10.1136/jcp.2008.061721.
- Durtschi, C; Hillison, W; Pacini, C (2004). "The effective use of Benford's Law to assist in detecting fraud in accounting data". J Forensic Accounting. 5: 17–34.
- Scott, P.D.; Fasli, M. (2001) "Benford’s Law: An empirical investigation and a novel explanation". CSM Technical Report 349, Department of Computer Science, Univ. Essex
- ^ Suh, I.S.; Headrick, T.C. (2010). "A comparative analysis of the bootstrap versus traditional statistical procedures applied to digital analysis based on Benford's Law" (PDF). Journal of Forensic and Investigative Accounting. 2 (2): 144–175.
Further reading
- Arno Berger; Theodore P. Hill (2017). "What is…Benford's Law?" (PDF). Notices of the AMS. 64 (2): 132–134. doi:10.1090/noti1477.
- Arno Berger; Theodore P. Hill (2015). An Introduction to Benford's Law. Princeton University Press. ISBN 978-0-691-16306-2.
{{cite book}}: Unknown parameter|lastauthoramp=ignored (|name-list-style=suggested) (help) - Alex Ely Kossovsky. Benford's Law: Theory, the General Law of Relative Quantities, and Forensic Fraud Detection Applications, 2014, World Scientific Publishing. ISBN 978-981-4583-68-8.
- "Benford's Law – from Wolfram MathWorld". Mathworld.wolfram.com. 14 June 2012. Retrieved 26 June 2012.
- Mark J. Nigrini (2012). Benford's Law: Applications for Forensic Accounting, Auditing, and Fraud Detection. John Wiley & Sons. p. 330. ISBN 978-1-118-15285-0.
- Alessandro Gambini; et al. (2012). "Probability of digits by dividing random numbers: A ψ and ζ functions approach". Expositiones Mathematicae. 30 (4): 223–238. doi:10.1016/j.exmath.2012.03.001.
- Sehity; Hoelzl, Erik; Kirchler, Erich (2005). "Price developments after a nominal shock: Benford's Law and psychological pricing after the euro introduction". International Journal of Research in Marketing. 22 (4): 471–480. doi:10.1016/j.ijresmar.2005.09.002.
- Nicolas Gauvrit; Jean-Paul Delahaye (2011). "Scatter and regularity implies Benford's Law...and more". Zenil: Randomness through computation: some answers, more questions: 58–69. arXiv:0910.1359. Bibcode:2009arXiv0910.1359G. doi:10.1142/9789814327756_0004. ISBN 9814327751.
- Bernhard Rauch; Max Göttsche; Gernot Brähler; Stefan Engel (August 2011). "Fact and Fiction in EU-Governmental Economic Data". German Economic Review. 12 (3): 243–255. doi:10.1111/j.1468-0475.2011.00542.x.
- Wendy Cho; Brian Gaines (August 2007). "Breaking the (Benford) Law: statistical fraud detection in campaign finance". The American Statistician. 61 (3): 218–223. doi:10.1198/000313007X223496.
{{cite journal}}: Unknown parameter|lastauthoramp=ignored (|name-list-style=suggested) (help) - Geiringer, Hilda; Furlan, L. V. (1948). "The Law of Harmony in Statistics: An Investigation of the Metrical Interdependence of Social Phenomena. by L. V. Furlan". Journal of the American Statistical Association. 43 (242). American Statistical Association: 325–328. doi:10.2307/2280379. JSTOR 2280379.
External links
General audience
- Benford Online Bibliography, an online bibliographic database on Benford's Law.
- Companion website for Benford's Law by Mark Nigrini Website includes 15 data sets, 10 Excel templates, photos, documents, and other miscellaneous items related to Benford's Law
- Following Benford's Law, or Looking Out for No. 1, 1998 article from The New York Times.
- A further five numbers: number 1 and Benford's law, BBC radio segment by Simon Singh
- From Benford to Erdös, Radio segment from the Radiolab program
- Looking out for number one by Jon Walthoe, Robert Hunt and Mike Pearson, Plus Magazine, September 1999
- Video showing Benford's Law applied to Web Data (incl. Minnesota Lakes, US Census Data and Digg Statistics)
- An illustration of Benford's Law, showing first-digit distributions of various sequences evolve over time, interactive.
- Generate your own Benford numbers A script for generating random numbers compliant with Benford's Law.
- Testing Benford's Law An open source project showing Benford's Law in action against publicly available datasets.
- Testing Benford’s Law in OLAP Cubes Implementation with Microsoft Analysis Services.
- Mould, Steve. "Number 1 and Benford's Law". Numberphile. Brady Haran.
- A third of property values begin with a 1 An example of Benford's Law appearing in house price data.
- Benford's Very Strange Law - Professor John D. Barrow, lecture on Benford's Law.
- Interactive graphic: Univariate Distribution Relationships
More mathematical
- Weisstein, Eric W. "Benford's Law". MathWorld.
- Benford’s law, Zipf’s law, and the Pareto distribution by Terence Tao
- Country Data and Benford's Law, Benford's Law from Ratios of Random Numbers at Wolfram Demonstrations Project.
- Benford's Law Solved with Digital Signal Processing
- arXiv:1612.04200 - Few more Comments on Benford's Law










 .
.