| Revision as of 23:05, 7 December 2006 view sourceOne (talk | contribs)Extended confirmed users9,370 editsm Reverted edits by 24.160.161.64 (talk) to last version by Ilmari Karonen← Previous edit | Revision as of 01:52, 8 December 2006 view source 71.109.224.16 (talk) →Discoveries and inventionsNext edit → | ||
| Line 60: | Line 60: | ||
| Apart from general physics, he was also an ], and ] writes that the Roman ] ] brought two devices back to ] from the ransacked city of Syracuse. One device mapped the ] on a sphere and the other predicted the motions of the ] and the ] and the ]s (i.e., an ]). He credits ] and ] for constructing these devices. For some time this was assumed to be a legend of doubtful nature, but the discovery of the ] has changed the view of this issue, and it is indeed probable that Archimedes possessed and constructed such devices. ] of ] writes that Archimedes had written a practical book on the construction of such spheres entitled '']''. | Apart from general physics, he was also an ], and ] writes that the Roman ] ] brought two devices back to ] from the ransacked city of Syracuse. One device mapped the ] on a sphere and the other predicted the motions of the ] and the ] and the ]s (i.e., an ]). He credits ] and ] for constructing these devices. For some time this was assumed to be a legend of doubtful nature, but the discovery of the ] has changed the view of this issue, and it is indeed probable that Archimedes possessed and constructed such devices. ] of ] writes that Archimedes had written a practical book on the construction of such spheres entitled '']''. | ||
| Archimedes's works were not widely recognized, even in ]. He and his contemporaries probably constitute the peak of Greek ]. During the ] the mathematicians who could understand Archimedes's work were few and far between. Many of his works were lost when the ] was burnt (twice) and survived only in ] or ] ]s. As a result, his '']'' was lost until around ], after the ] had been carried out successfully. We can only speculate about the effect that the "method" would have had on the development of ] had it been known in the ] to the ] centuries. | Archimedes's works were not widely recognized, even in ]. He and his contemporaries probably constitute the peak of Greek ]. During the ] the mathematicians who could understand Archimedes's work were few and far between. Many of his works were lost when the ] was burnt (twice) and survived only in ] or ] ]s. As a result, his '']'' was lost until around ], after the ] had been carried out successfully. We can only speculate about the effect that the "method" would have had on the development of ] had it been known in the ] to the ] centuries. This nigga was hella maff. | ||
| ==Writings by Archimedes== | ==Writings by Archimedes== | ||
Revision as of 01:52, 8 December 2006
- For other senses of this word, see Archimedes (disambiguation).
| Archimedes of Syracuse (Greek: Ἀρχιμήδης) | |
|---|---|
| Era | Ancient philosophy |
| Region | Classical Greek philosophy |
Archimedes (Greek: Template:Polytonic; c. 287 BC – 212 BC) was a Hellenistic mathematician, physicist, engineer, astronomer, and philosopher, born on the seaport colony of Syracuse, Magna Graecia, what is now Sicily. Many consider him one of the greatest, if not the greatest, mathematicians in antiquity. Carl Friedrich Gauss, himself frequently called the most influential mathematician of all time, modestly claimed that Archimedes was one of the three epoch-making mathematicians (the others being Isaac Newton and Ferdinand Eisenstein). Apart from his fundamental theoretical contributions to maths, Archimedes also shaped the fields of physics and practical engineering, and has been called "the greatest scientist ever".
He was a relative of the Hiero monarchy, which was the ruling family of Syracuse, a seaport kingdom. King Hiero II, who was said to be Archimedes's uncle, commissioned him to design and fabricate a new class of ships for his navy, which were crucial for the preservation of the ruling class in Syracuse. Hiero had promised large caches of grain to the Romans in the north in return for peace. Faced with war when unable to present the promised amount, Hiero commissioned Archimedes to develop a large luxury/supply/war barge in order to serve the changing requirements of his navy. It is rumored that the Archimedes Screw was actually an invention of happenstance, as he needed a tool to remove bilge water. The ship, named Syracusia, after its nation, was huge, and its construction caused stupor in the Greek world.
He is credited with many inventions and discoveries, some of which we still use today, like his Archimedes screw. He was famous for his compound pulley, a system of pulleys used to lift heavy loads such as ships. He made several war machines for his patron and friend King Hiero II. He did a lot of work in geometry, which included finding the surface areas and volumes of solids accurately. The work that has made Archimedes famous is his theory of floating bodies. He laid down the laws of flotation and developed the famous Archimedes' principle.
Discoveries and inventions
Archimedes became a very popular figure as a result of his involvement in the defense of Syracuse against the Roman siege in the Second Punic War. He is reputed to have held the Romans at bay with war machines of his own design, to have been able to move a full-size ship complete with crew and cargo by pulling a single rope, and to have discovered the principles of density and buoyancy, also known as Archimedes' principle, while taking a bath. The story goes that he then took to the streets without any clothing, being so elated with his discovery that he forgot to dress, crying "Eureka!" ("I have found it!"). He has also been credited with the possible invention of the odometer during the First Punic War. One of his inventions used for military defense of Syracuse against the invading Romans was the claw of Archimedes.
It is said that he prevented one Roman attack on Syracuse by using a large array of mirrors (speculated to have been highly polished shields) to reflect sunlight onto the attacking ships causing them to catch fire. This popular legend, dubbed the "Archimedes's death ray", has been tested many times since the Renaissance and often discredited as it seemed the ships would have had to have been virtually motionless and very close to shore for them to ignite, an unlikely scenario during a battle. A group at the MIT have performed their own tests and concluded that the mirror weapon was a possibility , although later tests of their system showed it to be ineffective in conditions that more closely matched the described siege . The television show Mythbusters also took on the challenge of recreating the weapon and concluded that while it was possible to light a ship on fire, it would have to be stationary at a specified distance during the hottest part of a very bright, hot day, and would require several hundred troops carefully aiming mirrors while under attack. These unlikely conditions combined with the availability of other simpler methods, such as ballistae with flaming bolts, led the team to believe that the heat ray was far too impractical to be used, and probably just a myth.
It can be argued that even if the reflections didn't induce fire, they still could have confused, and temporarily blinded the ship crews, making it hard for them to aim and steer. Making them hot and sweaty before primary battle may have also tired them faster. The effectiveness may have simply been exaggerated.
Archimedes also has been credited with improving accuracy, range and power of the catapult.
Archimedes was killed by a Roman soldier during the sack of Syracuse during the Second Punic War, despite orders from the Roman general Marcellus that he was not to be harmed. The Greeks said that he was killed while drawing an equation in the sand; engrossed in his diagram and impatient with being interrupted, he is said to have muttered his famous last words before being slain by an enraged Roman soldier: Μη μου τους κύκλους τάραττε ("Don't disturb my circles"). The phrase is often given in Latin as "Noli turbare circulos meos" but there is no direct evidence that Archimedes ever uttered these words. This story was sometimes told to contrast the Greek high-mindedness with Roman ham-handedness; however, it should be noted that Archimedes designed the siege engines that devastated a substantial Roman invasion force, so his death may have been out of retribution .
In creativity and insight, Archimedes exceeded any other European mathematician prior to the European Renaissance. In a civilization with an awkward numeral system and a language in which "a myriad" (literally "ten thousand") meant "infinity", he invented a positional numeral system and used it to write numbers up to 10. He devised a heuristic method based on statistics to do private calculations that we would classify today as integral calculus, but then presented rigorous geometric proofs for his results. To what extent he actually had a correct version of integral calculus is debatable. He proved that the ratio of a circle's circumference to its diameter is the same as the ratio of the circle's area to the square of the radius. He did not call this ratio p but he gave a procedure to approximate it to arbitrary accuracy and gave an approximation of it as between 3 + 10/71 (approximately 3.1408) and 3 + 1/7 (approximately 3.1429). He was the first Greek mathematician to introduce mechanical curves (those traced by a moving point) as legitimate objects of study. He proved that the area enclosed by a parabola and a straight line is 4/3 the area of a triangle with equal base and height. (See the illustration below. The "base" is any secant line, not necessarily orthogonal to the parabola's axis; "the same base" means the same "horizontal" component of the length of the base; "horizontal" means orthogonal to the axis. "Height" means the length of the segment parallel to the axis from the vertex to the base. The vertex must be so placed that the two horizontal distances mentioned in the illustration are equal.)
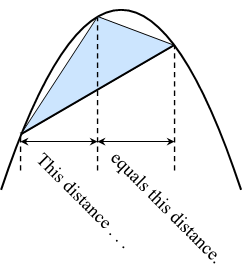
In the process, he calculated the earliest known example of a geometric progression summed to infinity with the ratio 1/4:
If the first term in this series is the area of the triangle in the illustration then the second is the sum of the areas of two triangles whose bases are the two smaller secant lines in the illustration, and so on. Archimedes also gave a quite different proof of nearly the same proposition by a method using infinitesimals (see "Archimedes' use of infinitesimals").
He proved that the area and volume of the sphere are in the same ratio to the area and volume of a circumscribed straight cylinder, a result he was so proud of that he made it his epitaph.
Archimedes is probably also the first mathematical physicist on record, and the best before Galileo and Newton. He invented the field of statics, enunciated the law of the lever, the law of equilibrium of fluids, and the law of buoyancy. He famously discovered the latter when he was asked to determine whether a wreath (often incorrectly reported as a crown -- a crown could have been melted down to determine its composition, whereas a wreath was sacred) had been made of pure gold, or gold adulterated with silver; he realized that the rise in the water level when it was immersed would be equal to the volume of the wreath, and the decrease in the weight of the wreath would be in proportion; he could then compare those with the values of an equal weight of pure gold. He was the first to identify the concept of center of gravity, and he found the centers of gravity of various geometric figures, assuming uniform density in their interiors, including triangles, paraboloids, and hemispheres. Using only ancient Greek geometry, he also gave the equilibrium positions of floating sections of paraboloids as a function of their height, a feat that would be taxing to a modern physicist using calculus.
Apart from general physics, he was also an astronomer, and Cicero writes that the Roman consul Marcellus brought two devices back to Rome from the ransacked city of Syracuse. One device mapped the sky on a sphere and the other predicted the motions of the sun and the moon and the planets (i.e., an orrery). He credits Thales and Eudoxus for constructing these devices. For some time this was assumed to be a legend of doubtful nature, but the discovery of the Antikythera mechanism has changed the view of this issue, and it is indeed probable that Archimedes possessed and constructed such devices. Pappus of Alexandria writes that Archimedes had written a practical book on the construction of such spheres entitled On Sphere-Making.
Archimedes's works were not widely recognized, even in antiquity. He and his contemporaries probably constitute the peak of Greek mathematical rigour. During the Middle Ages the mathematicians who could understand Archimedes's work were few and far between. Many of his works were lost when the library of Alexandria was burnt (twice) and survived only in Latin or Arabic translations. As a result, his mechanical method was lost until around 1900, after the arithmetization of analysis had been carried out successfully. We can only speculate about the effect that the "method" would have had on the development of calculus had it been known in the 16th to the 17th centuries. This nigga was hella maff.
Writings by Archimedes
- On the Equilibrium of Planes (2 volumes)
- This scroll explains the law of the lever and uses it to calculate the areas and centers of gravity of various geometric figures.
- On Spirals
- In this scroll, Archimedes defines what is now called Archimedes' spiral. This is the first mechanical curve (i.e., traced by a moving point) ever considered by a Greek mathematician.
- On the Sphere and The Cylinder
- In this scroll Archimedes obtains the result he was most proud of: the relation between the area of a sphere to that of a circumscribed straight cylinder is the same as that of the volume of the sphere to the volume of the cylinder (exactly 2/3).
- On Conoids and Spheroids
- In this scroll Archimedes calculates the areas and volumes of sections of cones, spheres, and paraboloids.
- On Floating Bodies (2 volumes)
- In the first part of this scroll, Archimedes spells out the law of equilibrium of fluids, and proves that water will adopt a spherical form around a center of gravity. This was probably an attempt at explaining the observation made by Greek astronomers that the Earth is round. Note that his fluids are not self-gravitating: he assumes the existence of a point towards which all things fall and derives the spherical shape. One is led to wonder what he would have done had he struck upon the idea of universal gravitation.
- In the second part, a veritable tour-de-force, he calculates the equilibrium positions of sections of paraboloids. This was probably an idealization of the shapes of ships' hulls. Some of his sections float with the base under water and the summit above water, which is reminiscent of the way icebergs float, although Archimedes probably was not thinking of this application.
- The Quadrature of the Parabola
- In this scroll, Archimedes calculates the area of a segment of a parabola (the figure delimited by a parabola and a secant line not necessarily perpendicular to the axis). The final answer is obtained by triangulating the area and summing the geometric series with ratio 1/4.
- Stomachion
- This is a Greek puzzle similar to a Tangram. In this scroll, Archimedes calculates the areas of the various pieces. This may be the first reference we have to this game. Recent discoveries indicate that Archimedes was attempting to determine how many ways the strips of paper could be assembled into the shape of a square. This is possibly the first use of combinatorics to solve a problem.
- Archimedes's Cattle Problem
- Archimedes wrote a letter to the scholars in the Library of Alexandria, who apparently had downplayed the importance of Archimedes's works. In these letters, he dares them to count the numbers of cattle in the Herd of the Sun by solving a number of simultaneous Diophantine equations, some of them quadratic (in the more complicated version). This problem is one of the famous problems solved with the aid of a computer. The solution is a very large number, approximately 7.760271×10 (See the external links to the Cattle Problem.)
- In this scroll, Archimedes counts the number of grains of sand fitting inside the universe. This book mentions Aristarchus of Samos' theory of the solar system (concluding that "this is impossible"), contemporary ideas about the size of the Earth and the distance between various celestial bodies. From the introductory letter we also learn that Archimedes's father was an astronomer.
- In this work, which was unknown in the Middle Ages, but the importance of which was realised after its discovery, Archimedes pioneers the use of infinitesimals, showing how breaking up a figure in an infinite number of infinitely small parts could be used to determine its area or volume. Archimedes probably considered these methods not mathematically precise, and he used these methods to find at least some of the areas or volumes he sought, and then used the more traditional method of exhaustion to prove them. Some details can be found at how Archimedes used infinitesimals.
See also
- Archimedes Palimpsest
- How Archimedes used infinitesimals
- The Archimedes crater on the Moon which was named in his honor.
Notes
- "Archimedes (287-212 B.C.), Greatest Scientist Ever" [[Jürgen Schmidhuber|by J. Schmidhuber]]". Retrieved October 11.
{{cite web}}: Check date values in:|accessdate=(help); URL–wikilink conflict (help); Unknown parameter|accessyear=ignored (|access-date=suggested) (help) - Athenaeus, Deipnosophistae, v, 207b.
- Eminent scientists, Published by scholastic India pvt. Ltd.
- Episode 55: Steam Cannon/Breakfast Cereal
References
- E. J. Dijksterhuis, Archimedes, 1987, Princeton University Press, Princeton, ISBN 0-691-08421-1. Republished translation of the 1938 study of Archimedes and his works by an historian of science
- Fred S. Kliner Christin J. Mamiya, "Gardener's Art Through the Ages" twelfth ed. Vol II 2005, Thompson Wadsworth- Los Angeles
External links
- Archimedes' Book of Lemmas at cut-the-knot
- Archimedes and the Rhombicuboctahedron by Antonio Gutierrez from Geometry Step by Step from the Land of the Incas.
- Archimedes Home Page
- O'Connor, John J.; Robertson, Edmund F., "Archimedes", MacTutor History of Mathematics Archive, University of St Andrews
- The Archimedes Palimpsest web pages at the Walters Art Museum.
- NOVA program on Archimedes Palimpsest
- The Archimedes Palimpsest project at The Walters Art Museum in Baltimore, Maryland
- Archimedes - The Golden Crown points out that in reality Archimedes may well have used a more subtle method than the one in the classic version of the story.
- Archimedes' Quadrature Of The Parabola Translated by Thomas Heath.
- Archimedes' On The Measurement Of The Circle Translated by Thomas Heath.
- The Works Of Archimedes by Thomas Heath.
- Archimedes' Cattle Problem
- Archimedes' Cattle Problem
- Works by Archimedes at Project Gutenberg
- Angle Trisection by Archimedes of Syracuse (Java)
- Archimedes'Triangle (Java)
- An ancient extra-geometric proof
- Archimedes' Squaring of Parabola (Java) at cut-the-knot
- Archimedes and his Burning Mirrors, Reality or Fantasy?
- Biography of Archimedes
- Squaring the circle History Topic at MacTutor
- Archimedes
- 287 BC births
- 212 BC deaths
- Natives of Syracuse
- Ancient Greek engineers
- Ancient Greek inventors
- Ancient Greek mathematicians
- Ancient Greek physicists
- Dynamicists
- Hellenistic philosophers
- Sicilian Greeks
- Sicilian mathematicians
- Sicilian scientists
- Murdered scientists
- Geometers
- Greek murder victims
- People with craters of the Moon named after them
