| Revision as of 02:03, 29 May 2005 editEms57fcva (talk | contribs)Extended confirmed users5,831 editsm →History: - corrected 2nd occurance of previous typo← Previous edit | Revision as of 23:36, 29 May 2005 edit undoHillman (talk | contribs)11,881 edits →Textbooks: Added more fine textbooks and converted citations to standard template.Next edit → | ||
| Line 136: | Line 136: | ||
| ===Textbooks=== | ===Textbooks=== | ||
| *Bernard F. Schutz, ''A First Course in General Relativity'', Cambridge University Press (2003). This book focuses on the key mathematical building block of relativity: ]. Schutz assumes a solid knowledge on vectors and calculus. | |||
| This reading list is loosely based on | |||
| *Carroll, Sean M., '''', Addison Wesley, San Francisco (]). ISBN 0-8053-8732-3. A modern graduate level textbook. | |||
| {{Web reference | title=A Guide to Books on Relativity Theory | work=Relativity on the World Wide Web | URL=http://math.ucr.edu/home/baez/RelWWW/reading.html | date=May 29 | year=2005}} | |||
| *Robert M. Wald, ''General Relativity'', University Of Chicago Press (1984). A valuable reference for GR. The book contains a very good treatment of energy in GR, Killing vector fields, and ADM energy-momentum. | |||
| *D'Inverno, Ray, ''Introducing Einstein's Relativity'', Oxford University Ass Press (]). A modern undergraduate level text. | |||
| ==== Introductory ==== | |||
| *Misner, Charles, ], and ], ''Gravitation'', Freeman (]). ISBN 0716703440. A classic graduate level text book, which, if somewhat long winded, pays more attention to the geometrical basis and the development of ideas in general relativity than some other approaches. | |||
| * {{Book reference | Author=Hughston, L. & Tod, K. P. | Title=Introduction to General Relativity | Publisher=Cambridge: Cambridge University Press | Year=1991 | ID=ISBN 0-521-33943-X}} Clearly written, short and sweet; covers less ground than the others but much cheaper. | |||
| * {{Book reference | Author=d'Inverno, Ray | Title=Introducing Einstein's Relativity | Publisher=Oxford: Oxford University Press | Year=1992 | ID=ISBN 0-19-859686-3}} Readable, well illustrated, fairly comprehensive without becoming encyclopedic--- what's not to love? | |||
| *{{Book reference | Author=Schutz, Bernard F. | Title=A First Course in General Relativity | Publisher=Cambridge: Cambridge University Press | Year=1985 | ID=ISBN 0-521-27703-5}} Features an outstanding treatment of ] and the ], a key topic which beginners often have trouble grasping. The treatment of linearized ] and ] is also outstanding. | |||
| * {{Book reference | Author=Carroll, Sean M. | Title=Spacetime and Geometry: An Introduction to General Relativity | Publisher=San Francisco: Addison-Wesley | Year = 2004 | ID=ISBN 0-8053-8732-3}} Readable, up-to-date. Features an outstanding treatment of the ], ], and ] of isolated objects, plus an elementary introduction to ] on curved spacetimes and Hawking radiation. Further essential material is concisely explained in valuable appendices. | |||
| * {{Book reference | Author=Stephani, Hans | Title=General Relativity: An Introduction to the Theory of the Gravitational Field, | Publisher=Cambridge: Cambridge University Press | Year=1990 | ID=ISBN 0-521-37941-5}} Clear and very well organized. Features excellent treatment of ] and ] expansions and linearized ], including ]. Offers more on solution techniques than other introductory textbooks. | |||
| * {{Book reference | Author=Ohanian, Hans C. & Ruffini, Remo | Title=Gravitation and Spacetime | Publisher= New York: W. W. Norton| Year=1994 | ID=0-393-96501-5}} In contrast to other introductions, these authors use an exceptionally clear comparision of ] with ] to motivate ]. Superb treatment of observational tests and of gravitational lensing. Should be useful for students wishing to master the textbook by Weinberg. | |||
| ==== Advanced ==== | |||
| * {{Book reference | Author=Landau, L. D. & Lifschitz, E. F. | Title=The Classical Theory of Fields | Publisher=London: Butterworth-Heinemann | Year=1980 | ID=ISBN 0-7506-2768-9}} A unique texbook straddling the modern and pre-modern eras in general relativity, this offers a dual introduction to Maxwell's theory of electromagnetism and Einstein's theory of gravitation. Noteworthy topics include a good treatment of multipole moments and background material needed for the ]. | |||
| * {{Book reference | Author=Misner, Charles; Thorne, Kip S. & Wheeler, John Archibald | Title=Gravitation | Publisher=San Francisco: W. H. Freeman | Year=1973 | ID=ISBN 0-7167-0344-0}} The first modern gtr textbook. Forty-four chapters of pure joy, affectionately known as ''the phone book''. Features a unique two-track organization, with numerous boxes, tables, figures, and citations. | |||
| * {{Book reference | Author=Weinberg, Steven | Title=Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity | Publisher=New York: John Wiley & Sons | Year=1972}} Demanding but full of valuable insight and techniques. No pictures, in marked contrast to the textbook by Misner, Thorne & Wheeler. Excellent treatment of topics related to PPN formalism, weak field approximations, gravitons, as well as applications of particle physics to cosmology. No exercises. | |||
| * {{Book reference | Author=Wald, Robert M. | Title=General Relativity | Publisher=Chicago: University of Chicago Press | Year = 1984 | ID=ISBN 0-226-87033-2}} Often cited as the definitive graduate level textbook. Features an outstanding introduction to tensors (with a clear distinction between ''abstract indices'' and particular indices, overlooked by most other authors), as well as the basic singularity, stability, and uniqueness theorems, quantum field theory on curved spacetimes, and black hole thermodynamics. Much valuable material is clearly explained in a series of superb appendices. In general, this book focuses more on developing insight into mathematical formalism and techniques than on developing physical insight. | |||
| ==== Special Topics ==== | |||
| * {{Book reference | Author=Lightman, Alan P.; Press, William H. & Teukolsky, Saul A. | Title=Problem Book in Relativity and Gravitation | Publisher=Princeton: Princeton University Press | Year=1975 | ID=ISBN 0-691-08162-X}} A collection of excellent problems, with sketch solutions in the back. Text your skills! | |||
| * {{Book reference | Author=Poisson, Eric | Title=A Relativist's Toolkit: The Mathematics of Black Hole Mechanics | Publisher=Cambridge: Cambridge University Press | Year=2004 | ID=ISBN 0-521-83091-5}} Don't be fooled by the subtitle; this book explains many key concepts and techniques which are needed by ''all'' contemporary graduate students, but are not adequately explained elsewhere. Essential topics covered here include ] (expansion, vorticity, and shear), ], ] for matching ] to ], ] (including null shells), ], and ]. | |||
| * {{Book reference | Author=Stewart, John | Title=Advanced General Relativity | Publisher=Cambridge: Cambridge University Press | Year=1993 | ID=ISBN 0-521-44946-4}} Not easy to read, but one of the few textbooks to offer an introduction to the important ]. Also features much material on gravitational waves. | |||
| * {{Book reference | Author=De Felice, F. & Clarke, C. J. | Title=Relativity on Curved Manifolds | Publisher=Cambridge: Cambridge University Press| Year=1992 | ID=ISBN 0-521-42908-0}} This book is billed as an introductory textbook, but has no exercises and may be hard to read. Unique features include a chapter on ] for general relativity, plus an introduction to ] formalism. | |||
| ===Online notes and courses=== | ===Online notes and courses=== | ||
Revision as of 23:36, 29 May 2005
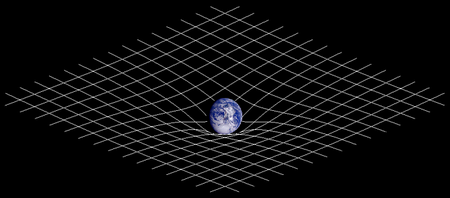
General relativity (GR) or general relativity theory (GRT) is a fundamental physical theory of gravitation which corrects and extends Newtonian gravitation, especially at the macroscopic level of stars or planets.
General relativity may be regarded as an extension of special relativity, this latter theory correcting Newtonian mechanics at high velocities. General relativity has a unique role amongst physical theories in the sense that it interprets the gravitational field as a geometric phenomenon. More specifically, it assumes that any object possessing mass curves the 'space' in which it exists, this curvature being equated to gravity. To conceptualize this equivalence, it is helpful to think, as several author-physicists have suggested, in terms of gravity not causing or being caused by spacetime curvature, but rather that gravity is spacetime curvature. It deals with the motion of bodies in such 'curved spaces' and has survived every experimental test performed on it since its formulation by Albert Einstein in 1915.
General relativity forms the basis for modern studies in fields such as astronomy, cosmology and astrophysics. It describes with great accuracy and precision many phenomena where classical physics fails, such as the perihelion motion of planets (classical physics cannot fully account for the perihelion shift of Mercury, for example) and the bending of starlight by the Sun (again, classical physics can only account for half the experimentally observed bending). It also predicts phenomena such as the existence of gravitational waves, black holes and the expansion of the universe. In fact, even Einstein himself initially believed that the universe cannot be expanding, but experimental observations of distant galaxies by Edwin Hubble finally forced Einstein to concede.
Unlike the other revolutionary physical theory, quantum mechanics, general relativity was essentially formulated by one man - Albert Einstein. However, Einstein required the help of one of his friends, Marcel Grossmann, to help him with the mathematics of curved manifolds.
Physical Description of the Theory
In relativity theory, physical phenomena are described by observers making measurements in reference frames. In general relativity, these reference frames are arbitrarily moving relative to each other (unlike in special relativity, where the reference frames are assumed to be inertial).
Consider two such reference frames, for example, one situated on Earth (the 'Earth-frame'), and another in orbit around the Earth (the 'orbit-frame'). An observer (O) in the orbit-frame will feel weightless as they 'fall' towards the Earth.
In Newtonian gravitation, O's motion is explained by the action at a distance formulation of gravity, where it is assumed that a force between the Earth and O causes O to move around the Earth.
General relativity views the situation in a different manner, namely, by demonstrating that the Earth modifies ('warps') the geometry in its vicinity and O will naturally follow the curves (geodesics) in this geometry unless O applies accelerative force (e.g. rockets). More precisely, the presence of matter determines the geometry of spacetime, the physical arena in which all events take place. This is a profound innovation in physics, all other physical theories assuming the structure of the spacetime in advance. It is important to note that a given matter distribution will fix the spacetime once and for all. There are a few caveats here: (1) the spacetime within which the matter is distributed cannot be properly defined without the matter, so most solutions require special assumptions, such as symmetries, to allow the relativist to concoct a candidate spacetime, then see where the matter must lie, then require its properties be "reasonable" and so on. (2) Initial and boundary conditions can also be a problem, so that gravitational waves may violate the idea of the spacetime being fixed once and for all.
The motion of the observer O in orbit is rather like a ping-pong ball being forced to follow the 'dent' or depression created in a trampoline by a relatively massive object like a medicine ball. The geometry is determined by the medicine ball, the relatively light ping-pong ball causing no significant change in the local geometry. Thus, general relativity provides a simpler and more natural description of gravity than Newton's action at a distance formulation. An oft-quoted analogy used in visualising spacetime curvature is to imagine a universe of one-dimensional beings living in one dimension of space and one dimension of time. Each piece of matter is not a point on any imaginable curved surface, but a world line showing where that point moves as it goes from the past to the future.
The precise means of calculating the geometry of spacetime given the matter distribution is encapsulated in Einstein's field equation.
The Equivalence Principle
- (For more detailed information about the equivalence principle, see equivalence principle)
Inertial reference frames, in which bodies maintain a uniform state of motion unless acted upon by another body, are distinguished from non-inertial frames, in which freely moving bodies have an acceleration deriving from the reference frame itself.
In non-inertial frames there is a perceived force which is accounted for by the acceleration of the frame, not by the direct influence of other matter. Thus we feel acceleration when cornering on the roads when we use a car as the physical base of our reference frame. Similarly there are coriolis and centrifugal forces when we define reference frames based on rotating matter (such as the Earth or a child's roundabout). In Newtonian mechanics, the coriolis and centrifugal forces are regarded as non-physical ones, arising from the use of a rotating reference frame. In General Relativity there is no way, locally, to define these "forces" as distinct from those arising through the use of any non-inertial reference frame.
The principle of equivalence in general relativity states that there is no local experiment to distinguish non-rotating free fall in a gravitational field from uniform motion in the absence of a gravitational field.
In short there is no gravity in a reference frame in free fall. From this perspective the observed gravity at the surface of the Earth is the force observed in a reference frame defined from matter at the surface which is not free, but is acted on from below by the matter within the Earth, and is analogous to the acceleration felt in a car.
In the process of discovering GR, Einstein used a fact that was known since the time of Galileo, namely, that the inertial and gravitational masses of an object happen to be the same. He used this as the basis for the principle of equivalence, which describes the effects of gravitation and acceleration as different perspectives of the same thing (at least locally), and which he stated in 1907 as:
- We shall therefore assume the complete physical equivalence of a gravitational field and the corresponding acceleration of the reference frame. This assumption extends the principle of relativity to the case of uniformly accelerated motion of the reference frame.
In other words, he postulated that no experiment can locally distinguish between a uniform gravitational field and a uniform acceleration. The meaning of the Principle of Equivalence has gradually broadened, in consonance with Einstein's further writings, to include the concept that no physical measurement within a given unaccelerated reference system can determine its state of motion. This implies that it is impossible to measure, and therefore virtually meaningless to discuss, changes in fundamental physical constants, such as the rest masses or electrical charges of elementary particles in different states of relative motion. Any measured change in such a constant would represent either experimental error or a demonstration that the theory of relativity was wrong or incomplete.
The equivalence principle explains the experimental observation that inertial and gravitational mass are equivalent. Moreover, the principle implies that some frames of reference must obey a non-Euclidean geometry: that spacetime is curved (by matter and energy), and gravity can be seen purely as a result of this geometry. This yields many predictions such as gravitational redshifts and light bending around stars, black holes, time slowed by gravitational fields, and slightly modified laws of gravitation even in weak gravitational fields. However, it should be noted that the equivalence principle does not uniquely determine the field equations of curved spacetime, and there is a parameter known as the cosmological constant which can be adjusted.
The Covariance Principle
Following on from the spirit of special relativity, the principle of general covariance states that all coordinate systems are equivalent for the formulation of the general laws of nature. Mathematically, this suggests that the laws of physics should be tensor equations.
Foundations
General relativity's mathematical foundations go back to the axioms of Euclidean geometry and the many attempts over the centuries to prove Euclid's fifth postulate, that parallel lines remain always equidistant, culminating with the realisation by Lobachevsky, Bolyai and Gauss that this postulate need not be true. It is an eternal monument to Euclid's genius that he classified this principle as a postulate and not as an axiom. The general mathematics of non-Euclidean geometries was developed by Gauss' student, Riemann, but these were thought to be mostly inapplicable to the real world until Einstein developed his theory of relativity. The existing applications were restricted to the geometry of curved surfaces in Euclidean space, as if one lived and moved in such a surface, and to the mechanics of deformable bodies. While such applications seem trivial compared to the calculations in the four dimensional spacetimes of general relativity, they provided a minimal development and test environment for some of the equations.
Gauss had realised that there is no a priori reason for the geometry of space to be Euclidean. This means that if a physicist holds up a stick, and a cartographer stands some distance away and measures its length by a triangulation technique based on Euclidean geometry, then he is not guaranteed to get the same answer as if the physicist brings the stick to him and he measures its length directly. Of course, for a stick he could not in practice measure the difference between the two measurements, but there are equivalent measurements which do detect the non-Euclidean geometry of space-time directly; for example the Pound-Rebka experiment (1959) detected the change in wavelength of light from a cobalt source rising 22.5 meters against gravity in a shaft in the Jefferson Physical Laboratory at Harvard, and the rate of atomic clocks in GPS satellites orbiting the Earth has to be corrected for the effect of gravity.
Newton's theory of gravity had assumed that objects had absolute velocities: that some things really were at rest while others really were in motion. He realized, and made clear, that there was no way these absolutes could be measured. All the measurements one can make provide only velocities relative to one's own velocity (positions relative to one's own position, and so forth), and all the laws of mechanics would appear to operate identically no matter how one was moving. Newton believed, however, that the theory could not be made sense of without presupposing that there are absolute values, even if they cannot be experimental error or a demonstration that the theory of relativity was wrong or incomplete.
Predictions of GR
- (For more detailed information about tests and predictions of general relativity, see Tests of general relativity)
Like any good scientific theory, general relativity makes predictions which can be tested. Some of the predictions of general relativity include the perihelion shifts of planetary orbits (particularly that of Mercury (planet)), bending of light by massive objects, and the existence of gravitational waves. The first two of these tests have been verified to a high degree of accuracy and precision. Most researchers believe in the existence of gravitational waves, but more accurate experiments are needed to raise this prediction to the status of the other two, if one demands direct detection of the waves. Nevertheless, indirect effects of gravitational wave emission have been observed for a binary system of orbiting neutron stars, as described in Tests of general relativity.
Other predictions include the expansion of the universe, the existence of black holes and possibly the existence of wormholes. The existence of black holes is generally accepted, but the existence of wormholes is still very controversial, many researchers believing that wormholes may exist only in the presence of exotic matter. The existence of white holes is very speculative, as they appear to contradict the second law of thermodynamics.
Many other quantitative predictions of general relativity have since been confirmed by astronomical observations. One of the most recent, the discovery in 2003 of PSR J0737-3039, a binary neutron star in which one component is a pulsar and where the perihelion precesses 16.88° per year (or about 140,000 times faster than the precession of Mercury's perihelion), enabled the most precise experimental verification yet of the effects predicted by general relativity. .
Mathematics of GR
- (For more detailed information about the mathematics of general relativity, see mathematics of general relativity)
The idea of curvature can be clarified by the following considerations. While it can be helpful for visualization to imagine a curved surface sitting in a space of higher dimension, this model is not very useful for the real universe; although a two dimensional surface can be embedded in three, and thus visualized well, a curved four dimensional spacetime such as our universe cannot be imbedded in a flat space of even five dimensions, but many more are required. Curvature can be measured entirely within a surface, and similarly within a higher-dimensional manifold such as space or spacetime. On Earth, if you start at the North Pole, walk south for about 10,000 km (to the Equator), turn left by 90 degrees, walk for 10,000 more km, and then do the same again (walk for 10,000 more km, turn left by 90 degrees, walk for 10,000 more km), you will be back where you started. Such a triangle with three right angles is only possible because the surface of the earth is curved. The curvature of spacetime can be evaluated, and indeed given meaning, in a similar way. Curvature may be quantified by the Riemann tensor, essentially a matrix of numbers which describes how a vector that is moved along a curve parallel to itself changes when a round trip is made. In flat space, the vector returns to the same orientation, but in a curved space it generally does not. In spaces of two dimensions, the Riemann tensor is a matrix (i.e., just a number) called the Gaussian or scalar curvature.
Relationship to other physical theories
Special and general relativity
In relativity theory, all events are referred to a reference frame. A reference frame is defined by choosing particular matter as the basis for its definition. Thus, all motion is defined and quantified relative to other matter. In the special theory of relativity it is assumed that reference frames can be extended indefinitely in all directions in space and time. The theory of special relativity concerns itself with reference frames that move at a constant velocity with respect to each other (i.e. inertial reference frames), whereas general relativity deals with all frames of reference. In the general theory it is recognised that we can only define local frames to given accuracy for finite time periods and finite regions of space (similarly we can draw flat maps of regions of the surface of the earth but we cannot extend them to cover the whole surface without distortion). In general relativity Newton's laws are assumed to hold in locally inertial reference frames.
The special theory of relativity (1905) modified the equations used in comparing the measurements made by differently moving bodies, in view of the constant value of the speed of light, i.e. its observed invariance in reference frames moving uniformly relative to each other. This had the consequence that physics could no longer treat space and time separately, but only as a single four-dimensional system, "space-time," which was divided into "time-like" and "space-like" directions differently depending on the observer's motion. The general theory added to this that the presence of matter "warped" the local space-time environment, so that apparently "straight" lines through space and time have the properties we think of "curved" lines as having.
Thus Newton's first law is replaced by the law of geodesic motion.
There are no known experimental results that suggest that a theory of gravity radically different from general relativity is necessary. For example, the Allais effect was initially speculated to demonstrate "gravitational shielding," but was subsequently explained by conventional phenomena.
Quantum mechanics and general relativity
There are good theoretical reasons for considering general relativity to be incomplete. General relativity does not include quantum mechanics, and this causes the theory to break down at sufficiently high energies. A continuing unsolved challenge of modern physics is the question of how to correctly combine general relativity with quantum mechanics, thus applying it also to the smallest scales of time and space.
Other theories
The Brans-Dicke theory and the Rosen bi-metric theory are modifications of general relativity and cannot be ruled out by current experiments.
There have been attempts to formulate consistent theories which combine gravity and electromagnetism, some of the first being the Kaluza-Klein theory and Weyl's gauge theory.
Nonlinearity of the field equations
The field equations of general relativity are a set of nonlinear partial differential equations for the metric. As such, this distinguishes the field equations of general relativity from some of the other important field equations in physics, such as Maxwell's equations (which are linear in the electric and magnetic fields) and Schrodinger's equation (which is linear in the wavefunction).
History
Full article: The development of general relativity
See also: Tests of general relativity
The development of general relativity began in 1907 with the publication of an article by Einstein on acceleration under special relativity. In that article, he argued that free fall is really inertial motion, and that for a freefalling observer the rules of special relativity must apply. This argument is called the Equivalence principle. Einstein also predicted the existance of gravitational time dilation in the 1907 article. In 1911, Einstein published another article expanding on the 1907 article, in which additional effects such as the deflection of light by massive bodies were predicted.
By 1912, Einstein was actively seeking a theory in which gravitation was explained as a geometric phenomenon. At the urging of Levi-Civita, Einstein started by exploring the use of general covariance (which is essentially the use of curvature tensors) to create a gravitational theory. However, in 1913 Einstein abandoned that approach, arguing that it is inconsistent based on the "hole argument". In 1914 and much of 1915, Einstein was trying to create field equations based on another approach. When that approach was proven to be inconsistent, Einstein revisited the concept of general covariance and discovered that the hole argument was flawed. Realizing that general covariance was tenable, Einstein quickly completed the development of the field equations that are named after him.
In this final phase, Einstein made one famous goof. In October of 1914, Einstein published field equations that were
.
These field equations predicted the non-Newtonian perihelion precession of Mercury, and so had Einstein very excited. However, it was soon realized that they were inconsistent with the local conservation of energy-momentum unless the universe had of a constant density of mass-energy-momentum. In other words, air, rock, and even vacuum should all have the same density! This inconsistency with observation sent Einstein back to the drawing board. However, the solution was all but obvious, and in November of 1915 Einstein published the actual Einstein field equations:
.
With the publication of the field equations, the issue became one of solving them for various cases and interpreting the solutions. This and experimental verification have dominated general relativity research ever since.
Since the field equations are non-linear, Einstein assumed that they were insolvable. He was disabused of this notion in 1916, when Karl Schwarzschild sent him an exact solution for the case of a spherically symmetric spacetime surrounding a massive object in spherical coordinates. This is now known as the Schwarzschild solution. Since then many other exact solutions have been found.
The expansion of the universe created an interesting episode for general relativity. In 1922, Alexander Friedmann found a solution in which the universe may expand or contract, and later Georges Lemaître derived a solution for an expanding universe. Einstein did not believe in an expanding universe, and so he once again edited the field equations, adding in a cosmological constant Λ. The revised field equations were
.
This permitted the creation of steady-state solutions, but they were notorious for being unstable: the slightest deviation from an ideal state would still result in the universe expanding or contracting. In 1929, Edwin Hubble found evidence for the idea that the universe is expanding. This resulted in Einstein dropping the Cosmological constant, referring to it as "the biggest blunder in my career".
Progress in solving the field equations and understanding the solutions has been ongoing. The solution for a spherically symmetric charged object was discovered by Reissner and later rediscovered by Nordström, and is called the Reissner-Nordström solution. The black hole aspect of the Schwarzschild solution was very controversial, and Einstein did not beleive it. However, in 1957 (two years after Einstein's death in 1955), Kruskal published a proof that black holes are called for by the Schwarzschild Solution. Additionally, the solution for a rotating massive object was obtained by Kerr in the 1960's as is called the Kerr solution. The Kerr-Newman solution for a rotating, charged massive object was published a few years later.
Observationally, general relativity has a history too. The perihelion precession of Mercury was the first evidence that general relativity is correct. Eddington's 1919 expedition in which he confirmed Einstein's prediction for the deflection of light by the Sun helped to cement the status of general relativity as a likely true theory. Since then many observations have confirmed the correctness of general relativity. These include studies of binary pulsars, observations of radio signals passing the limb of the Sun, and even the GPS system. For more information, see the Tests of general relativity article.
Finally, there have been various attempts through the years to find modifications to general relativity. The most famous of these are the Brans-Dicke theory (also known as scalar-tensor theory), and Rosen's bimetric theory. Both of these proposed changes to the field equations, and both have been found to be in conflict with observation. In fact, the viability of any approach that changes the field equations is doubtful due to a proof published in the 1990s that only the Einstein Field Equations can provide both self-consistency and local consistency with special relativity. However, general relativity is known to be inconsistent with quantum mechanics, a theory which has been better verified than general relativity. So speculation continues that some modification of general relativity is needed.
Quotes
- The theory appeared to me then, and still does, the greatest feat of human thinking about nature, the most amazing combination of philosophical penetration, physical intuition, and mathematical skill. But its connections with experience were slender. It appealed to me like a great work of art, to be enjoyed and admired from a distance. —Max Born
References
Textbooks
This reading list is loosely based on
"A Guide to Books on Relativity Theory". Relativity on the World Wide Web. May 29. {{cite web}}: Check date values in: |date= and |year= / |date= mismatch (help)
Introductory
- . ISBN 0-521-33943-X.
{{cite book}}: Missing or empty|title=(help); Unknown parameter|Author=ignored (|author=suggested) (help); Unknown parameter|Publisher=ignored (|publisher=suggested) (help); Unknown parameter|Title=ignored (|title=suggested) (help); Unknown parameter|Year=ignored (|year=suggested) (help) Clearly written, short and sweet; covers less ground than the others but much cheaper.
- . ISBN 0-19-859686-3.
{{cite book}}: Missing or empty|title=(help); Unknown parameter|Author=ignored (|author=suggested) (help); Unknown parameter|Publisher=ignored (|publisher=suggested) (help); Unknown parameter|Title=ignored (|title=suggested) (help); Unknown parameter|Year=ignored (|year=suggested) (help) Readable, well illustrated, fairly comprehensive without becoming encyclopedic--- what's not to love?
- . ISBN 0-521-27703-5.
{{cite book}}: Missing or empty|title=(help); Unknown parameter|Author=ignored (|author=suggested) (help); Unknown parameter|Publisher=ignored (|publisher=suggested) (help); Unknown parameter|Title=ignored (|title=suggested) (help); Unknown parameter|Year=ignored (|year=suggested) (help) Features an outstanding treatment of tensor calculus and the matter tensor, a key topic which beginners often have trouble grasping. The treatment of linearized gravitational waves and stellar models is also outstanding.
- . ISBN 0-8053-8732-3.
{{cite book}}: Missing or empty|title=(help); Unknown parameter|Author=ignored (|author=suggested) (help); Unknown parameter|Publisher=ignored (|publisher=suggested) (help); Unknown parameter|Title=ignored (|title=suggested) (help); Unknown parameter|Year=ignored (|year=suggested) (help) Readable, up-to-date. Features an outstanding treatment of the mass, charge, and spin of isolated objects, plus an elementary introduction to quantum field theory on curved spacetimes and Hawking radiation. Further essential material is concisely explained in valuable appendices.
- . ISBN 0-521-37941-5.
{{cite book}}: Missing or empty|title=(help); Unknown parameter|Author=ignored (|author=suggested) (help); Unknown parameter|Publisher=ignored (|publisher=suggested) (help); Unknown parameter|Title=ignored (|title=suggested) (help); Unknown parameter|Year=ignored (|year=suggested) (help)CS1 maint: extra punctuation (link) Clear and very well organized. Features excellent treatment of far-field and weak-field expansions and linearized gravitational waves, including multipole moments. Offers more on solution techniques than other introductory textbooks.
- . 0-393-96501-5.
{{cite book}}: Missing or empty|title=(help); Unknown parameter|Author=ignored (|author=suggested) (help); Unknown parameter|Publisher=ignored (|publisher=suggested) (help); Unknown parameter|Title=ignored (|title=suggested) (help); Unknown parameter|Year=ignored (|year=suggested) (help) In contrast to other introductions, these authors use an exceptionally clear comparision of linearized general relativity with electromagnetism to motivate Einstein's field equations. Superb treatment of observational tests and of gravitational lensing. Should be useful for students wishing to master the textbook by Weinberg.
Advanced
- . ISBN 0-7506-2768-9.
{{cite book}}: Missing or empty|title=(help); Unknown parameter|Author=ignored (|author=suggested) (help); Unknown parameter|Publisher=ignored (|publisher=suggested) (help); Unknown parameter|Title=ignored (|title=suggested) (help); Unknown parameter|Year=ignored (|year=suggested) (help) A unique texbook straddling the modern and pre-modern eras in general relativity, this offers a dual introduction to Maxwell's theory of electromagnetism and Einstein's theory of gravitation. Noteworthy topics include a good treatment of multipole moments and background material needed for the BKL conjecture.
- . ISBN 0-7167-0344-0.
{{cite book}}: Missing or empty|title=(help); Unknown parameter|Author=ignored (|author=suggested) (help); Unknown parameter|Publisher=ignored (|publisher=suggested) (help); Unknown parameter|Title=ignored (|title=suggested) (help); Unknown parameter|Year=ignored (|year=suggested) (help) The first modern gtr textbook. Forty-four chapters of pure joy, affectionately known as the phone book. Features a unique two-track organization, with numerous boxes, tables, figures, and citations.
-
{{cite book}}: Empty citation (help) Demanding but full of valuable insight and techniques. No pictures, in marked contrast to the textbook by Misner, Thorne & Wheeler. Excellent treatment of topics related to PPN formalism, weak field approximations, gravitons, as well as applications of particle physics to cosmology. No exercises.
- . ISBN 0-226-87033-2.
{{cite book}}: Missing or empty|title=(help); Unknown parameter|Author=ignored (|author=suggested) (help); Unknown parameter|Publisher=ignored (|publisher=suggested) (help); Unknown parameter|Title=ignored (|title=suggested) (help); Unknown parameter|Year=ignored (|year=suggested) (help) Often cited as the definitive graduate level textbook. Features an outstanding introduction to tensors (with a clear distinction between abstract indices and particular indices, overlooked by most other authors), as well as the basic singularity, stability, and uniqueness theorems, quantum field theory on curved spacetimes, and black hole thermodynamics. Much valuable material is clearly explained in a series of superb appendices. In general, this book focuses more on developing insight into mathematical formalism and techniques than on developing physical insight.
Special Topics
- . ISBN 0-691-08162-X.
{{cite book}}: Missing or empty|title=(help); Unknown parameter|Author=ignored (|author=suggested) (help); Unknown parameter|Publisher=ignored (|publisher=suggested) (help); Unknown parameter|Title=ignored (|title=suggested) (help); Unknown parameter|Year=ignored (|year=suggested) (help) A collection of excellent problems, with sketch solutions in the back. Text your skills!
- . ISBN 0-521-83091-5.
{{cite book}}: Missing or empty|title=(help); Unknown parameter|Author=ignored (|author=suggested) (help); Unknown parameter|Publisher=ignored (|publisher=suggested) (help); Unknown parameter|Title=ignored (|title=suggested) (help); Unknown parameter|Year=ignored (|year=suggested) (help) Don't be fooled by the subtitle; this book explains many key concepts and techniques which are needed by all contemporary graduate students, but are not adequately explained elsewhere. Essential topics covered here include congruences (expansion, vorticity, and shear), optical scalars, junction conditions for matching interior solutions to exterior solutions, thin shells (including null shells), spatial hyperslices, and energy conditions.
- . ISBN 0-521-44946-4.
{{cite book}}: Missing or empty|title=(help); Unknown parameter|Author=ignored (|author=suggested) (help); Unknown parameter|Publisher=ignored (|publisher=suggested) (help); Unknown parameter|Title=ignored (|title=suggested) (help); Unknown parameter|Year=ignored (|year=suggested) (help) Not easy to read, but one of the few textbooks to offer an introduction to the important Newman/Penrose formalism. Also features much material on gravitational waves.
- . ISBN 0-521-42908-0.
{{cite book}}: Missing or empty|title=(help); Unknown parameter|Author=ignored (|author=suggested) (help); Unknown parameter|Publisher=ignored (|publisher=suggested) (help); Unknown parameter|Title=ignored (|title=suggested) (help); Unknown parameter|Year=ignored (|year=suggested) (help) This book is billed as an introductory textbook, but has no exercises and may be hard to read. Unique features include a chapter on measurement theory for general relativity, plus an introduction to tetrad formalism.
Online notes and courses
- Baez, Bunn, 2001, The Meaning of Einstein's Equation, intuitive explanation of Einstein-Hilbert equations - requires familiarity with special relativity.
- Carroll, Sean M., A No-Nonsense Introduction to General Relativity. Also see the notes from an earlier version of his above textbook: arXiv:gr-qc/9712019.
- MIT 8.962 Course Notes Notes and handouts from the MIT 8.962 course on General Relativity
- MIT OCW Site Notes and resources from the MIT open Courseware website
- Reflections on Relativity A complete online course on Relativity
Other
- Bondi, Herman, Relativity and Common Sense, Heinemann (1964). A school level introduction to the principle of relativity by a renowned scientist.
- Einstein, Albert, Relativity: The special and general theory. ISBN 0517884410. The special and general relativity theories in their original form.
- Epstein, Lewis Caroll, Relativity Visualized. ISBN 093521805X. Requires no mathematical background. Actually explains general relativity, rather than merely hinting at it with a few metaphors.
- Perret, W. and G.B. Jeffrey, trans.: The Principle of Relativity: A Collection of Original Memoirs on the Special and General Theory of Relativity, New York Dover (1923).
- Thorne, Kip, and Stephen Hawking, Black Holes and Time Warps, Papermac (1995). A recent popular account by leading experts.
- J. J. O'Connor and E. F. Robertson, History of General Relativity at the MacTutor History of Mathematics archive.
- The original 1915 article by David Hilbert containing the gravitational field equation.
- Malcolm MacCallum's GR News service for current research in relativity.
- Thomas A. Ryckman's Early Philosophical Interpretations of GR Stanford Encyclopedia of Philosophy
| Major branches of physics | |
|---|---|
| Divisions | |
| Approaches | |
| Classical | |
| Modern | |
| Interdisciplinary | |
| Related | |
]
Categories: matrix (i.e., just a number) called the Gaussian or
matrix (i.e., just a number) called the Gaussian or  .
.
 .
.
 .
.