| Revision as of 16:25, 22 April 2012 editBrews ohare (talk | contribs)47,831 edits →Comments: Just plain Bill; Srleffler← Previous edit | Revision as of 17:29, 22 April 2012 edit undoJust plain Bill (talk | contribs)Extended confirmed users, Pending changes reviewers25,210 edits →Comments: commentNext edit → | ||
| Line 200: | Line 200: | ||
| :::::''Hi Srleffler'': I am happy that you see wavelength plays a role in Fourier series for spatially periodic functions. Your general approach to rejection of this observation in ] is that somehow the importance of wavelength to Fourier series does not support its mention here because Fourier series is "not relevant to wavelength". That stance seems strange to me. You point out that this type of objection is not universally applicable, so for instance a ''pumpkin'' might be referred to in an article on ''vegetables'', and ''vice versa''. Perhaps you could explain further why the connection of wavelength to the sub-domain of Fourier series for spatially varying functions is of no interest to those interested in wavelength? Aren't readers of ] entitled to know about this connection to a truly gigantic area of mathematics? ] (]) 16:25, 22 April 2012 (UTC) | :::::''Hi Srleffler'': I am happy that you see wavelength plays a role in Fourier series for spatially periodic functions. Your general approach to rejection of this observation in ] is that somehow the importance of wavelength to Fourier series does not support its mention here because Fourier series is "not relevant to wavelength". That stance seems strange to me. You point out that this type of objection is not universally applicable, so for instance a ''pumpkin'' might be referred to in an article on ''vegetables'', and ''vice versa''. Perhaps you could explain further why the connection of wavelength to the sub-domain of Fourier series for spatially varying functions is of no interest to those interested in wavelength? Aren't readers of ] entitled to know about this connection to a truly gigantic area of mathematics? ] (]) 16:25, 22 April 2012 (UTC) | ||
| :::::''Just plain Bill'': The suggested text is not " backing Fourier series into a discussion of wavelength". The idea of wavelength is introduced in the article via the periodicity condition ''f''(''x−vt+λ'')=''f''(''x−vt''). That is exactly and inescapably the subject of Fourier series. Pointing out that connection in a sourced sentence is hardly a large cost to this article in terms of added space. ] (]) 16:25, 22 April 2012 (UTC) | :::::''Just plain Bill'': The suggested text is not " backing Fourier series into a discussion of wavelength". The idea of wavelength is introduced in the article via the periodicity condition ''f''(''x−vt+λ'')=''f''(''x−vt''). That is exactly and inescapably the subject of Fourier series. Pointing out that connection in a sourced sentence is hardly a large cost to this article in terms of added space. ] (]) 16:25, 22 April 2012 (UTC) | ||
| {{od|5}}The suggested text has been through at least three iterations since that green box appeared above. To a reader passing by, it is no longer apparent which version was being discussed at various times. I would prefer to see new suggestions given their own space where they were introduced, without obliterating the previous one(s). | |||
| Wavelength may be helpful in understanding some applications of Fourier series. Fourier analysis is not necessarily helpful in understanding wavelength. That's the asymmetry I meant by "backing into." Space on the page is one thing, but introducing tangential material is, IMO, a distraction to the reader. Sourced, you say... it is our job to be selective about which sources are relevant to the subject. __ ] (]) 17:29, 22 April 2012 (UTC) | |||
Revision as of 17:29, 22 April 2012
| Physics B‑class High‑importance | ||||||||||
| ||||||||||
|
Archives |
Question
What is the wavelength of this wave?  What is the exact definion of wavelength? By Fourier Analysis? ––虞海 (Yú Hǎi) 17:37, 10 October 2010 (UTC)
What is the exact definion of wavelength? By Fourier Analysis? ––虞海 (Yú Hǎi) 17:37, 10 October 2010 (UTC)
- Is that a meaningful question? What do the authorities define as "wavelength" ? --Wtshymanski (talk) 17:56, 10 October 2010 (UTC)
- Please, per wp:talk page guidelines, take this to the wp:reference desk/science? Thanks. DVdm (talk) 18:09, 10 October 2010 (UTC)
- It doesn't sound like a ref desk question to me, but rather a rhetorical question to see whether we have included a correct and working definition. I don't know of a definition based on Fourier analysis, but there are many alternatives, and maybe one of those, too. Some definitions are predicated on the wave being periodic; others on it being sinusoidal. The "distance between peaks or troughs" definition is usually adequate, and would give a sensible answer for the wave in question, but it may not be both precise and general enough to cover all things that people call wavelength. Dicklyon (talk) 19:57, 10 October 2010 (UTC)
- For slowly-varying and coherent wave trains a good definition is the one by Whitham (see e.g. his book Linear and nonlinear waves) through the definition of the wavenumber as the gradient of the carrier-wave phase θ(x,t): k=∇θ, so λ=2π/|k|. The wave phase of the carrier wave is obtainable through the Hilbert transform of the band-pass filtered signal (removing nonlinear sub- and super-harmonics). -- Crowsnest (talk) 22:05, 10 October 2010 (UTC)
- It's not even clear that this is a meaningful question. Not all waveforms have "a wavelength". General waveforms are composed of a spectrum of waves at different frequencies. One can only define an overall wavelength for a waveform in special cases.
- Be sure to read Archive 2 of this talk page (link above). This kind of question has been discussed here before.--Srleffler (talk) 23:09, 10 October 2010 (UTC)
- Ha! That's not likely to be a productive use of time. I like the definition that Crowsnest came up with, though. It works well for any wave that's remotely like sinusoidal. Dicklyon (talk) 23:16, 10 October 2010 (UTC)
Prism and refraction
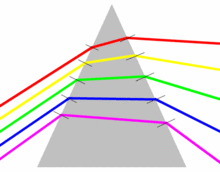
this edit removed the figure at the right with the explanation:
- "Rm disputed image altogether. It is not really relevant to the topic here. We are more interested in change in velocity as a function of frequency than in change of direction."
The figure was part of the section discussing dispersion:
- the relationship between ω and λ (or k) is called a dispersion relation.

So the topic is the change in the relation between ω and λ introduced by the refractive index of a medium, as indicated in the lower figure. The connection to the prism is via the Fresnel equations which explain that the angle of refraction varies with the refractive index, and thus, when n = n(λ), different colors are refracted by different angles according to Snell's law:
The inclusion of this point is of interest because the separation of colors using a prism is a well-known phenomenon, and its introduction here provides a useful connection for the reader to these topics. It is one of WP's most admired features that it serves to broaden the reader's concept of a topic by pointing out exactly such connections.
On this basis, I'd suggest the reintroduction of this figure with a better explanation and some links to the relevant WP articles on the related topics. Brews ohare (talk) 13:47, 2 April 2012 (UTC)
I have made an attempt at incorporating this suggestion. Brews ohare (talk) 18:32, 2 April 2012 (UTC)
- If we are going to include an image of a prism dispersing light, it should be the one showing moving waves, because the topic of this article is wavelength, and the relevant effect is that dispersion causes waves with different wavelengths to move with different velocities in the medium. It is interesting that this is related to the angle of refraction, but the latter is not directly relevant to the topic of this article. --Srleffler (talk) 03:53, 3 April 2012 (UTC)
- I removed the details about Snell's law and re-introduced links to the article on dispersion. The fact that prism dispersion is connected with change in wavelength in a medium is interesting and relevant. The details of how to calculate angle of dispersion in a prism are not relevant, and should be found in the linked articles if a reader is interested.
- I restored the image that actually shows waves moving with different speeds in a prism, connected with dispersion of light in that prism, because that is the relevant phenomenon here.--Srleffler (talk) 04:54, 3 April 2012 (UTC)
- I moved the discussion of refraction from an earlier section down to this one and modified the text a bit to fit it in more smoothly. Brews ohare (talk) 13:43, 3 April 2012 (UTC)
phase and group velocity

This topic may seem to be a digression in the article on wavelength. I am unsure how to handle it, but it shouldn't be ignored altogether. One aspect is shown in the figure: the wavelength of an envelope function differs from that of the constituents and moves at a different speed. Brews ohare (talk) 15:14, 3 April 2012 (UTC)
- DickLyon: This material is not "off-topic bloat". It is relevant for several reasons. Perhaps the main reason is that it points out the wavelength of a combination waveform is not that of its constituents. Another reason is that the this section concerns effects of the dependence of speed of propagation upon wavelength, and this phenomena is one of those consequences. Brews ohare (talk) 18:02, 3 April 2012 (UTC)
As we discussed at length, years ago, the application of the term "wavelength" to the modulation is rare and unusual, dare I say idiosyncratic. And there are much better places to discuss phase velocity and group velocity than an article on wavelength, which already goes off on too many tangents. Dicklyon (talk) 20:04, 3 April 2012 (UTC)
- Indeed "wavelength" is hardly ever used for this: I know it under the names group length, modulation length or envelope length. -- Crowsnest (talk) 20:53, 3 April 2012 (UTC)
- Crowsnest: Thanks for those links that establish some terminology I was unaware of. It does seem, however, that if one has an envelope f that satisfies the normal definition of a periodic function, that is,
- with ξ = x-vt there is no doubt whatsoever that the normal definition of wavelength applies to this envelope function f, whatever name one may attach to the envelope itself. Don't you agree? Brews ohare (talk) 21:39, 3 April 2012 (UTC)
- Crowsnest: Thanks for those links that establish some terminology I was unaware of. It does seem, however, that if one has an envelope f that satisfies the normal definition of a periodic function, that is,
- It's logical that the term could apply, but it's seldom or never used that way, so let's not. Dicklyon (talk) 00:27, 4 April 2012 (UTC)
- The terms "group length", modulation length" and "envelope length" definitely are used to apply to the length of a wave packet, but I haven't found them used for a periodic envelope like that in the image above. In any event, it is not only "logical" to use the term wavelength in connection with a periodic envelope function, it is mathematically perfectly and completely correct according to the definition of a periodic function. Brews ohare (talk) 01:28, 4 April 2012 (UTC)
- Misplaced Pages relies on sources, not logic. Our role is to report what is documented in reliable sources, not to synthesize our own knowledge, even when that knowledge follows logically from the source materials. See Misplaced Pages:No original research and WP:SYNTHESIS for more on this.--Srleffler (talk) 03:10, 4 April 2012 (UTC)
- That is of course absurd; if we didn't use logic, we'd be forced to make word for word copies of sources. --Wtshymanski (talk) 03:35, 4 April 2012 (UTC)
- Brews is arguing that we should cover a usage of a term purely because it is a logical extension of the usual definition, despite admitting that he hasn't found any sources that use the term that way. This is pretty clearly not allowed by policy.--Srleffler (talk) 04:37, 4 April 2012 (UTC)
- That is of course absurd; if we didn't use logic, we'd be forced to make word for word copies of sources. --Wtshymanski (talk) 03:35, 4 April 2012 (UTC)
- Misplaced Pages relies on sources, not logic. Our role is to report what is documented in reliable sources, not to synthesize our own knowledge, even when that knowledge follows logically from the source materials. See Misplaced Pages:No original research and WP:SYNTHESIS for more on this.--Srleffler (talk) 03:10, 4 April 2012 (UTC)
- The terms "group length", modulation length" and "envelope length" definitely are used to apply to the length of a wave packet, but I haven't found them used for a periodic envelope like that in the image above. In any event, it is not only "logical" to use the term wavelength in connection with a periodic envelope function, it is mathematically perfectly and completely correct according to the definition of a periodic function. Brews ohare (talk) 01:28, 4 April 2012 (UTC)
- It's logical that the term could apply, but it's seldom or never used that way, so let's not. Dicklyon (talk) 00:27, 4 April 2012 (UTC)
There is no "logical extension" of the definition of wavelength involved here. If a function f satisfies
then λ is its wavelength. Period. The only point to discuss is whether periodic envelopes are worth mentioning. I'd guess that DickLyon and Srleffler would say "No, it is an uninteresting topic". Dismissing the matter on spurious grounds simply avoids the real basis for discussion. Brews ohare (talk) 05:46, 4 April 2012 (UTC)
Some references are: Stade and Holbrow et al. Brews ohare (talk) 15:07, 4 April 2012 (UTC)
- Your first ref is not about waves, and the second is about sinusoidal waves; so what's your point? Dicklyon (talk) 15:33, 4 April 2012 (UTC)
- Shouldn't all the discussion about propagation, dispersion, and other properties of waves be left to the article Wave? That would turn this article into a dictdef that could be moved to Wiktionary. --Wtshymanski (talk) 14:46, 4 April 2012 (UTC)
- Wavelength is a property of waves, and it is sufficiently complicated to require its own article rather than loading down Wave. Brews ohare (talk) 15:07, 4 April 2012 (UTC)
- We need the right compromise. There's a lot to say about wavelength, and we've pretty much said that and more. Other stuff is better off in an article on waves. Dicklyon (talk) 15:33, 4 April 2012 (UTC)
- Dick: You have returned the discussion to the proper subject: is the treatment of periodic envelope functions "other stuff", or something that should be in the article? There is already a section Envelope_waves; perhaps this material should go there? Brews ohare (talk) 16:45, 4 April 2012 (UTC)
- As you recall, we had a big to-do about that back in June/July 2009, before your year of topic-ban from physics and your year of block for continuing disruptions. I condensed what you had about envelopes and found the one source that connected that to "wavelength". If there are more sources that connect envelope waves to the concept of wavelength, bring those forward for consideration. Dicklyon (talk) 17:02, 4 April 2012 (UTC)
- Dick: You have returned the discussion to the proper subject: is the treatment of periodic envelope functions "other stuff", or something that should be in the article? There is already a section Envelope_waves; perhaps this material should go there? Brews ohare (talk) 16:45, 4 April 2012 (UTC)
- We need the right compromise. There's a lot to say about wavelength, and we've pretty much said that and more. Other stuff is better off in an article on waves. Dicklyon (talk) 15:33, 4 April 2012 (UTC)
- Wavelength is a property of waves, and it is sufficiently complicated to require its own article rather than loading down Wave. Brews ohare (talk) 15:07, 4 April 2012 (UTC)
Dick: You digress. Past squabbles I suppose are meant to underline how difficult we are. Instead, we might focus upon the present: periodic envelope functions exist. They therefore have a wavelength. Is this a topic suitable for the section Envelope_waves? I don't think the question is one of "Do periodic envelopes exist?" nor "Do periodic envelopes have a wavelength?" Maybe the question is "Is it of interest that a composite of short-wavelength, fast-moving excitations can form a disturbance in a dispersive medium that has a longer wavelength and moves at a different speed?" Brews ohare (talk) 17:24, 4 April 2012 (UTC)
- Brews, above you write "If a function f satisfies then λ is its wavelength. Period." I disagree. Waves have wavelength, functions do not. A periodic envelope is not a wave, although a wave can have a periodic envelope. The wavelength of a wave with a periodic envelope is not the spatial period of the envelope function.--Srleffler (talk) 02:27, 5 April 2012 (UTC)
- Srleffler, if I understand you, you would accept instead a statement: "If a function f satisfies f(ξ+λ) = f(ξ) and this function describes a waveform with a wavelength λ, then in the math describing this wave, the physical wavelength corresponds to the period of the describing periodic function." So the distinction here is one of semantics: whether a term described in physics as a "wavelength" has a mathematical analogue that might be called the wavelength of a function, or might be called something else. I have a feeling of vertigo here, of falling into some kind of debate over whether nature is imperfect and math is the more prefect Platonic reality.
- Your second point is that the wavelength of a wave with an envelope is not the spatial period of the envelope. I suspect this is an exercise in semantics also. I suppose you might agree that the envelope is a physical item, and that an envelope can have a wavelength. That wavelength is not, of course, the wavelength of the component waves, if that is your object here. However, if the envelope is described by a periodic function, then the spatial period of that function represents the wavelength of the envelope in the mathematics. Brews ohare (talk) 05:12, 5 April 2012 (UTC)
- Not clear what semantics you intend by "is a physical item", but it's very unusual to speak of the envelope as a wave or having a wavelength. I've found exactly one source that does so, and cited it (Denny). And what it says about the envelope's velocity being determined by its wavelength is wrong, or at least seriously misleading, though the rest of its derivation of group velocity is pretty conventional. If that's all we've got, I don't see a need to extrapolate the concept of wavelength to envelope functions. Nobody does that. Dicklyon (talk) 06:27, 5 April 2012 (UTC)

- The most common use of the term "envelope" is to describe a wave packet, which of course has no wavelength, being a solitary propagating pulse. However, as shown in the image, envelopes can have a wavelength. Moreover, this particular example provides a vivid illustration of the fact that the envelope propagates at a different speed than its constituents. The group velocity is pointed out already in the section on Envelope_waves, and an illustration is worth 1000 words. It seems to me that "it is of interest that a composite of short-wavelength, fast-moving excitations can form a periodic disturbance in a dispersive medium that has a longer wavelength and moves at a different speed than its constituent waves." Don't you think some presentation of this matter could be constructed that would be acceptable to you? Brews ohare (talk) 15:09, 5 April 2012 (UTC)
- Who are you quoting here? And why is this more interesting than the case of two irrationally related sinusoids forming a non-periodic disturbance? And anyway, the periodic disturbance doesn't propagate unchanged in a dispersive medium as your illustration shows; the envelope does, but that's not a disturbance. Dicklyon (talk) 15:25, 5 April 2012 (UTC)
- Dick: The subject of this article is wavelength. So an example of a periodic envelope that exhibits a wavelength is ipso facto more pertinent to this topic than a non-periodic disturbance. And a picture comparing group and phase velocity is more illuminating than a bare mention in words: "a composite of short-wavelength, fast-moving excitations can form a periodic disturbance in a dispersive medium that has a longer wavelength and moves at a different speed than its constituent waves"; although that sentence would be helpful too. Brews ohare (talk) 15:46, 5 April 2012 (UTC)
- As you are more application oriented, maybe Figure 7.1 here is of interest? It is not an example of dispersive media, but it is an example of an envelope that has a wavelength. Brews ohare (talk) 16:06, 5 April 2012 (UTC) Another possible example which involves a dispersive and nonlinear medium is a train of solitons and here. In the ocean the lowest graph here may be of interest. I don't think these examples are for the article, just for illustration here. Brews ohare (talk) 16:23, 5 April 2012 (UTC)
- I discovered that the reference you found for the envelope discussion also uses the term wavelength for the envelope, so I made that observation in the envelope section. Brews ohare (talk) 18:43, 5 April 2012 (UTC)
- As I said, that Denny ref is the only source I can find that associates the concept of "wavelength" with the envelope length. And some of what it says about it is wrong or misleading. None of your other links go to pages with "wavelength" anywhere nearby. So I think that even mentioning this concept is UNDUE weight. Dicklyon (talk) 19:21, 5 April 2012 (UTC)
- The misleading bit is "the envelope of modulation...moves at a speed that is determined by its own wavelength and period", which is either trivial or wrong. The speed is determined by the group velocity, or d\omega/dk, in the region of the two wavelengths, and is pretty much independent of the "wavelength" of the modulation envelope. This is a very poor explanation all around, and not one the gives any weight to the idea that an envelope modulation is referred to as having a wavelength different from the mean wavelength of the underlying waves (as is done in talking about modulated radio and light waves, for example). Dicklyon (talk) 19:33, 5 April 2012 (UTC)
- Who are you quoting here? And why is this more interesting than the case of two irrationally related sinusoids forming a non-periodic disturbance? And anyway, the periodic disturbance doesn't propagate unchanged in a dispersive medium as your illustration shows; the envelope does, but that's not a disturbance. Dicklyon (talk) 15:25, 5 April 2012 (UTC)
- The most common use of the term "envelope" is to describe a wave packet, which of course has no wavelength, being a solitary propagating pulse. However, as shown in the image, envelopes can have a wavelength. Moreover, this particular example provides a vivid illustration of the fact that the envelope propagates at a different speed than its constituents. The group velocity is pointed out already in the section on Envelope_waves, and an illustration is worth 1000 words. It seems to me that "it is of interest that a composite of short-wavelength, fast-moving excitations can form a periodic disturbance in a dispersive medium that has a longer wavelength and moves at a different speed than its constituent waves." Don't you think some presentation of this matter could be constructed that would be acceptable to you? Brews ohare (talk) 15:09, 5 April 2012 (UTC)
I'll take a look for a better source. I was interested in pointing out wavelength of envelope as simply an example of the concept of wavelength, and not so much as a practical matter. I think that is a useful thing to do in driving home a concept. However, I have recently discovered there may be a very real application in what is called electric distance meters or EDMs, where a modulated light beam is used to measure distances in terms of the modulation length. An example discussion is here. What do you think about this? Brews ohare (talk) 19:38, 5 April 2012 (UTC)
- I have replaced Denny. It would seem that there are many possible replacements. Brews ohare (talk) 21:40, 5 April 2012 (UTC)
- I reverted you, because I do not see where the new reference applies the term 'wavelength' to the envelope. Did I miss it? A reference that uses the term "wavelength" in describing the envelope is crucial for including discussion of envelopes at all. Envelopes are barely worth mentioning at all in this article, and only because a tiny minority of authors describe the period of a periodic envelope as a "wavelength". --Srleffler (talk) 03:34, 6 April 2012 (UTC)
- Srleffler: The reference uses the term wave number, I believe, related as everyone knows to the reciprocal of wavelength, and as pointed out in the reverted text. I changed the reference because Dick pointed out some infelicities in Denny's discussion of group velocity. However, if you prefer to leave Denny instead of accepting a more suitable source or looking for one yourself, well that makes clear your priorities, I guess. Brews ohare (talk) 05:24, 6 April 2012 (UTC)
- Here is another possibility and here is a google book search for wavelength of a modulation envelope and here is one for modulation wavelength and here is one for envelope wavelength. Brews ohare (talk) 13:05, 6 April 2012 (UTC)
- I reverted you, because I do not see where the new reference applies the term 'wavelength' to the envelope. Did I miss it? A reference that uses the term "wavelength" in describing the envelope is crucial for including discussion of envelopes at all. Envelopes are barely worth mentioning at all in this article, and only because a tiny minority of authors describe the period of a periodic envelope as a "wavelength". --Srleffler (talk) 03:34, 6 April 2012 (UTC)
Mathematical representation
The article in its present form describes wavelength using a sine wave image and generalizes this simple case with the remark:
- The concept can also be applied to periodic waves of non-sinusoidal shape
A more fundamental and rigorous approach would be to point out that a Fourier series assembled from sinusoidal functions of the form:
(n a positive integer) in the form:
represents any (bounded and integrable) function in the interval −λ/2 ≤ ξ < λ/2. This function has the property that it repeats periodically in ξ as described by:
where λ is variously called the period or the wavelength of the function. By choosing
where x is distance along an axis in space and t is time, the function f describes a waveform periodic in space with wavelength λ propagating with time-invariant shape in the positive x direction with a velocity v.
References
- Eric Stade (2011). Fourier Analysis. John Wiley & Sons. p. 3. ISBN 1118165519.
- Gerald B Folland (2009). "Chapter 2: Fourier Series". Fourier Analysis and Its Applications. American Mathematical Society. pp. 18 ff. ISBN 0821847902.
- Llewelyn Southworth Lloyd (1937). Music and sound. Ayer Publishing. p. 156. ISBN 0836951883.
- Eugene Hecht (1975). Schaum's outline of theory and problems of optics. McGraw-Hill Professional. p. 205. ISBN 0070277303.
- Andrew Putnis (1992). An Introduction to Mineral Sciences. Cambridge University Press. p. 65. ISBN 0521429471.
Fourier analysis is a mathematical method of expressing any periodic function with wavelength λ as a sum of sinusoidal functions whose wavelengths are integral fractions of λ (i.e. λ, λ/2, λ/3, etc.)
I don't think this description need appear in the introduction, but perhaps in the section Mathematical representation. It should appear in Wavelength because it is a general concept of wavelength for waves of arbitrary shape, and makes the connection to Fourier series, which is an important idea in the theory of waves that the reader should become aware of. Brews ohare (talk) 16:28, 4 April 2012 (UTC)
- The first hardly mentions waves, and in the one example where it does, it has the wavelength in milliseconds – hardly a useful source for wavelength. The second doesn't appear to mention wavelength at all. Let's not make this an article on Fourier series or periodic functions. Dicklyon (talk) 17:09, 4 April 2012 (UTC)
- Apparently the mention of Fourier series makes this about Fourier series. That is like saying the mention of Hilbert space makes an article on quantum mechanics about Hilbert space. I think you can address this suggestion more seriously. Brews ohare (talk) 17:28, 4 April 2012 (UTC)
- Although it is difficult to take seriously your suggestion that Fourier series are unrelated to wavelength, I've added
twothree more sources that make this point verbatim. Brews ohare (talk) 17:50, 4 April 2012 (UTC)
- Brews, I don't see any benefit at all in introducing the treatment you describe to this article. It adds a bunch of math that conveys no relevant information that is not already covered in the article.--Srleffler (talk) 02:34, 5 April 2012 (UTC)
- Agreed. Any complete transform, orthogonal or otherwise, would give the same result, which is that a periodic function can be decomposed as a sum. I can't see what introducing Fourier transforms or series here does for the concept of wavelength, or why this transform is more interesting than, say, a Haar transform, or polynomials, or sinc functions, or wavelets. It's not clear why Brews call this "A more fundamental and rigorous approach". Of course, I understand that sinusoids, being the eigenfunctions of continuous-time linear systems, do have a special role to play, especially in analyzing dispersion, or how the shape of a wave changes with location. That, however, it a topic incompatible with this assumption of periodic functions what propagate while holding their shape. The sinusoidal decomposition would be useful in an article on wave propagation and dispersion, but I can't see how it's helpful here. Dicklyon (talk) 04:24, 5 April 2012 (UTC)
- Dicklyon and Srleffler: I believe you both misunderstand the purpose of mentioning Fourier series here. It introduces the mathematical background for expressing a general periodic waveform as a superposition of simple sinusoids. It is the mathematical extension of the remark in the introduction that "The concept can also be applied to periodic waves of non-sinusoidal shape". It is most simply applicable in non-dispersive media, as the Fourier series in its simplest form describes propagation of a wave of fixed shape .
- It seems to me that these simple remarks can assist readers to understand the use of Fourier series in the general application of the concept of wavelength, and lead them to the relevant WP articles on this topic. Such connections are a major part of the value of WP, as is attested to in almost every appraisal.
- Your remarks indicate a bias against mathematical explanation. That is your personal right, of course, but it should not be imposed upon every reader of WP.
- So I suggest that you provide some sensible objections to this well-sourced and pertinent addition to the article.Brews ohare (talk) 15:00, 5 April 2012 (UTC)
- I think you're still very confused about the physical/mathematical purpose of decomposing a periodic wave into sinusoidal components. Nothing in what you've said takes any advantage of the components being sinusoidal, and in a nondispersive medium, there is no advantage that I'm aware of, since all the components have the same velocity and you might as well just propagate the original waveform. I have no bias against using a decomposition into eigenfunctions to help analyze a linear system, but that's not what you're doing. Dicklyon (talk) 15:22, 5 April 2012 (UTC)
- OK, Dick. I see that you have a completely different orientation to this topic than I intend. Maybe I can explain better. The subject of this article is wavelength, and I wish to stick very closely to that topic. The introduction says, as mentioned above, "The concept can also be applied to periodic waves of non-sinusoidal shape". I pose this question: how would you support this statement mathematically? Suppose for the moment that you want to undertake that support. The most general "periodic wave of non-sinusoidal shape" is a Fourier series. As stated by Andrew Putnis (1992). An Introduction to Mineral Sciences. Cambridge University Press. p. 65. ISBN 0521429471.
Fourier analysis is a mathematical method of expressing any periodic function with wavelength λ as a sum of sinusoidal functions whose wavelengths are integral fractions of λ (i.e. λ, λ/2, λ/3, etc.)
. That is the point I want to drive home to the reader. Brews ohare (talk) 15:30, 5 April 2012 (UTC)- Even if it were useful to support the statement mathematically, it is not clear to me that you have done so. As I see it, the application of "wavelength" to the spatial period of a non-sinusoidal wave is purely a matter of definition. It doesn't really matter whether one says that the distance over which the wave repeats is its "wavelength", or that the "wavelength" of the wave is equal to the wavelength of the lowest-order component in its Fourier series. These are the same thing; neither is more fundamental than the other. The only difference between them is that the Fourier-based explanation is harder to understand. Fourier expansions can be very useful, and are often helpful in understanding the fundamental physics of a system. In this case, however, the expansion is not useful, and does not make the physics any clearer.--Srleffler (talk) 03:12, 6 April 2012 (UTC)
- Srleffler: It is now apparent that you do not understand the relation between math and the physics it describes. Brews ohare (talk) 05:37, 6 April 2012 (UTC)
- And it's not clear what point you're trying to drive home to the reader, or how a sinusoidal decomposition helps. Your statement that "The most general 'periodic wave of non-sinusoidal shape' is a Fourier series" is complete hogwash; it's no more general than any other description of a periodic wave, which was my point in mention some of the other possible decompositions. If there's something special about sinusoids, you need to understand what that is. Fourier used them because they were the eigensolutions of the system he was analyzing, and that's the kind of physical situation where they become helpful. They are very helpful indeed for analyzing waves in continuous linear systems that are dispersive, but mentioning them as you did there gives no connection to that. And you can't even start to do a Fourier series of a periodic wave until after you've identified the period, so it seems all the more pointless. As for the application of the concept of wavelength to waves of nonsinusoidal shape, even that is a rather minority usage; usually it's applied only to waves that are at least locally nearly sinusoidal, or have one crest and one trough per cycle, so there's an obvious meaning to distance between adjacent crests or troughs. The extension to arbitrary periodic waves doesn't include the usual not-quite periodic case, but opens up a can of worms in terms of different periods (and near periods), in way that is very seldom encountered in the literature; just ref 18. Dicklyon (talk) 04:43, 6 April 2012 (UTC)
- Your view that it is "hogwash" to say a Fourier series can represent the most general (bounded, integrable) periodic function means to me that either (i) you misread the statement as some kind of claim that only a Fourier series can do this, which was never said, or (ii) you have no idea what is going on. I'll adopt the first view, just for the sake of things. The rest of your discussion about why exactly Fourier did what he did and where eigenfunctions are helpful is not part of the discussion. Dick, you are so anxious to argue applications that you cannot get the subject of the discussion straight. The object is to provide mathematical support to the statement ""The concept can also be applied to periodic waves of non-sinusoidal shape". There is nothing in this statement of simple fact or its mathematical support that relates to your comments. Brews ohare (talk) 05:37, 6 April 2012 (UTC)
- The statement I objected to was ""The most general 'periodic wave of non-sinusoidal shape' is a Fourier series", not "a Fourier series can represent the most general (bounded, integrable) periodic function". And as Srleffler pointed out, this mathematical complication is in no way providing support for the statement that "The concept can also be applied to periodic waves of non-sinusoidal shape". I admit to being completely baffled by what your point is in introducing sinusoidal decomposition of periodic functions here. Dicklyon (talk) 06:04, 6 April 2012 (UTC)
- Your view that it is "hogwash" to say a Fourier series can represent the most general (bounded, integrable) periodic function means to me that either (i) you misread the statement as some kind of claim that only a Fourier series can do this, which was never said, or (ii) you have no idea what is going on. I'll adopt the first view, just for the sake of things. The rest of your discussion about why exactly Fourier did what he did and where eigenfunctions are helpful is not part of the discussion. Dick, you are so anxious to argue applications that you cannot get the subject of the discussion straight. The object is to provide mathematical support to the statement ""The concept can also be applied to periodic waves of non-sinusoidal shape". There is nothing in this statement of simple fact or its mathematical support that relates to your comments. Brews ohare (talk) 05:37, 6 April 2012 (UTC)
- Even if it were useful to support the statement mathematically, it is not clear to me that you have done so. As I see it, the application of "wavelength" to the spatial period of a non-sinusoidal wave is purely a matter of definition. It doesn't really matter whether one says that the distance over which the wave repeats is its "wavelength", or that the "wavelength" of the wave is equal to the wavelength of the lowest-order component in its Fourier series. These are the same thing; neither is more fundamental than the other. The only difference between them is that the Fourier-based explanation is harder to understand. Fourier expansions can be very useful, and are often helpful in understanding the fundamental physics of a system. In this case, however, the expansion is not useful, and does not make the physics any clearer.--Srleffler (talk) 03:12, 6 April 2012 (UTC)
- OK, Dick. I see that you have a completely different orientation to this topic than I intend. Maybe I can explain better. The subject of this article is wavelength, and I wish to stick very closely to that topic. The introduction says, as mentioned above, "The concept can also be applied to periodic waves of non-sinusoidal shape". I pose this question: how would you support this statement mathematically? Suppose for the moment that you want to undertake that support. The most general "periodic wave of non-sinusoidal shape" is a Fourier series. As stated by Andrew Putnis (1992). An Introduction to Mineral Sciences. Cambridge University Press. p. 65. ISBN 0521429471.
- I think you're still very confused about the physical/mathematical purpose of decomposing a periodic wave into sinusoidal components. Nothing in what you've said takes any advantage of the components being sinusoidal, and in a nondispersive medium, there is no advantage that I'm aware of, since all the components have the same velocity and you might as well just propagate the original waveform. I have no bias against using a decomposition into eigenfunctions to help analyze a linear system, but that's not what you're doing. Dicklyon (talk) 15:22, 5 April 2012 (UTC)
- Agreed. Any complete transform, orthogonal or otherwise, would give the same result, which is that a periodic function can be decomposed as a sum. I can't see what introducing Fourier transforms or series here does for the concept of wavelength, or why this transform is more interesting than, say, a Haar transform, or polynomials, or sinc functions, or wavelets. It's not clear why Brews call this "A more fundamental and rigorous approach". Of course, I understand that sinusoids, being the eigenfunctions of continuous-time linear systems, do have a special role to play, especially in analyzing dispersion, or how the shape of a wave changes with location. That, however, it a topic incompatible with this assumption of periodic functions what propagate while holding their shape. The sinusoidal decomposition would be useful in an article on wave propagation and dispersion, but I can't see how it's helpful here. Dicklyon (talk) 04:24, 5 April 2012 (UTC)
Dick: Your bafflement is due to your fixation on the wrong subject. The matter is logically as follows:
- The statement is made in the introduction that "The concept can also be applied to periodic waves of non-sinusoidal shape".
- The observation now can be made that any periodic wave can be represented by a Fourier series.
- The wavelength of a wave represented by a Fourier series is that of the leading sinusoidal term.
- QED
There is no need to inquire into the apparatus of generalized Fourier series, what to do with quasi-periodic functions, or any of the other issues you have brought up. Brews ohare (talk) 12:40, 6 April 2012 (UTC)
- This explanation of your idea avoids some of the difficulties encountered above. The problem with it is that nothing is proved; there is no "QED". Step 3 is simply a definition of the term "wavelength", as applied to nonsinusoidal waves. Defining the wavelength of such waves as the wavelength of the leading sinusoidal term is not better than defining it as the distance over which the function repeats in space; they are fundamentally the same thing. Your formalism doesn't provide any useful "mathematical support". It adds complexity, without being any more rigorous or any more useful.--Srleffler (talk) 04:44, 7 April 2012 (UTC)
- Srleffler: Of course they are the same thing; that is the whole point. That is the QED. The Fourier series shows a mathematical mechanism in principle for establishing the wavelength of an arbitrary periodic waveform. Brews ohare (talk) 15:43, 7 April 2012 (UTC)
- And it would be equally true and meaningless to use square waves, or triangle waves, or sawtooth waves. Of course, there are infinitely many periodic waveforms that would be missing a fundamental component (different ones for the different basis functions, though); so you could analyze it with different basis functions and hope to find at least one with a fundamental. To be sure to get one, you could use the function itself as the fundamental basis function. Gee, math is fun. Dicklyon (talk) 04:59, 7 April 2012 (UTC)
- Dick: of course Fourier series apply to square waves, or triangle waves, etc. That is what is meant by saying Fourier series applies to an arbitrary periodic function. And, again, there is no claim for uniqueness; we need only one way to establish the point, even though many ways may exist. Brews ohare (talk) 15:43, 7 April 2012 (UTC)
- Sorry if I was unclear. It's not that square waves can be decomposed into sinusoids. I'm saying you could equally well decompose your periodic function into square waves, or various other basis functions (even if they're not orthogonal, so not the usual generalization of Fourier transforms). In all such cases though, you need to know the period before you start, so how it has anything to do with "establishing the wavelength of an arbitrary periodic waveform" remains elusive. Dicklyon (talk) 15:49, 7 April 2012 (UTC)
- Dick: You are thinking in a practical manner again. The abstract notion here is to demonstrate that the thing can be done, not necessarily how to go about it. Brews ohare (talk) 15:54, 7 April 2012 (UTC)
- Actually, as Srleffler and the Fourier theorem itself state, as a practical matter, if one knows f(ξ+λ)=f(ξ) you already know the wavelength if you can establish λ as being the shortest such length; there may be anomalous cases where you aren't sure, and matching a Fourier representation to the function could help you decide what λ was. That seems most likely to arise when trying to approximate some experimental data with a background noise level. The technical point, however, is that the approach exists in principle, regardless of its practicality, and shows a λ can be found for an arbitrary periodic function. Brews ohare (talk) 16:18, 7 April 2012 (UTC)
- Sorry if I was unclear. It's not that square waves can be decomposed into sinusoids. I'm saying you could equally well decompose your periodic function into square waves, or various other basis functions (even if they're not orthogonal, so not the usual generalization of Fourier transforms). In all such cases though, you need to know the period before you start, so how it has anything to do with "establishing the wavelength of an arbitrary periodic waveform" remains elusive. Dicklyon (talk) 15:49, 7 April 2012 (UTC)
- Dick: of course Fourier series apply to square waves, or triangle waves, etc. That is what is meant by saying Fourier series applies to an arbitrary periodic function. And, again, there is no claim for uniqueness; we need only one way to establish the point, even though many ways may exist. Brews ohare (talk) 15:43, 7 April 2012 (UTC)
- And it would be equally true and meaningless to use square waves, or triangle waves, or sawtooth waves. Of course, there are infinitely many periodic waveforms that would be missing a fundamental component (different ones for the different basis functions, though); so you could analyze it with different basis functions and hope to find at least one with a fundamental. To be sure to get one, you could use the function itself as the fundamental basis function. Gee, math is fun. Dicklyon (talk) 04:59, 7 April 2012 (UTC)
- Srleffler: Of course they are the same thing; that is the whole point. That is the QED. The Fourier series shows a mathematical mechanism in principle for establishing the wavelength of an arbitrary periodic waveform. Brews ohare (talk) 15:43, 7 April 2012 (UTC)
Dick and Srleffler: Aside from providing a general technique to establish wavelength, there is value in pointing out the connection of wavelength to Fourier series for no other reason than Fourier series are a very fundamental part of functional analysis, and the connection of wavelength to this seminal apparatus has value for the reader all by itself. Brews ohare (talk) 15:54, 7 April 2012 (UTC)
Reference to Fourier series
|
Comment is sought as to whether a reference to Fourier series is appropriate under the heading general periodic waveforms. Some editors appear to find connecting Fourier series to wavelength is a digression. The text in question is provided below. Brews ohare (talk) 20:09, 20 April 2012 (UTC)
Text referring to Fourier series
This text is to appear following the equation defining the wavelength of a periodic function in the section More general waveforms, just before the header Envelope waves:
| The wavelength of a general periodic waveform is related mathematically to its Fourier series expression as a summation of sinusoidally varying waves: |
| .. "Fourier analysis is a mathematical method of expressing any periodic function with wavelength λ as a sum of sinusoidal functions whose wavelengths are integral fractions of λ (i.e. λ, λ/2, λ/3, etc.)" |
References
|
Author's remarks
- This text states the specific connection between wavelength and Fourier series as applied to spatial periodicity. It alerts readers to this connection between wavelength and some very important mathematics.
- Some discussion appears on this Talk page regarding a previous suggestion involving a more elaborate discussion of Fourier series presented here. That discussion is not pertinent in the present case because what we have here is a much more curtailed description. Brews ohare (talk) 13:47, 22 April 2012 (UTC)
Comments
"It is noteworthy that the wavelength of a general periodic waveform is related mathematically to its Fourier series expression..." is very odd. First of all, the source does not support a claim that "it is noteworthy"; that just sets off BS detectors. Second, the relationship of the wavelength (or the period) of a general periodic function to it Fourier series is simply that you need to know the former to compute the latter. How does this help explain or understand wavelength? And if he had used the word "period" like everyone else, would we even be discussing it? No. The only reason this guy cares about Fourier analysis of things with wavelengths is that he's doing X-Ray crystallography, and I don't think it's appropriate to get into that here; maybe a link from the crystals section would be OK. Dicklyon (talk) 01:57, 21 April 2012 (UTC)
- Dick, the source is cited as the origin of the quotation. I've moved the footnote to make this clearer.
- This author's use of "wavelength" in the quotation is entirely appropriate and accurate and often used. Ordinarily (although not invariably) period is taken to refer to periodicity in time or with respect to some general variable, say ξ or θ, while wavelength invariably refers to periodicity in space. Of course, periodicity can be expressed in many different ways, but wavelength is the subject here, and wavelength is used to define a periodic function in the subsection More general waveforms where this text referring to Fourier series is proposed to be placed. The mathematical definition is stated in the article as f(x−vt+λ)=f(x−vt). So I don't accept your stance that "wavelength" is being awkwardly squeezed into the discussion by using an uncommon usage of terminology.
- As for the importance of this topic, the entire subject of waveforms periodic in space with a certain wavelength is inextricably connected to Fourier series. Perhaps you can suggest some more innocuous wording to replace "noteworthy" that you would find acceptable? Brews ohare (talk) 15:25, 21 April 2012 (UTC)
- I'll wait until we get other comments. This is supposed to be a RFC, not us arguing some more. Dicklyon (talk) 15:46, 21 April 2012 (UTC)
- I removed "noteworthy" as unnecessary. Brews ohare (talk) 16:07, 21 April 2012 (UTC)
- I'll wait until we get other comments. This is supposed to be a RFC, not us arguing some more. Dicklyon (talk) 15:46, 21 April 2012 (UTC)
- I agree with Dicklyon. Fourier analysis is a tool for mathematical study of periodic functions. It has nothing in particular to do with wavelength. You can use Fourier analysis on a purely time-based phenomenon or an abstract function, neither of which has a wavelength. The Fourier series does not help readers understand waves or wavelength. Quite the opposite. And the source for the quote is a narrow technical one inappropriate for a mathematical article (and a commercial link is entirely inappropriate for a reference – let readers find that via the ISBN if they want to).--JohnBlackburnedeeds 19:56, 21 April 2012 (UTC)
- John, you are making a statement logically equivalent to this: A knife is a cutting implement so it is irrelevant to point out under "weapon" that a knife can be used this way. Likewise, Fourier analysis can be viewed as a general discussion of periodicity in any variable. So you claim in particular, and as is the topic here, it is irrelevant to point out its use to analyze spatial variation. Brews ohare (talk) 20:44, 21 April 2012 (UTC)
- You can reinterpret my statement as you like; my point is I agree with Dicklyon and now IRWolfie- that it doesn't belong.--JohnBlackburnedeeds 21:08, 21 April 2012 (UTC)
- John, no, the point is you "agree" with these editors but offer no reason for doing so, as I have pointed out. Brews ohare (talk) 00:57, 22 April 2012 (UTC)
- My reasons are here as you seem to have trouble finding them.--JohnBlackburnedeeds 11:04, 22 April 2012 (UTC)
- Right, John. As to your comments that you have linked with caustic observation about myself, I see again that you propose as a "reason" for your supposed "agreement" with DickLyon, that because Fourier series have wide application to periodicity in general, therefore my proposed text stating the specific connection between wavelength and Fourier series as applied to spatial periodicity is neither useful nor appropriate. I think you can see your position is neither logical nor sensitive to the key role of WP in broadening a reader's grasp of the context of a topic they are reading about. Brews ohare (talk) 13:39, 22 April 2012 (UTC)
- You can reinterpret my statement as you like; my point is I agree with Dicklyon and now IRWolfie- that it doesn't belong.--JohnBlackburnedeeds 21:08, 21 April 2012 (UTC)
- John, you are making a statement logically equivalent to this: A knife is a cutting implement so it is irrelevant to point out under "weapon" that a knife can be used this way. Likewise, Fourier analysis can be viewed as a general discussion of periodicity in any variable. So you claim in particular, and as is the topic here, it is irrelevant to point out its use to analyze spatial variation. Brews ohare (talk) 20:44, 21 April 2012 (UTC)
- Oppose It has nothing in particular to add to the topic of the article and thus strays off topic. IRWolfie- (talk) 20:24, 21 April 2012 (UTC)
- IRWolfie: How exactly is it straying off topic to point out the connection between wavelength and Fourier series for spatially periodic functions? Are you claiming the connection is not there, or that the role of wavelength does not enter the construction of a Fourier series for a spatially varying function? Either claim would directly contradict the cited sources (or in fact, any sources). Brews ohare (talk) 20:44, 21 April 2012 (UTC)
- The point is that wavelength is defined in general in terms of a general, spatially periodic waveform, and such waveforms are described by Fourier series having a particular relation to the wavelength of the waveform. That is a nontrivial observation and connects the topic of wavelength to the very important context of Fourier series. A sentence or two about this is not a serious expansion of the article and is a small addition to provide this important connection for the topic of wavelength. Brews ohare (talk) 01:35, 22 April 2012 (UTC)
- Regarding your first paragraph: the fact that wavelength plays a role in the construction of Fourier series does not help your argument. The problem is that the connection goes the wrong way. Wavelength is certainly relevant to Fourier series, but that does not imply that Fourier series are relevant to an article on wavelength. Relevance is not always bidirectional.
- Regarding the second paragraph: It is not clear to me that this observation is "nontrivial". --Srleffler (talk) 16:00, 22 April 2012 (UTC)
- I agree that backing Fourier series into a discussion of wavelength goes the wrong way around. A "See also" entry, or an inline wikilink such as the one in the section on wave packets, should suffice. __ Just plain Bill (talk) 16:17, 22 April 2012 (UTC)
- Hi Srleffler: I am happy that you see wavelength plays a role in Fourier series for spatially periodic functions. Your general approach to rejection of this observation in Wavelength is that somehow the importance of wavelength to Fourier series does not support its mention here because Fourier series is "not relevant to wavelength". That stance seems strange to me. You point out that this type of objection is not universally applicable, so for instance a pumpkin might be referred to in an article on vegetables, and vice versa. Perhaps you could explain further why the connection of wavelength to the sub-domain of Fourier series for spatially varying functions is of no interest to those interested in wavelength? Aren't readers of Wavelength entitled to know about this connection to a truly gigantic area of mathematics? Brews ohare (talk) 16:25, 22 April 2012 (UTC)
- Just plain Bill: The suggested text is not " backing Fourier series into a discussion of wavelength". The idea of wavelength is introduced in the article via the periodicity condition f(x−vt+λ)=f(x−vt). That is exactly and inescapably the subject of Fourier series. Pointing out that connection in a sourced sentence is hardly a large cost to this article in terms of added space. Brews ohare (talk) 16:25, 22 April 2012 (UTC)
- I agree that backing Fourier series into a discussion of wavelength goes the wrong way around. A "See also" entry, or an inline wikilink such as the one in the section on wave packets, should suffice. __ Just plain Bill (talk) 16:17, 22 April 2012 (UTC)
The suggested text has been through at least three iterations since that green box appeared above. To a reader passing by, it is no longer apparent which version was being discussed at various times. I would prefer to see new suggestions given their own space where they were introduced, without obliterating the previous one(s).
Wavelength may be helpful in understanding some applications of Fourier series. Fourier analysis is not necessarily helpful in understanding wavelength. That's the asymmetry I meant by "backing into." Space on the page is one thing, but introducing tangential material is, IMO, a distraction to the reader. Sourced, you say... it is our job to be selective about which sources are relevant to the subject. __ Just plain Bill (talk) 17:29, 22 April 2012 (UTC)
Categories:




