| Revision as of 23:44, 30 December 2012 editMeasureIT (talk | contribs)257 edits →Universal measure: expanded the discussion based on the sources← Previous edit | Revision as of 23:49, 30 December 2012 edit undoMeasureIT (talk | contribs)257 edits →Universal measure: from what I see in the sources citedNext edit → | ||
| Line 27: | Line 27: | ||
| |date = 15 July 2007 | |date = 15 July 2007 | ||
| |publisher = ] | |publisher = ] | ||
| |accessdate = 30 December 2012}}</ref> |
|accessdate = 30 December 2012}}</ref> Some commentators appear to have followed Naughtin's cue, and now also mention Wilkins when discussing the origins of the metric system.<ref>{{cite journal | ||
| |journal = International Journal of Applied Science and Technology | |journal = International Journal of Applied Science and Technology | ||
| |title = No Child Left Behind: Teaching the Metric System in US Schools | |title = No Child Left Behind: Teaching the Metric System in US Schools | ||
Revision as of 23:49, 30 December 2012
For a topical guide, see Outline of the metric system.
The origins of the metric system date back to the sixteenth century when Simon Stevin published details of his decimal notation, and the seventeenth century when John Wilkins published a proposal for a decimal system of measurement based on natural units. The first practical realisation of the metric system came during the French Revolution, when the existing system of measure which had fallen into disrepute was replaced by a decimal system based on the kilogram and the metre. The metric system was, in the words of philosopher and mathematician Condorcet, "for all people for all time". The unit of length, the metre, was based on the dimensions of the earth, and the unit of mass, the kilogram, was based on the mass of water having a volume of one litre or one thousandth of a cubic metre. Reference copies for both units were manufactured and placed in the custody of the French Academy of Sciences.
During the first half of the nineteenth century, the metric system was adopted by the scientific community. In the middle of the century, James Clerk Maxwell put forward the concept of a coherent system where a small number of units of measure were defined as base units, and all other units of measure, called derived units, were defined in terms of the base units. Maxwell proposed three base units – length, mass and time. This concept worked well with mechanics, but attempts to describe electromagnetic forces in terms of these units were beset with difficulties. By the end of the nineteenth century, four principal variants of the metric system were in place for the measurement of electromagnetic phenomena, three based on the centimetre-gram-second system of units (CGS system), and one on the metre-kilogram-second system of units (MKS system). This impasse was resolved by Giovanni Giorgi, who in 1901 proved that a coherent system that incorporated electromagnetic units had to have an electromagnetic unit as the fourth base unit.
Until 1875, the French government owned the prototype metre and kilogram, but in that year the Convention of the metre was signed, and control of the standards relating to mass and length passed to a trio of inter-governmental organisations, the senior of which was the General Conference on Weights and Measures (in French the Conférence générale des poids et mesures or CGPM). During the first half of the twentieth century, the CGPM cooperated with a number of other organisations, and by 1960 it had responsibility for defining temporal, electrical, thermal, molecular and luminar measurements, while other international organisations continued their roles in how these units of measurement were used.
In 1960, the CGPM launched the International System of Units (in French the Système international d'unités or SI) which had six base units, the metre, kilogram, second, ampere, degree kelvin (subsequently renamed the "kelvin") and candela, and 22 derived units. The mole was added as a seventh base unit in 1971. During this period, the metre was redefined in terms of the wavelength of the waves from a particular light source, and the second was defined in terms of the frequency of radiation from another light source. By the end of the century, work was well under way to redefine the ampere, kilogram, mole and kelvin in terms of the basic constants of physics, thereby ensuring that all the base units were in theory available to everybody. It is expected that this work will be completed by 2014.
Universal measure
In the early ninth century, Charlemagne introduced standard units of measure for length and for mass throughout the Holy Roman Empire. As the empire disintegrated these standards diverged and by the seventeenth century there were numerous units of measure within regions and different sizes having the same name across regions. The variations were promoted by local vested interests but hindered trade and taxation.
In 1586, the Flemish mathematician Simon Stevin published a small pamphlet called De Thiende ("the tenth"). Decimal fractions had been employed for the extraction of square roots some five centuries before his time, but it was Stevin who first introduced decimal numbers in daily life in Europe. He felt that this innovation was so significant that he declared the universal introduction of decimal coinage, measures, and weights to be merely a question of time. Many twentieth century writers regarded the French cleric Gabriel Mouton as the originator of the metric system, but in 2007 the late Pat Naughtin, a tireless metrication promoter from Australia, offered an interpretation of a few pages in a larger book by the English cleric John Wilkins (published two years before the publication of Mouton's book) suggesting that Wilkins had pre-empted the invention of the metric system by more than a century. Some commentators appear to have followed Naughtin's cue, and now also mention Wilkins when discussing the origins of the metric system.
Wilkins

Writing in An Essay towards a Real Character and a Philosophical Language, in 1668, John Wilkins, first secretary of the Royal Society proposed the concept of a "universal measure" and associated system of units based on a decimal system and natural phenomena. Tito Livio Burattini backed the proposal when he promoted the "metro cattolico" from which the word metre was to be derived. Wilkins' proposed a "seconds pendulum" (a pendulum with a half-period of one second) as the unit of length: such pendulums had recently been demonstrated by Christiaan Huygens, and their length is very close to one modern metre (as well as to length units which were then in use, such as the yard). However, it was soon discovered that the length of a seconds pendulum varies from place to place: French astronomer Jean Richer had measured the 0.3% difference in length between Cayenne (in French Guiana) and Paris. Wilkins completed the system of measurement by proposing that area and volume should be expressed as terns of the square or the cube of the "universal measure" and that the base unit of mass should be derived from the volume of a cube of rainwater with sides equal to the "universal measure". In the words of Naughtin, "... he had every single element of the modern metric system" .
Mouton
In 1670, Gabriel Mouton, a French abbot and scientist, proposed a decimal system of measurement of length based on the circumference of the Earth. His suggestion was a unit, the milliare, be defined as a minute of arc along a meridian. He then suggested a system of sub-units, dividing successively by factors of ten into the centuria, decuria, virga, virgula, decima, centesima, and millesima. His ideas attracted interest at the time, and were supported by both Jean Picard and Christiaan Huygens in 1673, and also studied at the Royal Society in London. In the same year, Gottfried Leibniz independently made proposals similar to those of Mouton.
Leading up to the French Revolution
Whereas in England the Magna Carta in 1215 decreed that "there shall be one unit of measure throughout the realm", France had a multitude of units of measure. It has been estimated that on the eve of the Revolution a quarter of a million different units of measure were in use in France; in many cases the quantity associated with each unit of measure differed from town to town and even from trade to trade. Although certain standards, such as the pied du roi (the King's foot) had a degree of pre-eminence and were used by scientists, many traders chose to use their own measuring devices, giving scope for fraud and hindering commerce and industry.
By the mid eighteenth century the need for standardisation of weights and measures had become apparent - Spain aligned her units of measure with the royal units of France, and Peter the Great aligned the Russian units of measure with the English units. In 1783 the British inventor James Watt who was having difficulties in communicating with German scientists called for the creation of a global decimal measurement system.

In 1789 the French finances were in a perilous state and in May Louis XVI summoned the Estates General. On 14 July 1789, the mob stormed the Bastille and in August 1789 the nobility surrendered their privileges, including the right to control local weights and measures. Louis XVI charged a group of experts including such notables as Lavoisier, Condorcet, Laplace, Borda and Legendre to produce the system of measures that would replace the disparate system then in place.
There was also a wish that the units of measure should be not dependent on an artifact owned by any one particular nation. Talleyrand, at the prompting of the mathematician Condorcet, approached the British and the Americans in the early 1790s with proposals of a joint effort to define the metre using the length of a pendulum (as proposed by Wilkins) as the basis of the standard of length. On 13 July 1790 Thomas Jefferson presented to Congress a document Plan for Establishing Uniformity in the Coinage, Weights, and Measures of the United States in which he advocated a decimal system that used traditional names for units (such as ten inches per foot). The report was considered but not adopted by Congress. The proposal also received the support of the British Parliament, championed by John Riggs Miller, but when the French overthrew their monarchy and decided to use the meridional definition of the metre as their base unit, Britain withdrew support.
Talleyrand resurrected the idea of the seconds pendulum before the Constituent Assembly in 1790, suggesting that the new measure be defined at 45°N (a latitude that, in France, runs just north of Bordeaux and just south of Grenoble): despite the support of the Assembly, and of Great Britain and the newly independent United States, nothing came of Talleyrand's proposal. The French Revolution and subsequent Napoleonic Wars marked the end of the Age of Enlightenment. The forces of change that had been brewing manifest themselves across all of France, including the way in which units of measure should be defined. The scientists of the day favoured the use of a system of units that were inter-related and which used a decimal basis.
Revolutionary France (1795 - 1812)

Overtures made by the French government to the British and American governments for the establishment of a common system of weights and measures came to nothing and France decided to "go it alone".
Decimal time (1793)
Decimal time was introduced in the decree of 5 October 1793 under which the day was divided into 10 "decimal hours", the "hour" into 100 " decimal minutes" and the "decimal minute" into 100 "decimal seconds". The "decimal hour" corresponded to 2 hr 24 min, the "decimal minute" to 1.44 min and the "decimal second" to 0.864 s. The revolutionary week was 10 days, but there were still twelve months in a year. The use of decimal time proved very unpopular, especially the ten day week and the calendar was officially discarded by Napoleon in 1806.
Draft metric system (1795)
The implementation of decimal time proved an immense task and under the article 22 of the law of 18 Germinal, Year III (7 April 1795), the use of decimal time was no longer mandatory. On 1 January 1806, France reverted to the traditional timekeeping.

The metric system of measure was first given a legal basis in 1795 by the French Revolutionary government. Article 5 of the law of 18 Germinal, Year III (7 April 1795) defined five units of measure. The units and their preliminary values were:
- The metre, for length - defined as being one ten millionth of the distance between the North Pole and the Equator through Paris
- The are (100 m) for area
- The stère (1 m) for volume of firewood
- The litre (1 dm) for volumes of liquid
- The gram, for mass - defined as being the mass of one cubic centimetre of water
Decimal multiples and submultiples of these units would be defined by Greek prefixes - "myria", "kilo", "hecta" (100), "deka", "deci", "centi" and "milli". Using Cassini's survey of 1744, a provisional value of 443.44 lignes was assigned to the metre which, in turn, defined the other units of measure.
The final value of the metre had to wait until 1799 when Delambre and Mechain presented the results of their survey between Dunkirk and Barcelona which fixed the length of the metre at 443.296 lignes. The law 19 Frimaire An VIII (10 December 1799) defined the metre in terms of this value and the kilogram as being 18827.15 grains. These definitions enabled reference copies of the kilograms and metres to be constructed that were to used as standards for the next 90 years.
At the same time, a new decimal-based system for angular measurement was implemented. The right angle was divided into 100 grads which in turn was divided in 100 centigrads. An arc on the earth’s surface formed by an angle of one centigrade was one kilometre. The use of the centigrade was adopted for general use in a number countries and in 1948 the General Conference on Weights and Measures (CGPM) recommended that the degree centigrade (used for the measurement of temperature) be renamed the degree Celsius.
Meridianal definition

The question of measurement reform was placed in the hands of the Academy of Sciences who appointed a commission chaired by Jean-Charles de Borda. Borda could be said to have been a fanatic for decimalization: he had invented the "repeating circle", a surveying instrument which allowed a much-improved precision in the measurement of angles between landmarks, but insisted that it be calibrated in "grades" (1⁄100 of a quarter-circle) rather than degrees, with 100 minutes to a grade and 100 seconds to a minute. For Borda, the seconds pendulum was a poor choice for a standard because the second (as a unit of time) was insufficiently decimal: he preferred a system of 10 hours to the day, 100 minutes to the hour and 100 seconds to the minute...
Instead, the commission – whose members included Lagrange, Laplace, Monge and Condorcet – decided that the new measure should be equal to one ten-millionth of the distance from the North Pole to the Equator (the quadrant of the Earth's circumference), measured along the meridian passing through Paris. Apart from the obvious nationalistic considerations, the Paris meridian was also a sound choice for practical scientific reasons: a portion of the quadrant from Dunkerque to Barcelona (about 1000 km, or one-tenth of the total) could be surveyed with start- and end-points at sea level, and that portion was roughly in the middle of the quadrant, where the effects of the Earth's oblateness were expected to be the largest.

The task of surveying the meridian arc fell to Pierre Méchain and Jean-Baptiste Delambre, and armed with letters of authorisation signed by Louis XVI the task took more than six years (1792–98). In the meantime, the commission calculated a provisional value from older surveys of 443.44 lignes.
The project was split into two parts - the northern section of 742.7 km from the Belfry, Dunkirk to Rodez Cathederal which was surveyed by Delambre and the southern section of 333.0 km from Rodez to the Montjuïc Fortress, Barcelona which was surveyed by Méchain.
Delambre used a baseline of about 10 km in length along a straight road, located close to Melun. In an operation taking six weeks, the baseline was accurately measured using four platinum rods, each of length two toise (about 3.9 m). Thereafter he used, where possible, the triangulation points used by Cassini in his 1744 survey of France. Méchain's baseline, of a similar length, and also on a straight section of road was in the Perpignan area. Although Méchain's sector was half the length of Delambre, it included the Pyrenees and hitherto unsurveyed parts of Spain. After the two surveyors met, each computed the other's baseline in order to cross-check their results and they then recomputed the kilometre. Their result came out at 0.144 lignes shorter than the provisional value, a difference of about 0.03%.

Mètre des Archives
While Méchain and Delambre were completing their survey, the commission had ordered a series of platinum bars to be made based on the provisional metre. When the final result was known, the bar whose length was closest to the meridianal definition of the metre was selected and placed in the National Archives on 22 June 1799 (4 messidor An VII in the Republican calendar) as a permanent record of the result: this standard metre bar became known as the mètre des Archives.
The metric system, that is the system of units based on the metre, was officially adopted in France on 10 December 1799 (19 frimaire An VIII) and became the sole legal system of weights and measures from 1801.
It soon became apparent that Méchain and Delambre's result (443.296 lignes) was slightly too short for the meridianal definition of the metre. Arago and Biot extended the survey to the island of Formentera in the western Mediterranean Sea in 1806–9, and found that one ten-millionth of the Earth's quadrant should be 443.31 lignes: later work increased the value to 443.39 lignes. The modern value, for the WGS 84 reference spheroid, is 1.000 196 57 m or 443.383 08 lignes.
Nevertheless, the mètre des Archives remained the legal and practical standard for the metre in France, even once it was known that it did not exactly correspond to the meridianal definition. When, in 1867, it was proposed that a new international standard metre be created, the length was taken to be that of the mètre des Archives "in the state in which it shall be found".
Kilogramme des Archives
A grave is a metallic reference standard of one thousand grams that was used for a few years until it was replaced by the kilogram standard in 1799.
On 7 April 1795, the “gramme”, upon which the kilogram is based, was decreed to be equal to “the absolute weight of a volume of pure water equal to a cube of one hundredth of a metre, and at the temperature of the melting ice”. Although this was the definition of the gram, the regulation of trade and commerce required a “practical realisation”: a single-piece, metallic reference standard that was one thousand times more massive that would be known as “grave” (symbol G). This mass unit, whose name is derived from the word “gravity”, defined by Lavoisier and René Just Haüy had been in use since 1793. Notwithstanding that the definition of the base unit of mass was the gramme (alternatively “gravet”), this new, practical realisation would ultimately become the base unit of mass. A provisional kilogram standard was made and work was commissioned to determine precisely how massive a cubic decimetre (later to be defined as equal to one litre) of water was.
Although the decreed definition of the kilogram specified water at 0 °C — a highly stable temperature point — the scientists tasked with producing the new practical realisation chose to redefine the standard and perform their measurements at the most stable density point: the temperature at which water reaches maximum density, which was measured at the time as 4 °C. They concluded that one cubic decimetre of water at its maximum density was equal to 99.92072% of the mass of the provisional kilogram made earlier that year. Four years later in 1799, an all-platinum standard, the “Kilogramme des Archives”, was fabricated with the objective that it would equal, as close as was scientifically feasible for the day, to the mass of cubic decimetre of water at 4 °C. The kilogram was defined to be equal to the mass of the Kilogramme des Archives and this standard stood for the next ninety years.
Note that the new metric system did not come into effect until after the French Revolution, when the new revolutionary government captured the idea of the metric system. The decision of the Republican government to name this new unit the “kilogramme” had been mainly politically motivated, because the name “grave” was at that time considered politically incorrect as it resembled the aristocratic German title of the Graf, an alternative name for the title of Count that, like other nobility titles, was inconsistent with the new French Republic notion of equality (égalité). Accordingly, the name of the original, defined unit of mass, “gramme”, which was too small to serve as a practical realisation, was adopted and the new prefix “kilo” was appended to it to form the name “kilogramme”. Consequently, the kilogram is the only SI base unit that has an SI prefix as part of its unit name.
Worldwide adoption of the metric system
During the nineteenth century the metric system proved a convenient political compromise during the unification processes in the Netherlands, Germany and Italy. Spain found it expedient in 1858 to follow the French example and within a decade Latin America had also adopted the metric system. There was considerable resistance to metrication in the United Kingdom and in the United States, though once the United Kingdom announced its metrication program in 1965, the Commonwealth followed suit.
France: Mesures usuelles (1812 - 1839)
Main article: Mesures usuellesThe introduction of the metric system into France in 1795 was done on a district by district basis with Paris being the first district, but it was, in terms of modern standards, poorly managed. Although thousands of pamphlets were distributed, the Agency of Weights and Measures who oversaw the introduction underestimated the work involved. Paris alone needed 500,000 metre sticks, yet one month after the metre became the sole legal unit of measure, they only had 25,000 in store. This, combined with other excesses of the Revolution and the high level of illiteracy made the metric system unpopular.
Napoleon himself ridiculed the metric system, but as an able administrator, recognised the value of a sound basis for a system of measurement and under the décret impérial du 12 février 1812 (imperial decree of 12 February 1812), a new system of measure - the mesure uselles or "customary measures" was introduced for use in small retail businesses - all government, legal and similar works still had to use the metric system and the metric system continued to be taught at all levels of education. The names of many units used during the ancien regime were reintroduced, but were redefined in terms of metric units. Thus the toise was defined as being two metres with six pied making up one toise, twelve pouce making up one pied and twelve lignes making up one pouce. Likewise the livre was defined as being 500 g, each livre comprising sixteen once and each once eight gros and the aune as 120 centimetres.
The Dutch metric system
The Netherlands first used the metric system and then, in 1812, the mesures usuelles when it was part of the First French Empire. Under the Royal decree of 27 March 1817 (Koningklijk besluit van den 27 Maart 1817), the newly-formed Kingdom of the Netherlands abandoned the mesures usuelles in favour of the "Dutch" metric system (Nederlands metrisch stelsel) in which metric units were given the names of units of measure that were then in use. Examples include the ons (ounce) which was defined as being 100 g:
The German Zollverein

At the outbreak of the French Revolution, much of modern-day Germany and Austria were part of the Holy Roman Empire which has become a loose federation of kingdoms, principalities, free cities, bishoprics and other fiefdoms, each with its own system of measurement, though in most cases such system were loosely derived from the Carolingian system instituted by Charlemagne a thousand years earlier.
During the Napoleonic era, there was a move among some of the German states to reform their systems of measurement using the prototype metre and kilogram as the basis of the new units. Baden, in 1810, for example, redefined the ruthe (rods) as being 3.0 m exactly and defined the subunits of the ruthe as 1 ruthe = 10 fuβ (feet) = 100 zoll (inches) = 1,000 linie (lines) = 10,000 punkt (points) while the pfund was defined as being 500 g, divided into 30 loth, each of 16.67 g. Bavaria, in its reform of 1811, trimmed the Bavarian pfund from 561.288 g to 560 g exactly, consisting of 32 loth, each of 17.5 g while the Prussian pfund remained at 467.711 g.
After the Congress of Vienna there was a degree of commercial cooperation between the various German states resulting in the setting of the German Customs Union (Zollverein). There were however still many barriers to trade until Bavaria took the lead in establishing the General German Commercial Code in 1856. As part of the code the Zollverein introduce the Zollpfund (Customs Pound) which was defined to be exactly 500 g and which could be split into 30 'lot'. This unit was used for inter-state movement of goods, but was not applied in all states for internal use.
Although the Zollverein collapsed after the Austro-Prussian War of 1866, the metric system became the official system of measurement in the newly formed German Empire in 1871 and of Austria in 1875. The Zollpfund ceased to be legal in Germany after 1877.
Italy

The Cisalpine Republic, a North Italian republic set up by Napoleon in 1797 with its capital at Milan first adopted a modified form of the metric system based in the braccio cisalpino (Cisalpine cubit) which was defined to be half a metre. In 1802 the Cisalpine Republic was renamed the Italian Republic, with Napoleon as its head of state. The following year the Cisalpine system of measure was replaced by the metric system.
In 1806, the Italian Republic was replaced by the Kingdom of Italy with Napoleon as its emperor. By 1812, all of Italy from Rome northwards was under the control of Napoleon, either as French Departments or as part of the Kingdom of Italy ensuring the metric system was in use throughout this region.
After the Congress of Vienna, the various Italian states reverted to their original system of measurements, but in 1845 the Kingdom of Piedmont and Sardinia passed legislation to introduce the metric system within five years. By 1860, most of Italy had been unified under the King of Sardinia Victor Emmanuel II and under Law 132 of 28 July 28, 1861 the metric system became the official system of measurement throughout the kingdom. Numerous Tavole di ragguaglio (Conversion Tables) were displayed in shops until 31 December 1870.
Spain
Until the ascent of the Bourbon monarchy in Spain in 1700, each of the regions of Spain retained their own system of measurement. The new Bourbon monarchy tried to centralise control and with it the system of measurement. There were debates regarding the desirability of retaining the Castilian units of measure or, in the interests of harmonisation, adopting the French system. Although Spain assisted Machain in his meridian survey, the Government feared the French revolutionary movement and reinforced the Castilian units of measure to counter such movements. By 1849 however, it proved difficult to maintain the old system and in that year the metric system became the legal system of measure in Spain.
United Kingdom and the Commonwealth
Main articles: Metrication in the United Kingdom and Metrication of British TransportIn 1824 the Weights and Measures Act imposed one standard 'imperial' system of weights and measures on the British Empire. The effect of this act was to standardise existing British units of measure rather than to align them with the metric system.
During the next eighty years a number of Parliamentary select committees recommended the adoption of the metric system each with a greater degree of urgency, but Parliament prevaricated. A Select Committee report of 1862 recommended compulsory metrication, but with an "Intermediate permissive phase", Parliament responded in 1864 by legalising metric units only for 'contracts and dealings'. Initially the United Kingdom declined to sign the Treaty of the Metre, but did so in 1883. Meanwhile British scientists and technologists were at the forefront of the metrication movement - it was the British Association for the Advancement of Science that promoted the cgs system of units as a coherent system and it was the British firm Johnson Matthey that was accepted by the CGPM in 1889 to cast the international prototype metre and kilogram.
In 1895 another Parliamentary select committee recommended the compulsory adoption of the metric system after a two-year permissive period, the 1897 Weights and Measures Act legalised the metric units for trade, but did not make them mandatory. A bill to make the metric system compulsory in order to enable British industrial base to fight off the challenge of the nascent German base passed through the House of Lords in 1904, but did not pass in the House of Commons before the next general election was called. Following opposition by the Lancashire cotton industry, a similar bill was defeated in 1907 in the House of Commons by 150 votes to 118.
In 1965 Britain commenced an official program of metrication that, as of 2012, had not been completed. The British metrication program signaled the start of metrication programs elsewhere in the Commonwealth, though India had started her program before in 1959, six years before the United Kingdom. South Africa (then not a member of the Commonwealth) set up a Metrication Advisory Board in 1967, New Zealand set up its Metric Advisory Board in 1969, Australia passed the Metric Conversion Act in 1970 and Canada appointed a Metrication Commission in 1971. Metrication in Australia, New Zealand and South Africa was essentially complete within a decade while metrication in India and Canada is not complete. In addition the lakh and crore are still in widespread use in India. Most other Commonwealth countries adopted the metric system during the 1970s.
United States
Main article: Metrication in the United StatesThe United States government acquired copies of the French metre and kilogram for reference purposes in 1805 and 1820 respectively. In 1866 the United States Congress passed a bill making it lawful to use the metric system in the United States. The bill, which was permissive rather than mandatory in nature, defined the metric system in terms of customary units rather than with reference to the international prototype metre and kilogram. By 1893, the reference standards for customary units had become unreliable. Moreover, the United States, being a signatory of the Metre Convention was in possession of national prototype metres and kilograms that were calibrated against those in use elsewhere in the world. This led to the Mendenhall Order which redefined the customary units by referring to the national metric prototypes, but used the conversion factors of the 1866 act. In 1896 a bill that would make the metric system mandatory in the United States was presented to Congress. Of the 29 people who gave evidence before the congressional committee who were considering the bill, 23 were in favour of the bill, but six were against. Four of the six dissenters represented manufacturing interests and the other two the United States Revenue service. The grounds cited were the cost and inconvenience of the change-over. Subsequent bills suffered a similar fate.
Development of a coherent metric system
From its inception, the metric system was designed in such a manner that the various units of measure were linked to each other. At the start of the nineteenth century, length, mass and temperature were the only base units that had been standardised. The beginnings of a coherent system were in place with the units of area and volume linked to the unit of length, though at the time science did not understand the concepts of base units and derived units, nor how many physical quantities were inter-related.
Time, work and energy
In 1832 Carl-Friedrich Gauss made the first absolute measurements of the Earth's magnetic field using a decimal system based using the millimetre, gram, and second as the units of measure for length, mass, and time respectively, thereby implicitly making time a base dimension of the metric system.

In a paper published in 1843, James Prescott Joule first demonstrated a means of measuring the energy transferred between different systems when work is done thereby relating Nicolas Clément's calorie, defined in 1824, to mechanical work. Energy became the unifying concept of nineteenth century science, initially by bringing thermodynamics and mechanics together and electrical technology and ultimately relativistic physics leading to Einstein's equation . The CGS unit of energy was the "erg", but the SI unit of energy was named the "joule" in honour of Joule.
In 1861 a committee of the British Association for Advancement of Science (BAAS) including William Thomson (later Lord Kelvin), James Clerk Maxwell and Joule among its members was tasked with investigating the "Standards of Electrical Resistance". In their first report (1862) they laid the ground rules for their work - the metric system was to be used, measures of electrical energy must have the same units as measures of mechanical energy and two sets of electromagnetic units would have to be derived - an electromagnetic system and an electrostatic system. In the second report (1863) they introduced the concept of a coherent system of units whereby units of length, mass and time were identified as "fundamental units" (now known as base units). All other units of measure could be derived (hence derived units) from these base units. The metre, gram and second were chosen as base units.
In 1873, another committee of the BAAS that also counted Maxwell and Thomson among its members and tasked with "the Selection and Nomenclature of Dynamical and Electrical Units" recommended using the CGS (centimetre-gram-second) system of units. The committee also recommended the names of "dyne" and "erg" for the CGS units of force and energy. The CGS system became the basis for scientific work for the next seventy years.
Electrical units
In the 1820s Georg Ohm formulated Ohms Law which can be extended to relate power to current, potential difference (voltage) and resistance. During the following decades the realisation of a coherent system of units that incorporated the measurement of electromagnetic phenomena and Ohm's law was beset with problems - at least four different systems of units were devised. In the three CGS systems, the constants and and consequently and were dimensionless.
Symbols used in this section
|
Electromagnetic system of units- In 1820s André-Marie Ampère discovered a relationship between the force between two current-carrying conductors, now known as Ampere's law which can be written
- where (SI units)
- In 1833 Gauss pointed out the possibility of equating this force with its mechanical equivalent. This proposal received further support from Wilhelm Weber in 1851. The electromagnetic (or absolute) system of units was one of the two systems of units identified in the BAAS report of 1862 and defined in the refport of 1873. In this system, current is defined by setting the magnetic force constant to unity and potential difference is defined in such a way as to ensure the unit of power calculated by the relation is identical to the unit of power required to move a mass of one gram a distance of one centimetre in one second when opposed by a force of one dyne. The electromagnetic units of measure were known as the abampere, the abvolt, the abcoulomb and so on.
- Electrostatic system of units
- In 1783 Coulomb discovered and published the relationship between the force exerted between two charged bodies. This relationship, now known as Coulomb's law can be written
- where (SI units)
- The electrostatic system was the second of the two systems of units identified in the 1862 BAAS report and defined in the report of 1873. In this system unit for charge is defined by setting the Coulomb force constant () to unity and the unit for potential difference were defined to ensure the unit of energy calculated by the relation is one erg. The electrostatic units of measure are now known as the statampere, the statvolt, the statcoulomb and so on.
- Gaussian system of units
- In 1888 Heinrich Hertz verified Maxwell's Equations and in so doing realised that the CGS system of electromagnetic units to were related to the CGS system of electrostatic units by the relationship:
- Using this relationship, he proposed merging the EMU and the ESU systems into one system using the EMU units for magnetic quantities (subsequently named the gauss and maxwell) and ESU units elsewhere. He named this combined set of units "Gaussian units". This set of units has been recognised as being particularly useful in theoretical physics.International Bureau of Weights and Measures (2006), The International System of Units (SI) (PDF) (8th ed.), ISBN 92-822-2213-6, archived (PDF) from the original on 2021-06-04, retrieved 2021-12-16
- Practical system of units
- The CGS units of measure used in scientific work were not practical when used in engineering leading to the development of the practical system of electric units. At the time that this system of units was proposed, the dimensions of electrical resistance was modelled as the ratio of length to time (ie a velocity). The most practical unit for resistance was multiples of 10 m/s - the base unit of length was the length of the Earth's quadrant, the base unit of time the second and the base unit of mass was 10 g, the latter having been chosen to allow conversion back to the CGS system. The names, but not the values, amp, volt, farad and ohm were carried over from the CGS system. The system was adopted at the International Electrical Congress (IEC) in 1881. This system was formalised as the International System of Electrical and Magnetic Units at the 1893 congress of the IEC in Chicago where the volt, amp and ohm were formally defined. The SI units with these names are very close, but not identical to the "practical units".
A coherent system
The electrical units of measure did not easily fit into the coherent system using length, mass and time as its base units as proposed in the 1861 BAAS paper. Using dimensional analysis the dimensions of charge as defined by the ESU system of units was identical to the dimensions of current as defined by the EMU system of units while resistance had the same dimensions as velocity in the EMU system of units, but had the dimensions of the inverse of velocity in the ESU system of units.
From mid 1890s onwards Giovanni Giorgi and Oliver Heaviside corresponded with each other regarding these anomalous results. This led to Giorgi presenting a paper to the congress of the Associazione Elettrotecnica Italiana (A.E.I.) in October 1901 in which he showed that a coherent electro-mechanical system of units could be obtained by adding a fourth base unit of an electrical nature (ampere, volt or ohm) to the three base units proposed in the 1861 BAAS report. This gave the constants ke and km physical dimensions and hence the electrco-mechanical quantities ε0 and µ0 were also given physical dimensions.
It took more than thirty years before Giorgi's work was accepted in practice by international organisations and nearly another thirty years before they were incorporated as the basis of the Système International d'Unités (International System of Units), the SI.
Naming the units of measure
In 1861, Charles Bright and Latimer Clark proposed the names of ohm, volt, and farad in honour of Georg Ohm, Alessandro Volta and Michael Faraday respectively for the practical units based on the centimetre-gramme-second absolute system. This was supported by Thomson (Lord Kelvin) These names were later scaled for use in the Practical System. The concept of naming units of measure after noteworthy scientists was subsequently used for other units.
Convention of the metre
Main article: Metre Convention
With increasing international adoption of the metre, the short-comings of the mètre des Archives as a standard became ever more apparent. Countries which adopted the metre as a legal measure purchased standard metre bars that were intended to be equal in length to the mètre des Archives, but there was no systematic way of ensuring that the countries were actually working to the same standard. The meridianal definition, which had been intended to ensure international reproducibility, quickly proved so impractical that is was all but abandoned in favour of the artifact standards, but the mètre des Archives (and most of its copies) were "end standards": such standards (bars which are exactly one metre in length) are prone to wear with use, and different standard bars could be expected to wear at different rates.
The International Conference on Geodesy in 1867 called for the creation of a new, international prototype metre and to arrange a system where national standards could be compared with it. The international prototype would also be a "line standard", that is the metre was defined as the distance between two lines marked on the bar, so avoiding the wear problems of end standards. The French government gave practical support to the creation of an International Metre Commission, which met in Paris in 1870 and again in 1872 with the participation of about thirty countries.
On 20 May 1875 an international treaty known as the Convention du Mètre (Metre Convention) was signed by 17 states. This treaty established the following organisations to conduct international activities relating to a uniform system for measurements:

- Conférence générale des poids et mesures (CGPM), an intergovernmental conference of official delegates of member nations and the supreme authority for all actions;
- Comité international des poids et mesures (CIPM), consisting of selected scientists and metrologists, which prepares and executes the decisions of the CGPM and is responsible for the supervision of the International Bureau of Weights and Measures;
- Bureau international des poids et mesures (BIPM), a permanent laboratory and world centre of scientific metrology, the activities of which include the establishment of the basic standards and scales of the principal physical quantities, maintenance of the international prototype standards and oversight of regular comparisons between the international prototype and the various national standards.
The international prototype metres and kilograms were both made from a 90% platinum, 10% iridium alloy which is exceptionally hard and which has good electrical and thermal conductivity properties. The prototype had a special X-shaped (Tresca) cross section to minimise the effects of torsional strain during length comparisons. and the prototype kilograms were cylindrical in shape. The London firm Johnson Matthey delivered 30 prototype metres and 40 prototype kilograms. At the first meeting of the CGPM in 1889 bar No. 6 and cylinder No. X were accepted as the international prototypes. The remainder were either kept as BIPM working copies or distributed to member states as national prototypes.
Twentieth century
At the beginning of the twentieth century, the BIPM had custody of two artifacts - one to define length and the other to define mass. Other units of measure which did not rely on specific artifacts were controlled by other bodies. In the scientific world, quantum theory was in its infancy and Einstein had yet to publish his theories of relativity. By the end of the century, a coherent system of units was in place under the control of the bodies set up by the Treaty of the Metre, the definition of the second relied on quantum theory, the definition of the metre relied on the theory of relativity and plans were being made to relegate the international prototype kilogram to the archives.
Metre
The first (and only) follow-up comparison of the national standards with the international prototype metre was carried out between 1921 and 1936, and indicated that the definition of the metre was preserved to within 0.2 µm. During this follow-up comparison, the way in which the prototype metre should be measured was more clearly defined—the 1889 definition had defined the metre as being the length of the prototype at the definition of melting ice, but in 1927 the 7th CGPM extended this definition was to specify that the prototype metre shall be "supported on two cylinders of at least one centimetre diameter, symmetrically placed in the same horizontal plane at a distance of 571 mm from each other". The choice of 571 mm represents the Airy points of the prototype—the points at which the bending or droop of the bar is minimized.
In 1887 Michelson proposed the use of optical interferometers for the measurement of length, work which contributed to him being awarded the Nobel Prize in 1907. In 1952 the CIPM proposed the use of wavelength of a specific light source as the standard for defining length and in 1960 the CGPM accepted this proposal using radiation corresponding to a transition between specified energy levels of the krypton 86 atom as the new standard for the metre. By 1975, when the second had been defined in terms of a physical phenomena rather than the earth's rotation and Einstein's assertion that the speed of light was constant, the CGPM authorised the CIPM to investigate the use of the speed of light as the basis for the definition of the metre. This proposal was accepted in 1983.
Kilogram
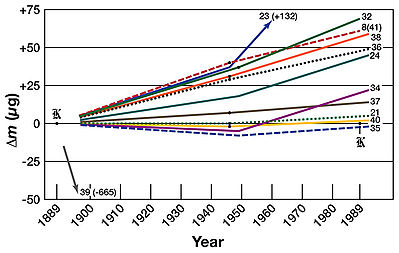
Although the definition of the kilogram remained unchanged throughout the twentieth century, the 3rd CGPM in 1901 clarified that the kilogram was a unit of mass, not of weight. The original batch of 40 prototypes (adopted in 1889) were supplemented from time to time with further prototypes for use by new signatories to the Metre Convention.
During the course of the century, the various national prototypes of the kilogram were recalibrated against the international prototype and therefore against each other. The initial 1889 starting-value offsets of the national prototypes relative to the IPK were nulled. and any subsequent mass changes being relative to the IPK. A technique for steam cleaning the prototypes to remove any contaminants was developed in 1946 as part of the second recalibration.
The third periodic recalibration in 1988-9 revealed that the average difference between International Prototype Kilogram and adjusted baseline for the national prototypes was 50 μg - in 1889 the baseline of the national prototypes had been adjusted so that the difference was zero. As the IPK is the definitive kilogram, there is no way of telling whether the IPK had been losing mass or the national prototypes had been gaining mass.
Time
Until the advent of the atomic clock, the most reliable timekeeper available to mankind was the earth's rotation. It was natural therefore that the astronomers under the auspice of the International Astronomical Union (IAU) took the lead in maintaining the standards relating to time. During the twentieth century it became apparent that the earth's rotation was slowing down resulting in days becoming 1.4 milliseconds longer each century - this was verified by comparing the calculated timings of eclipses of the sun with those observed in antiquity going back to Chinese records of 763 BC.
In 1956 the 10th CGPM instructed the CIPM to prepare a definition of the second; in 1958 the definition was published stating that the second would be calculated by extrapolation using earth's rotational speed in 1900. Astronomers from the US Naval Observatory (USNO) and the National Physical Laboratory determined a relationship between the frequency of radiation corresponding to the transition between the two hyperfine levels of the ground state of the cesium 133 atom and the estimated rate of rotation of the earth in 1900. Their value was adopted in 1968 by the 13th CGPM.
Electrical units

In 1921 the Treaty of the Metre was extended to cover electrical units with the CGPM merging its work with that of the IEC. At the 8th CGPM in 1933 the need to replace the "International" electrical units with "absolute" units was raised. The IEC proposal that Giorgi's proposal be adopted was accepted, but no decision was made as to which electrical unit should be the fourth base unit. In 1935 Sears proposed that this should be the ampere, but World War II prevented this being formalised until 1946. The definitions for absolute electrical system became effective from 1 January 1948.
Temperature
At the start of the twentieth century, the fundamental macroscopic laws of thermodynamics had been formulated and although techniques existed to measure temperature using empirical techniques, the scientific understanding of the nature of temperature was minimal. Maxwell and Boltzmann had produced theories describing the inter-relational of temperature, pressure and volume of a gas on a microscopic scale but otherwise, in 1900, there was no understanding of the microscopic or quantum nature of temperature. Within the metric system, temperature was expressed in degrees Centigrade with the definition that ice melted at 0 °C and at standard atmospheric pressure, water boiled at 100 °C. A series of lookup tables defined temperature in terms of inter-related empirical measurements made using various devices.
When, in 1948 the CGPM was charged with producing a coherent system of units of measure, definitions relating to temperature had to be clarified. At the 9th CGPM, the centigrade temperature scale was renamed the celsius temperature scale and the scale itself was fixed by defining the triple point of water as 0.01 °C, though the CGPM left the formal definition of absolute zero until the 10th GCPM when the name "degrees Kelvin" was assigned to the absolute temperature scale and triple point of water was defined as being 273.16 °K. In 1967, at the 13th GCPM the degree Kelvin (°K) was renamed the "kelvin" (K).
Over the ensuing years, the BIPM developed and maintained cross-correlations relating various measuring devices such as thermocouples, light spectra and the like to the equivalent temperatures. Increasingly the use of the Boltzmann Relationship was used as the reference point and it appears likely that in 2015 the CGPM will redefine temperature in terms of the Boltzmann constant rather than the triple point of water.
Luminosity
Prior to 1937, the International Commission on Illumination (CIE from its French title, the Commission Internationale de l´Eclairage) in conjunction with the CIPM produced a standard for luminous intensity to replace the various national standards. This standard, the candela (cd) which was defined as "the brightness of the full radiator at the temperature of solidification of platinum is 60 new candles per square centimetre". was ratified by the GCPM in 1948 and in 1960 was adopted as an SI base unit. The definition proved difficult to implement so in 1967, the definition was revised and the reference to the radiation source was replaced by defining the candles in terms of the power of a specified wavelength of visible light.
In 2007 the CIPM and the CIE agreed a program of cooperation with the CIPM taking the lead in defining the use of units of measure and the CIE taking the lead in defining the behaviour of the human eye.
Mole
The mole was originally known as a gram-atom or a gram-molecule - the amount of a substance measured in grams divided by its atomic weight. Originally chemists and physicists had differing views regarding the definition of the atomic weight - both assigned a value of 16 atomic mass units (amu) to oxygen, but physicists defined oxygen in terms of the O isotope whereas chemists assigned 16 amu to O, O and O isotopes mixed in the proportion that they occur in nature. Finally an agreement between the International Union of Pure and Applied Physics (IUPAP) and the International Union of Pure and Applied Chemistry (IUPAC) brought this duality to an end in 1959/60, both parties agreeing to define the atomic weight of C as being exactly 12 amu. This agreement was confirmed by ISO and in 1969 the CIPM recommended its inclusion in SI as a base unit. This was done in 1971 at the 14th CGPM.
International System of Units (SI)
Main article: International System of UnitsThe 9th CGPM met in 1948, fifteen years after the 8th CGPM. In response to formal requests made by the International Union of Pure and Applied Physics and by the French government to establish a practical system of units of measure, the CGPM requested the CIPM to prepare recommendations for a single practical system of units of measurement, suitable for adoption by all countries adhering to the Metre Convention. At the same time the CGPM formally adopted a recommendation for the writing and printing of unit symbols and of numbers. The recommendation also catalogued the recommended symbols for the most important MKS and CGS units of measure and for the first time the CGPM made recommendations concerning derived units.
The CIPM's draft proposal, which was an extensive revision and simplification of the metric unit definitions, symbols and terminology based on the MKS system of units, was put to the 10th CGPM in 1954. In accordance with Giorgi's proposals of 1901, the CIPM also recommended that the ampere be the base unit from which electromechanical would be derived. The definitions for the ohm and volt that had previously been in use were discarded and these units became derived units based on the metre, ampere, second and kilogram. After negotiations with the CIS and IUPAP, two further base units, the degree kelvin and the candela were also proposed as base units. The full system and name "Système International d'Unités" were adopted at the 11th CGPM.
During the years that followed the definitions of the base units and particularly the mise en pratique to realise these definitions have been refined.
The "New SI"
Main article: New SI definitions
When the metre was redefined in 1960, the kilogram was the only SI base unit that relied on a specific artifact. Moreover, after the 1996-1998 recalibration a clear divergence between the various prototype kilograms was observed.
At its 23rd meeting (2007), the CGPM mandated the CIPM to investigate the use of natural constants as the basis for all units of measure rather than the artifacts that were then in use. At a meeting of the CCU held in Reading, United Kingdom in September 2010, a resolution and draft changes to the SI brochure that were to be presented to the next meeting of the CIPM in October 2010 were agreed to in principle. The proposals that the CCU put forward were:
- In addition to the speed of light, four constants of nature—Planck's constant, an elementary charge, Boltzmann constant and Avogadro's number be defined to have exact values.
- The international prototype kilogram be retired
- The current definitions of the kilogram, ampere, kelvin and mole be revised.
- The wording of the definitions of all the base units be tightened up
The CIPM meeting of October 2010 found that "the conditions set by the General Conference at its 23rd meeting have not yet been fully met. For this reason the CIPM does not propose a revision of the SI at the present time"; however the CIPM presented a resolution for consideration at the 24th CGPM (17–21 October 2011) to agree the new definitions in principle, but not to implement them until the details have been finalised. This resolution was accepted by the conference and in addition the CGPM moved the date of the 25th meeting forward from 2015 to 2014.
Notes
- Prototype No. 8(41) was accidentally stamped with the number 41, but its accessories carry the proper number 8. Since there is no prototype marked 8, this prototype is referred to as 8(41).
References
- ^
 This article incorporates text from a publication now in the public domain: Larousse, Pierre, ed. (1874), "Métrique", Grand dictionnaire universel du XIXe siècle, vol. 11, Paris: Pierre Larousse, pp. 163–64.
This article incorporates text from a publication now in the public domain: Larousse, Pierre, ed. (1874), "Métrique", Grand dictionnaire universel du XIXe siècle, vol. 11, Paris: Pierre Larousse, pp. 163–64.
- ^ Nelson, Robert A. (1981), "Foundations of the international system of units (SI)" (PDF), Phys. Teacher: 597.
- O'Connor, John J.; Robertson, Edmund F. (January 2004), "Simon Stevin", MacTutor History of Mathematics Archive, University of St Andrews
- McGreevy, Thomas; Cunningham, Peter (1995). The Basis of Measurement: Volume 1 - Historical Aspects. p. 140. ISBN ].
{{cite book}}: Check|isbn=value: invalid character (help); Text "0 948251 82 4" ignored (help) |publisher = Picton Publishing (Chippenham) Ltd}} - {{cite web |url=http://themetricmaven.com/?page_id=101 |title=Metrication Resources |publisher=The Metric Maven
- ^ "Aussie researcher challenges origins of metric system". ABC News. 15 July 2007. Retrieved 30 December 2012.
- Craig, Kern W. (April 2012). "No Child Left Behind: Teaching the Metric System in US Schools" (PDF). International Journal of Applied Science and Technology. 2 (4): 44 - 48. ISSN 2221-1004.
{{cite journal}}: More than one of|at=and|page=specified (help) - Dew, Nicholas (15–17 February 2008). The Hive and the Pendulum: Universal Metrology and Baroque Science (PDF). Baroque Science workshop. p. 5.
{{cite conference}}: CS1 maint: date format (link) - "Celebrating metrology: 51 years of SI units". Institute of Physics. 20 June 2011.
{{cite web}}:|access-date=requires|url=(help); Missing or empty|url=(help) - John Wilkins (1668). "VII". An Essay towards a Real Character and a Philosophical Language. The Royal Society. pp. 190–194.
{{cite book}}:|access-date=requires|url=(help)
Reproduction (33 MB); Transcription (126 kB) - Metric system 'was British'. BBC news. Retrieved 2011-03-06.
- Misura Universale, 1675.
- O'Connor, John J.; Robertson, Edmund F. (January 2004), "Christiaan Huygens", MacTutor History of Mathematics Archive, University of St Andrews
- E F Robertson, J J O'Connor. "Jean Richer". The MacTutor History of Mathematics archive. School of Mathematics and Statistics, University of St Andrews, Scotland. Retrieved 2011-03-06.
- Poynting, John Henry; Thompson, Joseph John (1907), A Textbook of Physics: Properties of Matter (4th ed.), London: Charles Griffin
{{citation}}: Unknown parameter|page Ε=ignored (help). - ^ O'Connor, John J.; Robertson, Edmund F. (January 2004), "Gabriel Mouton", MacTutor History of Mathematics Archive, University of St Andrews
- G. Bigourdan (1901). "Le système métrique des poids et des mesures" (in French). Paris. Retrieved 2011-03-25.
{{cite web}}: Unknown parameter|trans_title=ignored (|trans-title=suggested) (help) - "Magna Charta translation". National Archives and Records Administration. Retrieved 2011-03-25.
- ^ "History of measurement". Métrologie française. Retrieved 2011-02-06.
- ^ Adler, Ken (2002). The Measure of all Things - The Seven -Year-Odyssey that Transformed the World. London: Abacus. pp. 2–3. ISBN 0 349 11507 9.
{{cite book}}: Check|isbn=value: invalid character (help) - ^ Loidi, Juan Navarro; Saenz, Pilar Merino (6–9 September 2006). "The units of length in the Spanish treatises of military engineering" (PDF). The Global and the Local:The History of Science and the Cultural Integration of Europe. Proceedings of the 2nd ICESHS. Cracow, Poland: The Press of the Polish Academy of Arts and Sciences. Retrieved 2011-03-17.
{{cite web}}: CS1 maint: date format (link)> - Jackson, Lowis D'Aguilar. Modern metrology; a manual of the metrical units and systems of the present century (1882). London: C Lockwood and co. p. 11. Retrieved 2011-03-25.
- Carnegie, Andrew (May 1905). James Watt (PDF). Doubleday, Page & Company. pp. 59–60. Retrieved 20 October 2011.
- Jefferson, Thomas (4 July 1790). "Plan for Establishing Uniformity in the Coinage, Weights, and Measures of the United States; Communicated to the House of Representatives July 13, 1790". New York. Retrieved 10 November 2012.
- Alder, Ken (2002). The Measure of all Things – The Seven-Year-Odyssey that Transformed the World. London: Abacus. pp. 252–253. ISBN 0 349 11507 9.
{{cite book}}: Check|isbn=value: invalid character (help) - Adler. pp. 88–96.
{{cite book}}: Missing or empty|title=(help) - "Dials & Symbols of the French revolution. The Republican Calendar and Decimal time". The Horological Foundation. Retrieved 2011-03-07.
- ^ "Décret relatif aux poids et aux mesures. 18 germinal an 3 (7 avril 1795)". Le systeme metrique decimal (in French). Association Métrodiff. Retrieved 2011-02-07.
{{cite web}}: Unknown parameter|trans_title=ignored (|trans-title=suggested) (help) - "Dials & Symbols of the French revolution. The Republican Calendar and Decimal time". The Horological Foundation. Retrieved 2011-02-07.
- Adler. p. 106.
{{cite book}}: Missing or empty|title=(help) - Suzanne Débarbat. "Fixation de la longueur définitive du mètre" (in French). Ministère de la culture et de la communication (French ministry of culture and communications). Retrieved 2011-03-01.
{{cite web}}: Unknown parameter|trans_title=ignored (|trans-title=suggested) (help) - Smeaton, William A. (2000). "The Foundation of the Metric System in France in the 1790s: The importance of Etienne Lenoir's platinum measuring instruments" (PDF). Platinum Metals Rev. 44 (3). Ely, Cambridgeshire, United Kingdom: 125–134. Retrieved 10 November 2012.
- "CIPM, 1948 and 9th CGPM, 1948". International Bureau of Weights and Measures (BIPM). Retrieved 2011-02-08.
- Jean Charles de Borda, MacTutor, retrieved 2010-08-13.
- Adler. pp. 21–33.
{{cite book}}: Missing or empty|title=(help) - The technical difficulties were not the only problems the surveyors had to face in the convulsed period of the aftermath of the Revolution: Méchain and Delambre, and later Arago, were imprisoned several times during their surveys, and Méchain died in 1804 of yellow fever, which he contracted while trying to improve his original results in northern Spain (see Alder).
- ^ All values in lignes are referred to the toise de Pérou, not to the later value in mesures usuelles. 1 toise = 6 pieds; 1 pied = 12 pouces; 1 pouce = 12 lignes; so 864 lignes = 1 toise.
- ^ Adler. pp. 227–230.
{{cite book}}: Missing or empty|title=(help) - Distances measured using Google Earth. The coordinates are:
51°02′08″N 2°22′34″E / 51.03556°N 2.37611°E / 51.03556; 2.37611 (Belfry, Dunkirk) - Belfry, Dunkirk
44°25′57″N 2°34′24″E / 44.43250°N 2.57333°E / 44.43250; 2.57333 (Rodez Cathederal) - Rodez Cathederal
41°21′48″N 2°10′01″E / 41.36333°N 2.16694°E / 41.36333; 2.16694 (Montjuïc, Barcelona) - Montjuïc, Barcelona - Adler. pp. 240–241.
{{cite book}}: Missing or empty|title=(help) - The WGS 84 reference spheroid has a semi-major axis of 6 378 137.0 m and a flattening of 1⁄298.257 223 563.
- ^ The International Metre Commission (1870-1872), International Bureau of Weights and Measures, retrieved 2010-08-15.
- ^ The BIPM and the evolution of the definition of the metre, International Bureau of Weights and Measures, retrieved 2010-08-15.
- Poirier, Jean-Pierre. "Chapter 8: Lavoisier, Arts and Trades". Antoine-Laurent de Lavoisier (1743-1794 - Life and Works. Comité Lavoisier de l'Académie des Sciences de Paris. Retrieved 2011-08-04.
- L’Histoire Du Mètre, La Détermination De L’Unité De Poids, link to Web site here.
- History of the kilogram
- BIPM - the name "kilogram"
- Adler. p. 269.
{{cite book}}: Missing or empty|title=(help) - Denis Février. "Un historique du mètre" (in French). Ministère de l'Economie, des Finances et de l'Industrie. Retrieved 2011-03-10.
- Hallock, William; Wade, Herbert T (1906). "Outlines of the evolution of weights and measures and the metric system". London: The Macmillan Company. pp. 66–69.
- Jacob de Gelder (1824). Allereerste Gronden der Cijferkunst (in Dutch). 's Gravenhage and Amsterdam: de Gebroeders van Cleef. pp. 155–157. Retrieved 2011-03-02.
{{cite book}}: Unknown parameter|trans_title=ignored (|trans-title=suggested) (help) - ^ "Amtliche Maßeinheiten in Europa 1842" (in German). Retrieved 2011-03-26Text version of Malaisé's book
{{cite web}}: Unknown parameter|trans_title=ignored (|trans-title=suggested) (help)CS1 maint: postscript (link) - Ferdinand Malaisé (1842). Theoretisch-practischer Unterricht im Rechnen (in German). München. pp. 307–322. Retrieved 2011-03-26.
{{cite book}}: Unknown parameter|trans_title=ignored (|trans-title=suggested) (help) - Heinrich Grebenau (1870). "Tabellen zur Umwandlung des bayerischen Masses und Gewichtes in metrisches Maß und Gewicht und umgekehrt" (in German). Munich. Retrieved 2011-03-07.
{{cite web}}: Unknown parameter|trans_title=ignored (|trans-title=suggested) (help) - Silke Parras (2006). "2.1". Der Marstall des Schlosses Anholt (16. bis 18. Jahrhundert) - Quellen und Materialien zur Geschichte der Pferdehaltung im Münsterland (PDF) (Dr. med. vet thesis). Tierärztliche Hochschule Hannover . Retrieved 2011-03-07.
{{cite thesis}}: Italic or bold markup not allowed in:|publisher=(help) - ^ "Fundstück des Monats November 2006" (in German). Bundesministerium der FinanzenQuelle: www.zoll.de. 4 June 2009. Retrieved 2011-03-07.
{{cite web}}: Unknown parameter|trans_title=ignored (|trans-title=suggested) (help) - Andreas Dreizler; et al. (20 April 2009). "Metrologie" (PDF) (in German). Technische Universität Darmstaft. Retrieved 2011-03-28.
{{cite web}}: Explicit use of et al. in:|author=(help) - ^ W Leconte Stephens (March 1904). "The Metric System - Shall it be compulsory?". Popular Science Monthly: 394–405. Retrieved 2011-05-17.
- ^ Maria Teresa Borgato (6–9 September 2006). "The first applications of the metric system in Italy" (PDF). The Global and the Local:The History of Science and the Cultural Integration of Europe. Proceedings of the 2nd ICESHS. Cracow, Poland: The Press of the Polish Academy of Arts and Sciences. Retrieved 2011-03-17.
{{cite web}}: CS1 maint: date format (link) - "Industry and community - Key dates". United Kingdom Parliament. Retrieved 2011-03-28.
- ^ Frederik Hyttel (May 2009). Working man's pint - An investigation of the implementation of the metric system in Britain 1851-1979 (PDF) (BA thesis). Bath, United Kingdom: Bath Spa University. Retrieved 2011-03-29.
- "Metrication status and history". United States Metrication Association. 2009. Retrieved 2011-05-19.
- 29th Congress of the United States, Session 1 (May 13, 1866). "H.R. 596, An Act to authorize the use of the metric system of weights and measures". Retrieved 2011-05-19.
{{cite web}}: CS1 maint: numeric names: authors list (link) - Barbrow, Louis E.; Judson, Lewis V. (1976). "Use of metric system officially permitted". Weights and Measures Standards of the United States: A brief history. NIST. Retrieved 2011-05-19.
- Barbrow, Louis E.; Judson, Lewis V. (1976). "The Mendenhall Order" (PDF). Weights and Measures Standards of the United States: A brief history. NIST. Retrieved 2011-05-19.
- International Bureau of Weights and Measures (2006), The International System of Units (SI) (PDF) (8th ed.), p. 109, ISBN 92-822-2213-6, archived (PDF) from the original on 2021-06-04, retrieved 2021-12-16
- John Murrell. "A Very Brief History of Thermodynamics" (PDF). Chemistry Department, University of Sussex. Retrieved 2011-03-10.
- Kapil Subramanian (25 February 2011). "How the electric telegraph shaped electromagnetism" (PDF). Current Science. 100 (4). Retrieved 2011-05-12.
- Thomson, William; Joule, James Prescott; Maxwell, James Clerk; Jenkin, Flemming (1873). "First Report – Cambridge 3 October 1862". In Jenkin, Flemming (ed.). Reports on the Committee on Standards of Electrical Resistance - Appointed by the British Association for the Advancement of Science. London. pp. 1–3. Retrieved 2011-05-12.
{{cite book}}: CS1 maint: location missing publisher (link) - Thomson, William; Joule, James Prescott; Maxwell, James Clerk; Jenkin, Flemming (1873). "Second report - Newcastle-upon-Tyne 26 August 1863". In Jenkin, Flemming (ed.). Reports on the Committee on Standards of Electrical Resistance - Appointed by the British Association for the Advancement of Science. London. pp. 39–41. Retrieved 2011-05-12.
{{cite book}}: CS1 maint: location missing publisher (link) - J C Maxwell (1873). A treatise on electricity and magnetism. Vol. 1. Oxford: Clarenden Press. pp. 1–3. Retrieved 2011-05-12.
- ^ J C Maxwell (1873). A treatise on electricity and magnetism. Vol. 2. Oxford: Clarenden Press. pp. 242–245. Retrieved 2011-05-12.
- Professor Everett, ed. (1874). "First Report of the Committee for the Selection and Nomenclature of Dynamical and Electrical Units". Report on the Forty-third Meeting of the British Association for the Advancement of Science held at Bradford in September 1873. British Association for the Advancement of Science: 222–225. Retrieved 2011-05-10.
- "centimeter-gram-second systems of units". Sizes, Inc. 6 August 2001. Retrieved 2011-04-07.
- ^ "The International System of Units". Satellite Today. 1 February 2000. Retrieved 2011-04-05.
- Russ Rowlett (4 December 2008). "How Many? A Dictionary of Units of Measurement: "ab-"". University of North Carolina at Chapel Hill. Retrieved 2011-05-12.
- Russ Rowlett (1 September 2004). "How Many? A Dictionary of Units of Measurement: "stat-"". University of North Carolina at Chapel Hill. Retrieved 2011-05-12.
- Dan Petru Danescu (9 January 2009). "The evolution of the Gaussian Units" (PDF). The general journal of science. Retrieved 2011-05-07.
- "Gaussian, SI and Other Systems of Units in Electromagnetic Theory" (PDF). Physics 221A, Fall 2010, Appendix A. Berkeley: Department of Physics University of California. Retrieved 2011-05-07.
- "A brief history of SI". NIST. Retrieved 2011-03-29.
- ^ "In the beginning... Giovanni Giorgi". International Electrotechnical Commission. 2011. Retrieved 2011-04-05.
- it:Associazione Elettrotecnica Italiana (in Italian)
- Silvanus P. Thompson. "In the beginning...Lord Kelvin". International Electrotechnical Commission. Retrieved 2011-05-10.
- "farad". Sizes, Inc. 9 June 2007. Retrieved 2011-05-10.
-
 This article incorporates text from a publication now in the public domain: "Mètre", Grand dictionnaire universel du XIXe siècle, vol. 17 (Suppl. 2), Paris: Pierre Larousse, 1890, p. 1587.
This article incorporates text from a publication now in the public domain: "Mètre", Grand dictionnaire universel du XIXe siècle, vol. 17 (Suppl. 2), Paris: Pierre Larousse, 1890, p. 1587.
- The term "prototype" does not imply that it was the first in a series and that other standard metres would come after it: the "prototype" metre was the one that came first in the logical chain of comparisons, that is the metre to which all other standards were compared.
- Text of the treaty: "Convention du mètre" (PDF) (in French). Retrieved 2011-03-08.
- Jabbour, Z.J.; Yaniv, S.L. (2001). "The Kilogram and Measurements of Mass and Force" (PDF). J. Res. Natl. Inst. Stand. Technol. 106 (1). National Institute of Standards and Technology (NIST: 25–46. Retrieved 2011-03-28.
- Barrel, H. (1962), "The Metre", Contemp. Phys., 3 (6): 415–34, Bibcode:1962ConPh...3..415B, doi:10.1080/00107516208217499.
- International Bureau of Weights and Measures (2006), The International System of Units (SI) (PDF) (8th ed.), pp. 142–43, 148, ISBN 92-822-2213-6, archived (PDF) from the original on 2021-06-04, retrieved 2021-12-16.
- Phelps, F. M., III (1966), "Airy Points of a Meter Bar", Am. J. Phys., 34 (5): 419–22, Bibcode:1966AmJPh..34..419P, doi:10.1119/1.1973011
{{citation}}: CS1 maint: multiple names: authors list (link). - "Base unit definitions: Meter". NIST. Retrieved 2011-11-15.
- F. J. Smith (1973). "Standard Kilogram Weights - A Story of Precision Fabrication" (PDF). Platinum Metals Review. 17 (2): 66–68.
- G. Girard (1994). "The Third Periodic Verification of National Prototypes of the Kilogram (1988–1992)". Metrologia. 31 (4): 317–336. Bibcode:1994Metro..31..317G. doi:10.1088/0026-1394/31/4/007.
- G.Girard (October 1990). "Le nettoyage-lavage des prototypes du kilogramme au BIPM - The washing and cleaning of kilogram prototypes at the BIPM" (PDF). Bureau International des poids et mesures. Retrieved 2011-04-02.
- ^ "Leap seconds". Time Service Department, U.S. Naval Observatory. Retrieved 2011-04-29.
- F. Richard Stephenson (1982). "Historical Eclipses". Scientific American. 247 (4): 154–163. Bibcode:1982SciAm.247..154S. Retrieved 2011-04-18.
- H.T.Pledge (1959) . "Chapter XXI: Quantum Theory". Science since 1500. Harper Torchbooks. pp. 271–275.
- Thomas W. Leland. G.A. Mansoori (ed.). "Basic Principles of Classical and Statistical Thermodynamics" (PDF). Department of Chemical Engineering, University of Illinois at Chicago. Retrieved 2011-05-10.
- Resolution 3 - Triple point of water; thermodynamic scale with a single fixed point; unit of quantity of heat (joule). 9th Conférence Générale des Poids et Mesures (CGPM). 12–21 October 1948. Retrieved 2011-05-08.
- Resolution 3 - Definition of the thermodynamic temperature scale and. 10th Conférence Générale des Poids et Mesures (CGPM). 5–14 October 1954. Retrieved 2011-05-08.
- Resolution 3 - SI unit of thermodynamic temperature (kelvin) and Resolution 4 - Definition of the SI unit of thermodynamic temperature (kelvin). 9th Conférence Générale des Poids et Mesures (CGPM). 12–21 October 1948. Retrieved 2011-05-08.
- "Techniques for Approximating the International Temperature Scale of 1990" (PDF). Sèvres: BIPM. 1997 . Retrieved 2011-05-10.
- ^ Ian Mills (29 September 2010). "Draft Chapter 2 for SI Brochure, following redefinitions of the base units" (PDF). CCU. Retrieved 2011-01-01.
- Barry N. Taylor (1992). The Metric System: The International System of Units (SI). U. S. Department of Commerce. p. 18. ISBN 0-941375-74-9. (NIST Special Publication 330, 1991 ed.)
- International Bureau of Weights and Measures (2006), The International System of Units (SI) (PDF) (8th ed.), ISBN 92-822-2213-6, archived (PDF) from the original on 2021-06-04, retrieved 2021-12-16
- "Agreement with the CIE". BIPM. Retrieved 2011-05-10.
- "Role of the SUNAMCO Commission". International Union of Pure and Applied Physics. Retrieved 2011-05-10.
- International Bureau of Weights and Measures (2006), The International System of Units (SI) (PDF) (8th ed.), ISBN 92-822-2213-6, archived (PDF) from the original on 2021-06-04, retrieved 2021-12-16
- Resolution 6 - Proposal for establishing a practical system of units of measurement. 9th Conférence Générale des Poids et Mesures (CGPM). 12–21 October 1948. Retrieved 2011-05-08.
- Resolution 7 - Writing and printing of unit symbols and of numbers. 9th Conférence Générale des Poids et Mesures (CGPM). 12–21 October 1948. Retrieved 2011-05-08.
- Resolution 6 - Practical system of units. 10th Conférence Générale des Poids et Mesures (CGPM). 5–14 October 1954. Retrieved 2011-05-08.
- Resolution 12 - Système International d'Unités. 11th Conférence Générale des Poids et Mesures (CGPM). 11–20 October 1960. Retrieved 2011-05-08.
- "Practical realization of the definitions of some important units". SI brochure, Appendix 2. BIPM. 9 September 2010. Retrieved 2011-05-05.
- Ian Mills (29 September 2010). "On the possible future revision of the International System of Units, the SI" (PDF). CCU. Retrieved 2011-01-01.
- "Towards the "new SI"". International Bureau of Weights and Measures (BIPM). Retrieved 2011-02-20.
- "On the possible future revision of the International System of Units, the SI - Draft Resolution A" (PDF). International Committee for Weights and Measures (CIPM). Retrieved 2011-07-14.
- Resolution 1 - On the possible future revision of the International System of Units, the SI (PDF). 24th meeting of the General Conference on Weights and Measures. Sèvres, France. 17 - 21 October 2011. Retrieved 2011-10-25.
{{cite conference}}: Check date values in:|date=(help) - "General Conference on Weights and Measures approves possible changes to the International System of Units, including redefinition of the kilogram" (PDF) (Press release). Sèvres, France: General Conference on Weights and Measures. 23 October 2011. Retrieved 2011-10-25.
Further reading
- Adler, Ken (2002). The Measure of all Things - The Seven-Year-Odyssey that Transformed the World. London: Abacus. ISBN 0 349 11507 9.
{{cite book}}: Check|isbn=value: invalid character (help)
External links
- Naughtin, Pat (2009). "A chronological history of the modern metric system" (PDF). Retrieved 2011-09-15.
{{cite web}}: Cite has empty unknown parameter:|1=(help)
| Systems of measurement | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Current |
| ||||||||||||
| Background |
| ||||||||||||
| Historic |
| ||||||||||||
| Ancient | |||||||||||||
| List articles | |||||||||||||
| Other | |||||||||||||
| Metrication or its opposition by country | |
|---|---|
 . The CGS unit of energy was the "
. The CGS unit of energy was the " and
and  and consequently
and consequently  and
and  were dimensionless.
were dimensionless.







 where
where  (SI units)
(SI units) to unity and potential difference is defined in such a way as to ensure the unit of power calculated by the relation
to unity and potential difference is defined in such a way as to ensure the unit of power calculated by the relation  is identical to the unit of power required to move a mass of one gram a distance of one centimetre in one second when opposed by a force of one dyne. The electromagnetic units of measure were known as the abampere, the abvolt, the abcoulomb and so on.
is identical to the unit of power required to move a mass of one gram a distance of one centimetre in one second when opposed by a force of one dyne. The electromagnetic units of measure were known as the abampere, the abvolt, the abcoulomb and so on. where
where  (SI units)
(SI units) ) to unity and the unit for potential difference were defined to ensure the unit of energy calculated by the relation
) to unity and the unit for potential difference were defined to ensure the unit of energy calculated by the relation  is one erg. The electrostatic units of measure are now known as the statampere, the statvolt, the statcoulomb and so on.
is one erg. The electrostatic units of measure are now known as the statampere, the statvolt, the statcoulomb and so on.
 while resistance had the same dimensions as velocity in the EMU system of units, but had the dimensions of the inverse of velocity in the ESU system of units.
while resistance had the same dimensions as velocity in the EMU system of units, but had the dimensions of the inverse of velocity in the ESU system of units.