| Revision as of 14:41, 3 June 2013 view sourceDVdm (talk | contribs)Autopatrolled, Extended confirmed users, New page reviewers, Pending changes reviewers, Rollbackers138,476 edits →A trivial refutation of one of Dingle's Fumbles (Ref: Talk:Herbert Dingle Archive): Darkened math colour to DarkGreen← Previous edit |
Revision as of 15:17, 3 June 2013 view source DVdm (talk | contribs)Autopatrolled, Extended confirmed users, New page reviewers, Pending changes reviewers, Rollbackers138,476 editsm →A trivial refutation of one of Dingle's Fumbles (Ref: Talk:Herbert Dingle Archive): ForestGreen (and corrected a few typos)Next edit → |
| Line 10: |
Line 10: |
|
: (start quote) |
|
: (start quote) |
|
<div style="padding: 1em; border: solid 3px {{{bordercolor|#a08040}}}; background-color: {{{color|#fff7f7}}};"> |
|
<div style="padding: 1em; border: solid 3px {{{bordercolor|#a08040}}}; background-color: {{{color|#fff7f7}}};"> |
|
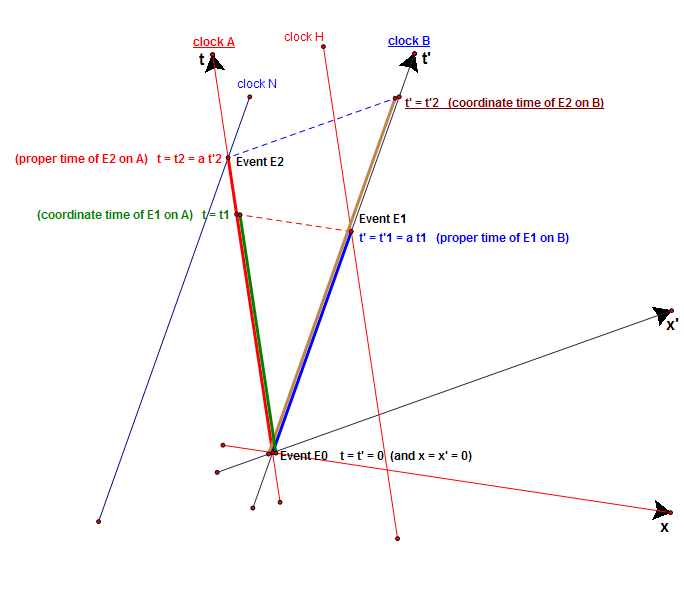
:: {{!xt|Thus, between events E0 and E1, A advances by <math>\color{DarkGreen}{t_1}</math> and B by <math>\color{Blue}{t'_1 = a t_1}</math> by (1). Therefore}} |
|
:: {{!xt|Thus, between events E0 and E1, A advances by <math>\color{ForestGreen}{t_1}</math> and B by <math>\color{Blue}{t'_1 = a t_1}</math> by (1). Therefore}} |
|
::: <math>\frac{\color{DarkGreen}{\text{rate of A}}}{\color{Blue}{\text{rate of B}}} = \frac{\color{DarkGreen}{t_1}}{\color{Blue}{a t_1}} = \frac{1}{a} > 1 \qquad \text{(3)}</math> |
|
::: <math>\frac{\color{ForestGreen}{\text{rate of A}}}{\color{Blue}{\text{rate of B}}} = \frac{\color{ForestGreen}{t_1}}{\color{Blue}{a t_1}} = \frac{1}{a} > 1 \qquad \text{(3)}</math> |
|
:: ... |
|
:: ... |
|
:: {{!xt|Thus, between events E0 and E2, B advances by <math>\color{Brown}{t'_2}</math> and A by <math>\color{Red}{t_2 = a t'_2}</math> by (2). Therefore}} |
|
:: {{!xt|Thus, between events E0 and E2, B advances by <math>\color{Brown}{t'_2}</math> and A by <math>\color{Red}{t_2 = a t'_2}</math> by (2). Therefore}} |
| Line 21: |
Line 21: |
|
: (start correction) |
|
: (start correction) |
|
<div style="padding: 1em; border: solid 3px {{{bordercolor|#a08040}}}; background-color: {{{color|#f7fff7}}};"> |
|
<div style="padding: 1em; border: solid 3px {{{bordercolor|#a08040}}}; background-color: {{{color|#f7fff7}}};"> |
|
:: {{xt|Thus, between events E0 and E1, A, which is '''not present''' at both events, advances by <math>\color{DarkGreen}{t_1}</math> and B, which is '''present''' at both events, by <math>\color{Blue}{t'_1 = a t_1}</math> by (1). Therefore}} |
|
:: {{xt|Thus, between events E0 and E1, A, which is '''not present''' at both events, advances by <math>\color{ForestGreen}{t_1}</math> and B, which is '''present''' at both events, by <math>\color{Blue}{t'_1 = a t_1}</math> by (1). Therefore}} |
|
::: <math>\frac{\color{DirkGreen}{\text{rate of clock not present at both events E0 and E1}}}{\color{Blue}{\text{rate of clock present at both events E0 and E1}}} = \frac{\color{<<DarkGreen}{\text{coordinate time of E1}}}{\color{Blue}{\text{proper time of E1}}} = \frac{\color{DarkGreen}{\text{rate of A}}}{\color{Blue}{\text{rate of B}}} = \frac{\color{DirkGreen}{t_1}}{\color{Blue}{t'_1}} = \frac{\color{DarkGreen}{t_1}}{\color{Blue}{a t_1}} = \frac{1}{a} > 1 \qquad \text{(3)}</math> |
|
::: <math>\frac{\color{ForestGreen}{\text{rate of clock not present at both events E0 and E1}}}{\color{Blue}{\text{rate of clock present at both events E0 and E1}}} = \frac{\color{ForestGreen}{\text{coordinate time of E1}}}{\color{Blue}{\text{proper time of E1}}} = \frac{\color{ForestGreen}{\text{rate of A}}}{\color{Blue}{\text{rate of B}}} = \frac{\color{ForestGreen}{t_1}}{\color{Blue}{t'_1}} = \frac{\color{ForestGreen}{t_1}}{\color{Blue}{a t_1}} = \frac{1}{a} > 1 \qquad \text{(3)}</math> |
|
:: ... |
|
:: ... |
|
:: {{xt|Thus, between events E0 and E2, B, which is '''not present''' at both events, advances by <math>\color{Brown}{t'_2}</math> and A, which is '''present''' at both events, by <math>\color{Red}{t_2 = a t'_2}</math> by (2). Therefore}} |
|
:: {{xt|Thus, between events E0 and E2, B, which is '''not present''' at both events, advances by <math>\color{Brown}{t'_2}</math> and A, which is '''present''' at both events, by <math>\color{Red}{t_2 = a t'_2}</math> by (2). Therefore}} |
 and B by
and B by  by (1). Therefore
by (1). Therefore

 and A by
and A by  by (2). Therefore
by (2). Therefore


