Misplaced Pages

This is an old revision of this page, as edited by Sox2225 (talk | contribs) at 17:39, 12 September 2013. The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.

I the fourth grade, I was riding the bus on my way to my elementary school, when I shit my pants. Thank god I was wearing whitey tighties that day because they acted as a diaper to keep my feces contained. I remember all the kids laughing, throwing items such as sharp pencils, and most of all, vomiting from the intense odor that just was released from my butthole. I will never forget that day.

Since then I have gone on to be a successful faggot. I graduated from University of Douche in Ohio. I couldn't of done this with out the love and support of all my pet lobsters. They have always known how I was feeling in my lowest lows. I'd also like to thank my sister. I know that we had some sexual encounters with our father and with each other growing up. But I think those experiences help made me the "man" I am today. There's not a girl in world I would have rather lost my viginity to, love you sister.

I think this is enough fucking around now. I don't care if you stop me from making edits. I can create a new profile and continue to write what I feel like on these pages.

Thank you I'm sorry about your sister and the incident you had in the bus in the fourth grade.

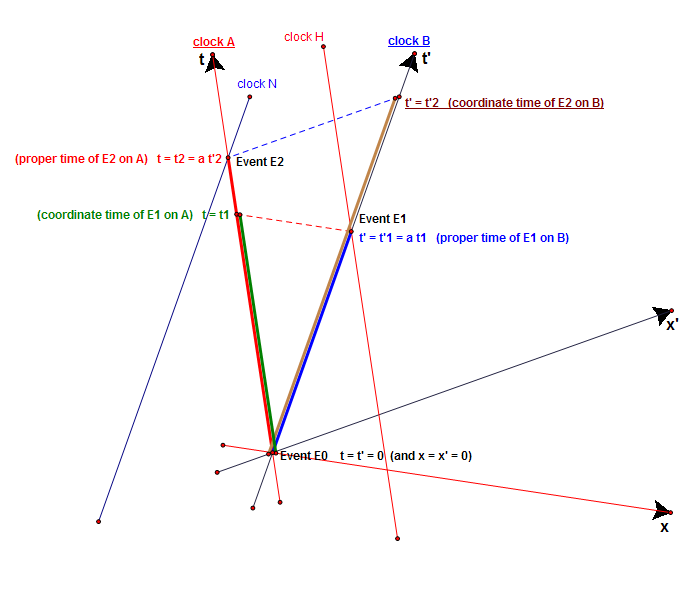
A trivial refutation of one of Dingle's Fumbles (Ref: Talk:Herbert Dingle Archive)

On page 230 in this appendix to "Science At the Crossroads", Dingle writes:

(start quote)

Thus, between events E0 and E1, A advances by ${\displaystyle \color {ForestGreen}{t_{1}}}$ and B by ${\displaystyle \color {Blue}{t'_{1}=at_{1}}}$ by (1). Therefore

${\displaystyle {\frac {\color {ForestGreen}{\text{rate of A}}}{\color {Blue}{\text{rate of B}}}}={\frac {\color {ForestGreen}{t_{1}}}{\color {Blue}{at_{1}}}}={\frac {1}{a}}>1\qquad {\text{(3)}}}$

...

Thus, between events E0 and E2, B advances by ${\displaystyle \color {Brown}{t'_{2}}}$ and A by ${\displaystyle \color {Red}{t_{2}=at'_{2}}}$ by (2). Therefore

${\displaystyle {\frac {\color {Red}{\text{rate of A}}}{\color {Brown}{\text{rate of B}}}}={\frac {\color {Red}{at'_{2}}}{\color {Brown}{t'_{2}}}}=a<1\qquad {\text{(4)}}}$

Equations (3) and (4) are contradictory: hence the theory requiring them must be false.

(end quote)

Dingle should have written as follows:

(start correction)

Thus, between events E0 and E1, A, which is not present at both events, advances by ${\displaystyle \color {ForestGreen}{t_{1}}}$ and B, which is present at both events, by ${\displaystyle \color {Blue}{t'_{1}=at_{1}}}$ by (1). Therefore

${\displaystyle {\frac {\color {ForestGreen}{\text{rate of clock not present at both events E0 and E1}}}{\color {Blue}{\text{rate of clock present at both events E0 and E1}}}}={\frac {\color {ForestGreen}{\text{coordinate time of E1}}}{\color {Blue}{\text{proper time of E1}}}}={\frac {\color {ForestGreen}{\text{rate of A}}}{\color {Blue}{\text{rate of B}}}}={\frac {\color {ForestGreen}{t_{1}}}{\color {Blue}{t'_{1}}}}={\frac {\color {ForestGreen}{t_{1}}}{\color {Blue}{at_{1}}}}={\frac {1}{a}}>1\qquad {\text{(3)}}}$

...

Thus, between events E0 and E2, B, which is not present at both events, advances by ${\displaystyle \color {Brown}{t'_{2}}}$ and A, which is present at both events, by ${\displaystyle \color {Red}{t_{2}=at'_{2}}}$ by (2). Therefore

${\displaystyle {\frac {\color {Brown}{\text{rate of clock not present at both events E0 and E2}}}{\color {Red}{\text{rate of clock present at both events E0 and E2}}}}={\frac {\color {Brown}{\text{coordinate time of E2}}}{\color {Red}{\text{proper time of E2}}}}={\frac {\color {Brown}{\text{rate of B}}}{\color {Red}{\text{rate of A}}}}={\frac {\color {Brown}{t'_{2}}}{\color {Red}{t_{2}}}}={\frac {\color {Brown}{t'_{2}}}{\color {Red}{at'_{2}}}}={\frac {1}{a}}>1\qquad {\text{(4)}}}$

Equations (3) and (4) are consistent and say that any event's coordinate time is always larger than its proper time:

hence there is no reason to say that the theory requiring them must be false.

(end correction)

DVdm 12:18, 6 August 2007 (UTC)