This is an old revision of this page, as edited by 166.199.8.61 (talk) at 12:42, 24 November 2023 (2 col ref layout). The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.
Revision as of 12:42, 24 November 2023 by 166.199.8.61 (talk) (2 col ref layout)(diff) ← Previous revision | Latest revision (diff) | Newer revision → (diff) Particular case of the generalized extreme value distribution
Probability density function | |||
Cumulative distribution function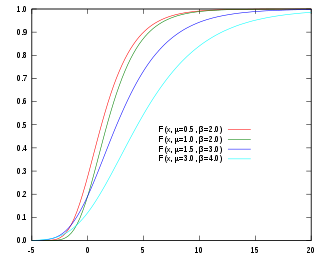 | |||
| Notation | |||
|---|---|---|---|
| Parameters |
location (real) scale (real) | ||
| Support | |||
|
where | |||
| CDF | |||
| Mean |
where is the Euler–Mascheroni constant | ||
| Median | |||
| Mode | |||
| Variance | |||
| Skewness | |||
| Excess kurtosis | |||
| Entropy | |||
| MGF | |||
| CF | |||
In probability theory and statistics, the Gumbel distribution (also known as the type-I generalized extreme value distribution) is used to model the distribution of the maximum (or the minimum) of a number of samples of various distributions.
This distribution might be used to represent the distribution of the maximum level of a river in a particular year if there was a list of maximum values for the past ten years. It is useful in predicting the chance that an extreme earthquake, flood or other natural disaster will occur. The potential applicability of the Gumbel distribution to represent the distribution of maxima relates to extreme value theory, which indicates that it is likely to be useful if the distribution of the underlying sample data is of the normal or exponential type. This article uses the Gumbel distribution to model the distribution of the maximum value. To model the minimum value, use the negative of the original values.
The Gumbel distribution is a particular case of the generalized extreme value distribution (also known as the Fisher–Tippett distribution). It is also known as the log-Weibull distribution and the double exponential distribution (a term that is alternatively sometimes used to refer to the Laplace distribution). It is related to the Gompertz distribution: when its density is first reflected about the origin and then restricted to the positive half line, a Gompertz function is obtained.
In the latent variable formulation of the multinomial logit model — common in discrete choice theory — the errors of the latent variables follow a Gumbel distribution. This is useful because the difference of two Gumbel-distributed random variables has a logistic distribution.
The Gumbel distribution is named after Emil Julius Gumbel (1891–1966), based on his original papers describing the distribution.
Definitions
The cumulative distribution function of the Gumbel distribution is
Standard Gumbel distribution
The standard Gumbel distribution is the case where and with cumulative distribution function
and probability density function
In this case the mode is 0, the median is , the mean is (the Euler–Mascheroni constant), and the standard deviation is
The cumulants, for n > 1, are given by
Properties
The mode is μ, while the median is and the mean is given by
- ,
where is the Euler–Mascheroni constant.
The standard deviation is hence
At the mode, where , the value of becomes , irrespective of the value of
If are iid Gumbel random variables with parameters then is also a Gumbel random variable with parameters .
If are iid random variables such that has the same distribution as for all natural numbers , then is necessarily Gumbel distributed with scale parameter (actually it suffices to consider just two distinct values of k>1 which are coprime).
Related distributions
- If X has a Gumbel distribution, then the conditional distribution of Y = −X given that Y is positive, or equivalently given that X is negative, has a Gompertz distribution. The c.d.f. G of Y is related to F, the c.d.f. of X, by the formula for y > 0 . Consequently, the densities are related by The Gompertz density is proportional to a reflected Gumbel density, restricted to the positive half-line.
- If X is an exponentially distributed variable with mean 1, then −log(X) has a standard Gumbel distribution.
- If and are independent, then (see Logistic distribution).
- If are independent, then Note that More generally, the distribution of linear combinations of independent Gumbel random variables can be approximated by GNIG and GIG distributions.
- Theory related to the generalized multivariate log-gamma distribution provides a multivariate version of the Gumbel distribution.
Occurrence and applications

Gumbel has shown that the maximum value (or last order statistic) in a sample of random variables following an exponential distribution minus the natural logarithm of the sample size approaches the Gumbel distribution as the sample size increases.
Concretely, let be the probability distribution of and its cumulative distribution. Then the maximum value out of realizations of is smaller than if and only if all realizations are smaller than So the cumulative distribution of the maximum value satisfies
and, for large the right-hand-side converges to
In hydrology, therefore, the Gumbel distribution is used to analyze such variables as monthly and annual maximum values of daily rainfall and river discharge volumes, and also to describe droughts.
Gumbel has also shown that the estimator r/ n + 1 for the probability of an event – where r is the rank number of the observed value in the data series and n is the total number of observations – is an unbiased estimator of the cumulative probability around the mode of the distribution. Therefore, this estimator is often used as a plotting position.
In number theory, the Gumbel distribution approximates the number of terms in a random partition of an integer as well as the trend-adjusted sizes of maximal prime gaps and maximal gaps between prime constellations.
Gumbel reparametrization tricks
In machine learning, the Gumbel distribution is sometimes employed to generate samples from the categorical distribution. This technique is called "Gumbel-max trick" and is a special example of a "reparametrization trick".
In detail, let be nonnegative, and not all zero, and let be independent samples of Gumbel(0, 1), then by routine integration, That is,
Equivalently, given any we can sample from its Boltzmann distribution by
Related equations include:
- If then
- that is, the Gumbel distribution is a max-stable distribution family.
Random variate generation
Further information: Non-uniform random variate generationSince the quantile function (inverse cumulative distribution function), , of a Gumbel distribution is given by
the variate has a Gumbel distribution with parameters and when the random variate is drawn from the uniform distribution on the interval .
Probability paper

In pre-software times probability paper was used to picture the Gumbel distribution (see illustration). The paper is based on linearization of the cumulative distribution function :
In the paper the horizontal axis is constructed at a double log scale. The vertical axis is linear. By plotting on the horizontal axis of the paper and the -variable on the vertical axis, the distribution is represented by a straight line with a slope 1. When distribution fitting software like CumFreq became available, the task of plotting the distribution was made easier.
See also
- Type-2 Gumbel distribution
- Extreme value theory
- Generalized extreme value distribution
- Fisher–Tippett–Gnedenko theorem
- Emil Julius Gumbel
References
- Gumbel, E.J. (1935), "Les valeurs extrêmes des distributions statistiques" (PDF), Annales de l'Institut Henri Poincaré, 5 (2): 115–158
- Gumbel E.J. (1941). "The return period of flood flows". The Annals of Mathematical Statistics, 12, 163–190.
- ^ Oosterbaan, R.J. (1994). "Frequency and regression analysis" (PDF). In Ritzema, H.P. (ed.). Drainage Principles and Applications. ILRI Publications. Vol. 16. Wageningen, NL: International Institute for Land Reclamation and Improvement (ILRI). Chapter 6, pages 175–224. ISBN 90-70754-33-9.
- Willemse, W.J.; Kaas, R. (2007). "Rational reconstruction of frailty-based mortality models by a generalisation of Gompertz' law of mortality" (PDF). Insurance: Mathematics and Economics. 40 (3): 468. doi:10.1016/j.insmatheco.2006.07.003.
- Marques, F.; Coelho, C.; de Carvalho, M. (2015). "On the distribution of linear combinations of independent Gumbel random variables" (PDF). Statistics and Computing. 25 (3): 683‒701. doi:10.1007/s11222-014-9453-5. S2CID 255067312.
- "CumFreq" – via waterlog.info.
software for probability distribution fitting
- "Gumbel distribution and exponential distribution". 29 January 2020 – via math.stackexchange.com.
{{cite web}}: Unknown parameter|authors=ignored (help) - Gumbel, E.J. (1954). Statistical Theory of Extreme Values and Some Practical Applications. Applied Mathematics Series. Vol. 33 (1st ed.). U.S. Department of Commerce, National Bureau of Standards. ASIN B0007DSHG4.
- Burke, Eleanor J.; Perry, Richard H.J.; Brown, Simon J. (2010). "An extreme value analysis of UK drought and projections of change in the future". Journal of Hydrology. 388 (1–2): 131–143. Bibcode:2010JHyd..388..131B. doi:10.1016/j.jhydrol.2010.04.035.
- Erdös, Paul; Lehner, Joseph (1941). "The distribution of the number of summands in the partitions of a positive integer". Duke Mathematical Journal. 8 (2): 335. doi:10.1215/S0012-7094-41-00826-8.
- Kourbatov, A. (2013) . "Maximal gaps between prime k-tuples: A statistical approach". Journal of Integer Sequences. 16. Article 13.5.2. arXiv:1301.2242. Bibcode:2013arXiv1301.2242K. doi:10.48550/arXiv.1301.2242.
- Jang, Eric; Gu, Shixiang; Poole, Ben (April 2017). Categorical Reparametrization with Gumble-Softmax. 2017 International Conference on Learning Representations (ICLR).
- Balog, Matej; Tripuraneni, Nilesh; Ghahramani, Zoubin; Weller, Adrian (2017-07-17). "Lost Relatives of the Gumbel Trick". International Conference on Machine Learning. PMLR: 371–379. arXiv:1706.04161.








 is the
is the 








 and
and  with cumulative distribution function
with cumulative distribution function


 , the mean is
, the mean is  (the
(the 

 and the mean is given by
and the mean is given by
 ,
, is
is  hence
hence 
 , the value of
, the value of  becomes
becomes  , irrespective of the value of
, irrespective of the value of 
 are iid Gumbel random variables with parameters
are iid Gumbel random variables with parameters  then
then  is also a Gumbel random variable with parameters
is also a Gumbel random variable with parameters  .
.
 are iid random variables such that
are iid random variables such that  has the same distribution as
has the same distribution as  for all natural numbers
for all natural numbers  , then
, then  (actually it suffices to consider just two distinct values of k>1 which are coprime).
(actually it suffices to consider just two distinct values of k>1 which are coprime).
 for y > 0 . Consequently, the densities are related by
for y > 0 . Consequently, the densities are related by  The
The  and
and  are independent, then
are independent, then  (see
(see  are independent, then
are independent, then  Note that
Note that  More generally, the distribution of linear combinations of independent Gumbel random variables can be approximated by GNIG and GIG distributions.
More generally, the distribution of linear combinations of independent Gumbel random variables can be approximated by GNIG and GIG distributions. be the probability distribution of
be the probability distribution of  and
and  its cumulative distribution. Then the maximum value out of
its cumulative distribution. Then the maximum value out of  realizations of
realizations of  is smaller than
is smaller than  if and only if all
if and only if all  So the cumulative distribution of the maximum value
So the cumulative distribution of the maximum value 
 the right-hand-side converges to
the right-hand-side converges to 
 be nonnegative, and not all zero, and let
be nonnegative, and not all zero, and let  be independent samples of Gumbel(0, 1), then by routine integration,
be independent samples of Gumbel(0, 1), then by routine integration, That is,
That is, 
 we can sample from its
we can sample from its 
 then
then 

 that is, the Gumbel distribution is a max-stable distribution family.
that is, the Gumbel distribution is a max-stable distribution family.
 , of a Gumbel distribution is given by
, of a Gumbel distribution is given by

 has a Gumbel distribution with parameters
has a Gumbel distribution with parameters  is drawn from the
is drawn from the  .
.
 :
:

 -variable on the vertical axis, the distribution is represented by a straight line with a slope 1
-variable on the vertical axis, the distribution is represented by a straight line with a slope 1 . When
. When