This is an old revision of this page, as edited by Headbomb (talk | contribs) at 19:26, 19 July 2008 (minor cleanup using AWB). The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.
Revision as of 19:26, 19 July 2008 by Headbomb (talk | contribs) (minor cleanup using AWB)(diff) ← Previous revision | Latest revision (diff) | Newer revision → (diff)- For the relation of the AdS/CFT correspondence to the general context of string theory, see String theory.
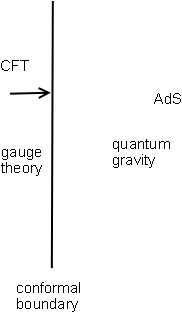
In physics, the AdS/CFT correspondence (anti-de-Sitter space/conformal field theory correspondence), sometimes called the Maldacena duality, is the conjectured equivalence between a string theory defined on one space, and a quantum field theory without gravity defined on the conformal boundary of this space, whose dimension is lower by one or more. The name suggests that the first space is the product of anti de Sitter space (AdS) with some closed manifold like sphere, orbifold, or noncommutative space, and that the quantum field theory is a conformal field theory (CFT).
An example is the duality between Type IIB string theory on AdS5 × S space (a product of five dimensional AdS space with a five dimensional sphere) and a supersymmetric N=4 Yang-Mills gauge theory (which is a conformal field theory) on the 4-dimensional boundary of AdS5. It is the most successful realization of the holographic principle, a speculative idea about quantum gravity originally proposed by Gerard 't Hooft and improved and promoted by Leonard Susskind.
The AdS/CFT correspondence was originally proposed by Juan Maldacena in late 1997. Important aspects of the correspondence were given in articles by Gubser, Klebanov and Polyakov and by Edward Witten. The correspondence has also been generalized to many other (non-AdS) backgrounds and their dual (non-conformal) theories. In about five years, Maldacena's article had 3000 citations and became one of the most important conceptual breakthroughs in theoretical physics of the 1990s, providing stark new insight into both quantum gravity and QCD.
The AdS/CFT correspondence should not be confused with algebraic holography or "Rehren duality"; although these are sometimes identified with AdS/CFT, string theorists agree that they are different things.
Conformal boundary
It is possible to make a Weyl transformation on AdS so that it now has a boundary. If we do that, it turns out that its boundary is a conformal field theory in one lower dimension.
To make things more concrete, let's choose a particular coordinatization, the half-space coordinatization:
After a Weyl transformation , we get
which has the Minkowski metric as the boundary at . This is called the conformal boundary.
Source fields
Basically, the correspondence runs as follows; if we deform the CFT by certain source fields by adding the source , this will be dual to an AdS theory with a bulk field J with the boundary condition
where Δ is the conformal dimension of the local operator and k is the number of covariant indices of minus the number of contravariant indices. Only gauge-invariant operators are allowed.
Here, we have a dual source field for every gauge-invariant local operator we have.
Using generating functionals, the relation is expressed as
The left hand side is the vacuum expectation value of the time-ordered exponential of the operators over the conformal field theory. The right hand side is the quantum gravity generating functional with the given conformal boundary condition. The right hand side is evaluated by finding the classical solutions to the effective action subject to the given boundary conditions.
Some examples
The stress-energy operator on the CFT side is dual to the transverse components of the metric on the AdS side. Since the stress-energy operator has a conformal weight of 4, the AdS metric ought to go as , which is true for AdS. Also, the graviton has to be massless, just as it should.
If there is a global internal symmetry G on the CFT side, its Noether current J will be dual to the transverse components of a gauge connection for a Yang-Mills gauge theory with G as the gauge group on the AdS side. Since J has a conformal weight of 3, the dual Yang-Mills gauge boson ought to have zero bulk mass, just as it should.
A scalar operator with conformal weight Δ will be dual to a scalar bulk field with a bulk mass of .
Particles
A CFT bound state of size r is dual to a bulk particle approximately localized at z=r.
Supersymmetry
We need to match up conformal supersymmetry in 4D with AdS supersymmetry in 5D. The symmetry supergroups in both cases happen to match up, as they should. There are real SUSY generators and the bosonic part consists of the conformal cum AdS group Spin(4,2) times an internal group . See superconformal algebra for more details.
For the case , we have 32 real SUSY generators and an internal group . Now, and Spin(6) is the isometry group of S with spinorial fields. The bosonic spatial isometry group of is .
In 10D SUSY, we have 32 real SUSY generators. In a generic curved spacetime, some of the SUSY generators will be broken but in the special compactification of with both factors having the same radius, we are left 32 real unbroken generators. However, the bosonic spatial isometries with 55 generators in the flat case is now broken to with 30 generators. also has a symmetry and this is identified with .
The source of the curvature lies in the nonzero value of a self-dual 5-form flux belonging to the SUGRA multiplet. The integral of this 5-flux over S has to be a nonzero integer (if it's zero, we have no stress-energy tensor). Because the part of the 5-flux lying in AdS5 contains a time component, it gives rise to negative curvature. The part of the 5-flux lying in S doesn't have a time component, and so, it gives rise to a positive curvature.
The SUGRA multiplet also contains a dilaton and axion field. They correspond to the gauge field coupling and theta angle of the dual superYang-Mills theory.
There are real SUSY generators with as the obligatory R-symmetry.
11D supergravity contains 32 real SUSY generators. There is a particular compactification, , the Freund-Rubin compactification, which preserves all 32 real generators. The bosonic isometry group is reduced to . After a Kaluza-Klein decomposition over S, we get SUSY. A 7-form magnetic flux is present over S. Its integral over S has to be integral and nonzero.
See also
External links
- Maldacena, The Large N Limit of Superconformal Field Theories and Supergravity, arXiv:hep-th/9711200.
- Witten, Anti-de Sitter Space and Holography, arXiv:hep-th/9802150.
- Gubser, Klebanov and Polyakov, Gauge Theory Correlators from Non-Critical String Theory, arXiv:hep-th/9802109.
- Aharony et al, Large N Field Theories, String Theory and Gravity, arXiv:hep-th/9905111. (261 pages of introductory text and review.)
- AdS/CFT correspondence on arxiv.org.
- The Illusion of Gravity - Juan Maldacena, Scientific American.
- University of Michigan Lecture
- Professor Hirosi Ooguri's notes
- Meeting on the subject
- Database of articles; Supersymmetric Gauge Theories and the AdS/CFT Correspondence
- Shadow World. The state of the AdS/CFT conjecture on its 10th anniversary. Science News magazine, November 17, 2007

 , we get
, we get

 . This is called the
. This is called the
 , this will be dual to an AdS theory with a bulk field J with the boundary condition
, this will be dual to an AdS theory with a bulk field J with the boundary condition

 and k is the number of covariant indices of
and k is the number of covariant indices of 
 examples
examples , which is true for AdS. Also, the graviton has to be massless, just as it should.
, which is true for AdS. Also, the graviton has to be massless, just as it should.
 .
.
 real SUSY generators and the bosonic part consists of the conformal cum AdS group Spin(4,2) times an internal group
real SUSY generators and the bosonic part consists of the conformal cum AdS group Spin(4,2) times an internal group  . See
. See  , we have 32 real SUSY generators and an internal group
, we have 32 real SUSY generators and an internal group  . Now,
. Now,  and Spin(6) is the
and Spin(6) is the  is
is  .
.
 10D SUSY, we have 32 real SUSY generators. In a generic curved spacetime, some of the SUSY generators will be broken but in the special compactification of
10D SUSY, we have 32 real SUSY generators. In a generic curved spacetime, some of the SUSY generators will be broken but in the special compactification of  symmetry and this is identified with
symmetry and this is identified with  .
.

 real SUSY generators with
real SUSY generators with  as the obligatory R-symmetry.
as the obligatory R-symmetry.

 , the
, the  . After a
. After a  SUSY. A 7-form magnetic flux is present over S. Its integral over S has to be integral and nonzero.
SUSY. A 7-form magnetic flux is present over S. Its integral over S has to be integral and nonzero.