This is an old revision of this page, as edited by OpenScience709 (talk | contribs) at 22:01, 6 September 2021 (Rewrote the entire article since it is severely lacking. Expanded on the connection between the three generation functionals as well as introduced new sections on additional information concerning the effective action.). The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.
Revision as of 22:01, 6 September 2021 by OpenScience709 (talk | contribs) (Rewrote the entire article since it is severely lacking. Expanded on the connection between the three generation functionals as well as introduced new sections on additional information concerning the effective action.)(diff) ← Previous revision | Latest revision (diff) | Newer revision → (diff) In quantum field theory, a quantum corrected version of the classical actionIn quantum field theory, the quantum effective action is a modified expression for the classical action taking into account quantum corrections while ensuring that the principle of least action applies, meaning that extremizing the effective action yields the equations of motion for the vacuum expectation values of the quantum fields. The effective action also acts as a generating functional for one-particle irreducible correlation functions. The potential component of the effective action is called the effective potential, with the expectation value of the true vacuum being the minimum of this potential rather than the classical potential, making it important for studying spontaneous symmetry breaking.
It was first defined perturbatively by Jeffrey Goldstone and Steven Weinberg in 1962, while the non-perturbative definition was introduced by Bryce DeWitt in 1963 and independently by Giovanni Jona-Lasinio in 1964.
Generating Functionals
These generation functionals also have applications in statistical mechanics and information theory, with slightly different factors of and sign conventions.
A quantum field theory with action can be fully described in the path integral formalism using the partition functional
Since it corresponds to vacuum-to-vacuum transitions in the presence of a classical external current , it can be evaluated perturbatively as the sum of all connected and disconnected Feynman diagrams. It is also the generating functional for correlation functions
One can define another useful generating functional responsible for generating connected correlation functions
which is calculated perturbatively as the sum of all connected diagrams. Here connected is interpreted in the sense of the cluster decomposition theorem, meaning that the correlation functions approach zero at large spacelike separations. General correlation functions can always be written as a sum of products of connected correlation functions.
The quantum effective action is defined using the Legendre transformation of
where is the current for which the scalar field has the expectation value , hence is defined implicitly as the solution to
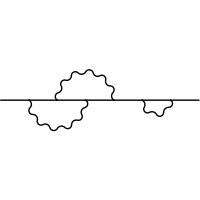 Example of a diagram that is not one-particle irreducible.
Example of a diagram that is not one-particle irreducible. Example of a diagram that is one-particle irreducible.
Example of a diagram that is one-particle irreducible.
The hat notation is used to distinguish between the scalar field operator and some particular expectation value of that operator , which depends on the state under consideration. Taking the functional derivative of the Legendre transformation with respect to yields
In the absence of an external current , the above shows that the vacuum expectation value of the fields extremize the quantum effective action rather than the classical action. This is nothing more than the principle of least action in the full quantum field theory. The reason for why the quantum theory requires this modification comes from the path integral perspective since all possible field configurations contribute to the path integral, while in classical field theory only the classical configurations contribute.
The effective action is also the generation functional for one-particle irreducible (1PI) correlation functions. 1PI diagrams are connected graphs that cannot be disconnected into two pieces by cutting a single internal line. Therefore we have
with being the sum of all 1PI Feynman diagrams. The close connection between and means that there are a number of very useful relations between their correlation functions. For example, the two-point correlation function, which is nothing less than the propagator, is the inverse of the 1PI two-point correlation function
Methods for calculating the effective action
A direct way to calculate the effective action perturbatively as a sum of 1PI diagrams is to sum over all 1PI vacuum diagrams acquired using the Feynman rules derived from the shifted action . This works because any place where appears in any of the propagators or vertices is a place where an external line could be attached.
Alternatively, the approximation to the action can be found by considering the expansion of the partition function around the classical vacuum expectation value field configuration , yielding the one-loop approximation
Symmetries
Symmetries of the classical action are not automatically symmetries of the quantum effective action . If the classical action has a continuous symmetry depending on some functional
then this directly imposes the constraint
This identity is an example of a Slavnov-Taylor identity. It is identical to the requirement that the effective action is invariant under the symmetry transformation
This symmetry is identical to the original symmetry for the important class of linear symmetries
For non-linear functionals the two symmetries generally differ because the average of a non-linear functional is not equivalent to the functional of an average.
Convexity

The effective potential at always gives the minimum of the expectation value of the energy density for the set of states satisfying . This definition over a large set of states is necessary because multiple different states may result in the same expectation value. It can further be shown that the effective potential is necessarily a convex function .
Calculating the effective potential perturbatively can sometimes yield a non-convex result, such as a potential that has two local minima. However, the true effective potential is still convex, becoming approximately linear where the apparent effective potential fails to be convex. The contradiction occurs when one is dealing with a situation in which the vacuum is unstable, while perturbation theory necessarily assumes that the vacuum is stable. For example, consider an apparent effective potential with two local minima whose expectation values and are the expectation values for the states and , respectively. Then any in the non-convex region of can also be acquired for some using
However, the energy density of this state is meaning cannot be the correct effective potential at since it did not minimize the energy density. Rather the true effective potential is equal to or lower than this linear construction, which restores convexity.
References
- Weinberg, Steven; Goldstone, Jeffrey (August 1962). "Broken Symmetries". Phys. Rev. 127 (3): 965–970. doi:10.1103/PhysRev.127.965. Retrieved 2021-09-06.
- DeWitt, B.; DeWitt, C. (1987). Relativité, groupes et topologie = Relativity, groups and topology : lectures delivered at Les Houches during the 1963 session of the Summer School of Theoretical Physics, University of Grenoble. Gordon and Breach. ISBN 0677100809.
- Jona-Lasinio, Giovanni (31 August 1964). "Relativistic Field Theories with Symmetry-Breaking Solutions". Il Nuovo Cimento. 34 (6): 1790–1795. doi:10.1007/BF02750573. Retrieved 2021-09-06.
- Kleinert, Hagen (2016). "22" (PDF). Particles and Quantum Fields. World Scientific Publishing. p. 1257. ISBN 9789814740920.
- Weinberg, Steven (1995). "16". The Quantum Theory of Fields Volume 2. Vol. 2. Cambridge University Press. p. 72-74. ISBN 9780521670548.
Further Reading
- M.D. Schwartz: Quantum Field Theory and the Standard Model, Cambridge University Press 2014
- D.J. Toms: The Schwinger Action Principle and Effective Action, Cambridge University Press 2007
- S. Weinberg: The Quantum Theory of Fields, Vol.II, Cambridge University Press 1996
 and sign conventions.
and sign conventions.
 can be fully described in the
can be fully described in the 
 , it can be evaluated perturbatively as the sum of all connected and disconnected
, it can be evaluated perturbatively as the sum of all connected and disconnected 
 responsible for generating connected correlation functions
responsible for generating connected correlation functions



 is the current for which the scalar field has the expectation value
is the current for which the scalar field has the expectation value  , hence is defined implicitly as the solution to
, hence is defined implicitly as the solution to

 and some particular expectation value of that operator
and some particular expectation value of that operator 
 , the above shows that the vacuum expectation value of the fields extremize the quantum effective action rather than the classical action. This is nothing more than the principle of least action in the full quantum field theory. The reason for why the quantum theory requires this modification comes from the path integral perspective since all possible field configurations contribute to the path integral, while in classical field theory only the classical configurations contribute.
, the above shows that the vacuum expectation value of the fields extremize the quantum effective action rather than the classical action. This is nothing more than the principle of least action in the full quantum field theory. The reason for why the quantum theory requires this modification comes from the path integral perspective since all possible field configurations contribute to the path integral, while in classical field theory only the classical configurations contribute.

 being the sum of all 1PI Feynman diagrams. The close connection between
being the sum of all 1PI Feynman diagrams. The close connection between 
 perturbatively as a sum of 1PI diagrams is to sum over all 1PI vacuum diagrams acquired using the Feynman rules derived from the shifted action
perturbatively as a sum of 1PI diagrams is to sum over all 1PI vacuum diagrams acquired using the Feynman rules derived from the shifted action  . This works because any place where
. This works because any place where  appears in any of the propagators or vertices is a place where an external
appears in any of the propagators or vertices is a place where an external  line could be attached.
line could be attached.
 approximation to the action can be found by considering the expansion of the partition function around the classical vacuum expectation value field configuration
approximation to the action can be found by considering the expansion of the partition function around the classical vacuum expectation value field configuration  , yielding the
, yielding the ![{\displaystyle \Gamma =S+{\frac {i}{2}}{\text{Tr}}{\bigg }{\delta \phi (x)\delta \phi (y)}}{\bigg |}_{\phi =\phi _{\text{cl}}}{\bigg ]}+\cdots .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4d33b99279cd472089ea2d2ae99a1e6646f76ff)





 acquired via perturbation theory must be corrected to the true effective potential
acquired via perturbation theory must be corrected to the true effective potential  , shown via dashed lines in region where the two disagree.
, shown via dashed lines in region where the two disagree. satisfying
satisfying  . This definition over a large set of states is necessary because multiple different states may result in the same expectation value. It can further be shown that the effective potential is necessarily a
. This definition over a large set of states is necessary because multiple different states may result in the same expectation value. It can further be shown that the effective potential is necessarily a  .
.
 and
and  are the expectation values for the states
are the expectation values for the states  and
and  , respectively. Then any
, respectively. Then any  using
using

 meaning
meaning