This is an old revision of this page, as edited by Rebroad (talk | contribs) at 14:27, 12 February 2007 (←Undid revision 107562401 by Atlant (talk) - Refer to talk page - there is an ongoing dispute.). The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.
Revision as of 14:27, 12 February 2007 by Rebroad (talk | contribs) (←Undid revision 107562401 by Atlant (talk) - Refer to talk page - there is an ongoing dispute.)(diff) ← Previous revision | Latest revision (diff) | Newer revision → (diff)| The neutrality of this article is disputed. Relevant discussion may be found on the talk page. Please do not remove this message until conditions to do so are met. (Learn how and when to remove this message) |
Radiocarbon dating is a radiometric dating method that uses the naturally occurring isotope carbon-14 to determine the age of carbonaceous materials up to about 60,000 years. Raw, i.e. uncalibrated, radiocarbon ages are usually reported in radiocarbon years "Before Present" (BP), "Present" being defined as AD 1950. Such raw ages can be calibrated to give calendar dates.
The technique of radiocarbon dating was discovered by Willard Frank Libby and his colleagues in 1949 during his tenure as a professor at the University of Chicago. Libby estimated that the steady state radioactivity concentration of exchangeable carbon-14 would be about 14 disintegrations per minute (dpm) per gram carbon (ca 230 mBq/g). In 1960, Libby was awarded the Nobel Prize in chemistry for his method to use carbon-14 (C) for age determination.
Furthering the technique and applications
Hessel de Vries, at the University of Groningen furthered the detection methods and applications to a variety of sciences. He has been called "the unsung hero of radiocarbon dating" (cf Willis).
Basic physics
Carbon has two stable, nonradioactive isotopes: carbon-12 (C), and carbon-13 (C). In addition, there are tiny amounts of the unstable isotope carbon-14 (C) on Earth. Carbon-14 has a half-life of 5730 years and would have long ago vanished from Earth were it not for the unremitting cosmic ray impacts on nitrogen in the Earth's atmosphere, which forms more of the isotope. (In fact the same process occurs in the nitrogen-rich atmosphere of Saturn's moon Titan.) When cosmic rays enter the atmosphere, they undergo various transformations, including the production of neutrons. The resulting neutrons participate in the following reaction on one of the N atoms being knocked out of a nitrogen (N2) molecule in the atmosphere:
- n + N → C + p

The highest rate of carbon-14 production takes place at altitudes of 9 to 15 km (30,000 to 50,000 ft), and at high geomagnetic latitudes, but the carbon-14 spreads evenly throughout the atmosphere and reacts with oxygen to form carbon dioxide. Carbon dioxide also permeates the oceans, dissolving in the water. For approximate analysis it is assumed that the cosmic ray flux is constant over long periods of time; thus carbon-14 could be assumed to be continuously produced at a constant rate and therefore that the proportion of radioactive to non-radioactive carbon throughout the Earth's atmosphere and surface oceans is constant: ca. 1 part per trillion (600 billion atoms/mole). For more accurate work, the temporal variations of the atmospheric radiocarbon are compensated for by means of calibration curves. When these curves are used, their accuracy and shape are the factors that determine the accuracy and age obtained for a given sample.
Plants take up atmospheric carbon dioxide by photosynthesis, and are eaten by animals, so every living thing is constantly exchanging carbon-14 with its environment as long as it lives. Once it dies, however, this exchange stops, and the amount of carbon-14 gradually decreases through radioactive decay.
- C → N + β
By emitting a β particle (beta decay), carbon-14 is changed into stable (non-radioactive) nitrogen-14. This decay can be used to get a measure of how long ago a piece of once-living material died. However, aquatic plants obtain some of their carbon from dissolved carbonates which are likely to be very old, and thus deficient in the carbon-14 isotope, so the method is less reliable for such materials as well as for samples derived from animals with such plants in their food chain.
Measurements and scales
Measurements are traditionally made by counting the radioactive decay of individual carbon atoms by gas proportional counting or by liquid scintillation counting, but these are relatively insensitive and subject to relatively large statistical uncertainties for small samples (below about 1g carbon). If there is little carbon-14 to begin with, a half-life that long means that very few of the atoms will decay while their detection is attempted (4 atoms/s) /mol just after death, hence e.g. 1 (atom/s)/mol after 10,000 years). Sensitivity has since been greatly increased by the use of accelerator-based mass-spectrometric (AMS) techniques, where all the C atoms can be counted directly, rather than only those decaying during the counting interval allotted for each analysis. The AMS technique allows one to date samples containing only a few milligrams of carbon.
Raw radiocarbon ages (i.e., those not calibrated) are usually reported in years "before present" (BP). This is the number of radiocarbon years before 1950, based on a nominal (and assumed constant - see "calibration" below) level of carbon-14 in the atmosphere equal to the 1950 level. They are also based on a slightly off historic value for the half-life maintained for consistency with older publications (see "Radiocarbon half-life" below). See the Note below for the basis of the computations. Corrections for isotopic fractionation have not been included in the present note.
Radiocarbon labs generally report an uncertainty, e.g., 3000±30BP indicates a standard deviation of 30 radiocarbon years. Traditionally this includes only the statistical counting uncertainty and some labs supply an "error multiplier" that can be multiplied by the uncertainty to account for other sources of error in the measuring process. Additional error is likely to arise from the nature and collection of the sample itself, e.g., a tree may accumulate carbon over a significant period of time. Such old wood, turned into an artifact some time after the death of the tree, will reflect the date of the carbon in the wood.
The current maximum radiocarbon age limit lies in the range between 58,000 and 62,000 years. This limit is encountered when the radioactivity of the residual C in a sample is too low to be distinguished from the background radiation.
Calibration
The need for calibration
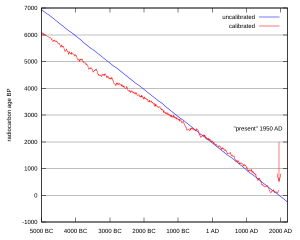
A raw BP date cannot be used directly as a calendar date, because the level of atmospheric C has not been strictly constant during the span of time that can be radiocarbon dated. The level is affected by variations in the cosmic ray intensity which is affected by variations caused by solar storms. In addition there are substantial reservoirs of carbon in organic matter, the ocean, ocean sediments (see methane hydrate), and sedimentary rocks. Changing climate can sometimes disrupt the carbon flow between these reservoirs and the atmosphere. The level has also been affected by human activities—it was almost doubled for a short period due to atomic bomb tests in the 1950s and 1960s and has been reduced by the release of large amounts of CO2 from ancient organic sources where C is not present—the fossil fuels used in industry and transportation, known as the Suess effect.
The atmospheric C concentration may be differing substantially from local water reservoirs concentration. Eroded from CaC03 or organic deposits old carbon may be easily assimilated and provide diluted C carbon into trophic chains.
Calibration methods
The raw radiocarbon dates, in BP years, are therefore calibrated to give calendar dates. Standard calibration curves are available, based on comparison of radiocarbon dates of samples that can be independently dated by other methods such as examination of tree growth rings (dendrochronology), ice cores, deep ocean sediment cores, lake sediment varves, coral samples, and speleothems (cave deposits).
The calibration curves can vary significantly from a straight line, so comparison of uncalibrated radiocarbon dates (e.g., plotting them on a graph or subtracting dates to give elapsed time) is likely to give misleading results. There are also significant plateaus in the curves, such as the one from 11,000 to 10,000 radiocarbon years BP, which is believed to be associated with changing ocean circulation during the Younger Dryas period. The accuracy of radiocarbon dating is lower for samples originating from such plateau periods. It has been noted that the plateau itself can be used as a time marker when it appears in a time series.
Radiocarbon half-life
Libby vs Cambridge values
Carbon dating was developed by a team led by Willard Libby. Originally a carbon-14 half-life of 5568±30 years was used, which is now known as the Libby half-life. Later a more accurate figure of 5730±40 years was determined, which is known as the Cambridge half-life. However laboratories continue to use the Libby figure to avoid inconsistencies when comparing raw dates and when using calibration curves to obtain calendrical dates.
Notes
Computations of ages and dates
The radioactive decay of carbon-14 follows an exponential decay. A quantity is said to be subject to exponential decay if it decreases at a rate proportional to its value. Symbolically, this can be expressed as the following differential equation, where N is the quantity and λ is a positive number called the decay constant:
The solution to this equation is:
- ,
where, for a given sample of carbonaceous matter:
- = number of radiocarbon atoms at , i.e. the origin of the disintegration time,
- = number of radiocarbon atoms remaining after radioactive decay during the time ,
- radiocarbon decay or disintegration constant.
- Two related times can be defined:
- mean- or average-life: mean or average time each radiocarbon atom spends in a given sample until it decays.
- half-life: time lapsed for half the number of radiocarbon atoms in a given sample, to decay,
It can be shown that:
- = = radiocarbon mean- or average-life = 8033 years (Libby value)
- = = radiocarbon half-life = 5568 years (Libby value)
Notice that dates are customarily given in years BP which implies t(BP) = -t because the time arrow for dates runs in reverse direction from the time arrow for the corresponding ages. From these considerations and the above equation, it results:
For a raw radiocarbon date:
and for a raw radiocarbon age:
After replacing values, the raw radiocarbon age becomes any of the following equivalent formulae:
using logs base e and the average life:
and
using logs base 2 and the half-life:
Speleothem studies in the Bahamas extend C14 calibration
Relatively recent (2001) evidence has allowed scientists to refine the knowledge of one of the underlying assumptions. A peak in the amount of carbon-14 was discovered by scientists studying speleothems in caves in the Bahamas. Stalagmites are calcium carbonate deposits left behind when seepage water, containing dissolved carbon dioxide, evaporates. Carbon-14 levels were found to be twice as high as modern levels. These discoveries improved the calibration for the radiocarbon technique and extended its usefulness to 45,000 years into the past.
Controversy
Carbon dating is extremely controversial amongst fundamental religious believers such as creationists. It can be used to prove the existence of items older than the supposed age of the Earth. Creationist scientists have questioned its accuracy although none of their research has yet been subject to satisfactory peer review.
Examples
- Ancient footprints of Acahualinca
- Haraldskær Woman
- Kennewick Man
- Skeleton Lake
- Shroud of Turin
- Thera eruption
- Vinland map
See also
- Age of the Earth
- Absolute dating
- Cosmogenic isotopes
- Environmental isotopes
- Radiometric dating
- Relative dating
- Discussion of half-life and average-life or mean-lifetime
References
- http://www.ingentaconnect.com/content/arizona/rdc/2001/00000043/00000002/art00008] Plastino, Wolfango; Kaihola, Lauri; Bartolomei, Paolo; Bella, Francesco, COSMIC BACKGROUND REDUCTION IN THE RADIOCARBON MEASUREMENT BY SCINTILLATION SPECTROMETRY AT THE UNDERGROUND LABORATORY OF GRAN SASSO, Radiocarbon, Volume 43, Issue 2, (May 2001) pp. 157-161
- http://physicsweb.org/articles/news/5/5/7/1 Katie Pennicott, Carbon clock could show the wrong time, PhysicsWeb, 10 May 2001
- Mari N. Jensen, By studying a stalagmite from a cave in the Bahamas, UA researchers provide a more accurate way for radiocarbon dating to find the ages of ancient artifacts., in http://www.physics.arizona.edu/physics/public/beck-citizen.html, The University of Arizona, Department of Physics (2001)
- J. R. Arnold and W. F. Libby, "Age Determinations by Radiocarbon Content: Checks with Samples of Known Age", Science, Vol. 110 (1949).
- Bowman, Sheridan, Interpreting the Past: Radiocarbon Dating, University of California Press, 1990, ISBN 0-520-07037-2
- Currie, Lloyd. The Remarkable Metrological History of Radiocarbon Dating .
- Michael Friedrich, Sabine Remmele, Bernd Kromer, Jutta Hofmann, Marco Spurk, Klaus Felix Kaiser, Christian Orcel, Manfred Küppers: "The 12,460-Year Hohenheim Oak and Pine Tree-Ring Chronology from Central Europe—a Unique Annual Record for Radiocarbon Calibration and Paleoenvironment Reconstructions", Radiocarbon 46/3, S. 1111-1122 (2004).
- Harry E. Gove: From Hiroshima to the Iceman. The Development and Applications of Accelerator Mass Spectrometry. Bristol: Institute of Physics Publishing, 1999.
- Kovar, Anton J. Problems in Radiocarbon Dating at Teotihuacan. American Antiquity, Vol. 31, No. 3, Part 1 (Jan., 1966) , pp. 427-430 .
- Libby, W. F., Radiocarbon Dating, 2nd ed. (Univ. of Chicago Press, Chicago, Ill.,. 175 pp., 1955).
- Lorenz,R. D., A. J. T .Jull, J. I. Lunine and T. Swindle (2002),Radiocarbon on Titan, Meteoritics and Planetary Science, 37, 867-874
- Mook, Willem G and van der Plicht, Johannes (1999), "Reporting 14C activities and concentrations", Radiocarbon 41: 227–239.
- The Discovery of Global Warming, by Spencer Weart
- Willis E.H. (1996), Radiocarbon dating in Cambridge: some personal recollections. A Worm's Eye View of the Early Days,
External links
- Carbon Dating
- Radiocarbon - The main international journal of record for research articles and date lists relevant to 14C
- C14dating.com - General information on Radiocarbon dating
- K12 section of the Radiocarbon WEBinfo site
- NOSAMS: National Ocean Sciences Accelerator Mass Spectrometry Facility at the Woods Hole Oceanographic Institution.
- Several calibration programs can be found at www.radiocarbon.org
- CalPal - Cologne Radiocarbon Calibration & Paleoclimate Research Package
- OxCal (Oxford Calibration) program
- Discussion of calibration
- Fairbanks' Radiocarbon age to calendar age conversion program
- CalPal Online
- Further basic information on radiocarbon dating (PDF)
- Willard Frank Libby biography
Template:Link FA Template:Link FA
Categories:
 ,
, = number of radiocarbon atoms at
= number of radiocarbon atoms at  , i.e. the origin of the disintegration time,
, i.e. the origin of the disintegration time, = number of radiocarbon atoms remaining after radioactive decay during the time
= number of radiocarbon atoms remaining after radioactive decay during the time  ,
, radiocarbon decay or disintegration constant.
radiocarbon decay or disintegration constant. =
=  = radiocarbon mean- or average-life = 8033 years (Libby value)
= radiocarbon mean- or average-life = 8033 years (Libby value) =
=  = radiocarbon half-life = 5568 years (Libby value)
= radiocarbon half-life = 5568 years (Libby value)


