This is an old revision of this page, as edited by Zac67 (talk | contribs) at 18:51, 9 September 2022 (Reverted 1 edit by 2003:D7:DF0B:AA00:76D4:35FF:FE54:CF0D (talk) to last revision by Hairy Dude). The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.
Revision as of 18:51, 9 September 2022 by Zac67 (talk | contribs) (Reverted 1 edit by 2003:D7:DF0B:AA00:76D4:35FF:FE54:CF0D (talk) to last revision by Hairy Dude)(diff) ← Previous revision | Latest revision (diff) | Newer revision → (diff) Any of a set of standard configurations of Redundant Arrays of Independent DisksIn computer storage, the standard RAID levels comprise a basic set of RAID ("redundant array of independent disks" or "redundant array of inexpensive disks") configurations that employ the techniques of striping, mirroring, or parity to create large reliable data stores from multiple general-purpose computer hard disk drives (HDDs). The most common types are RAID 0 (striping), RAID 1 (mirroring) and its variants, RAID 5 (distributed parity), and RAID 6 (dual parity). Multiple RAID levels can also be combined or nested, for instance RAID 10 (striping of mirrors) or RAID 01 (mirroring stripe sets). RAID levels and their associated data formats are standardized by the Storage Networking Industry Association (SNIA) in the Common RAID Disk Drive Format (DDF) standard. The numerical values only serve as identifiers and do not signify performance, reliability, generation, or any other metric.
While most RAID levels can provide good protection against and recovery from hardware defects or defective sectors/read errors (hard errors), they do not provide any protection against data loss due to catastrophic failures (fire, water) or soft errors such as user error, software malfunction, or malware infection. For valuable data, RAID is only one building block of a larger data loss prevention and recovery scheme – it cannot replace a backup plan.
RAID 0
See also: JBOD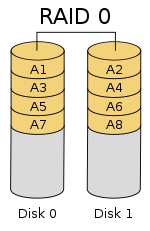
RAID 0 (also known as a stripe set or striped volume) splits ("stripes") data evenly across two or more disks, without parity information, redundancy, or fault tolerance. Since RAID 0 provides no fault tolerance or redundancy, the failure of one drive will cause the entire array to fail; as a result of having data striped across all disks, the failure will result in total data loss. This configuration is typically implemented having speed as the intended goal. RAID 0 is normally used to increase performance, although it can also be used as a way to create a large logical volume out of two or more physical disks.
A RAID 0 setup can be created with disks of differing sizes, but the storage space added to the array by each disk is limited to the size of the smallest disk. For example, if a 120 GB disk is striped together with a 320 GB disk, the size of the array will be 120 GB × 2 = 240 GB. However, some RAID implementations allow the remaining 200 GB to be used for other purposes.
The diagram in this section shows how the data is distributed into stripes on two disks, with A1:A2 as the first stripe, A3:A4 as the second one, etc. Once the stripe size is defined during the creation of a RAID 0 array, it needs to be maintained at all times. Since the stripes are accessed in parallel, an n-drive RAID 0 array appears as a single large disk with a data rate n times higher than the single-disk rate.
Performance
A RAID 0 array of n drives provides data read and write transfer rates up to n times as high as the individual drive rates, but with no data redundancy. As a result, RAID 0 is primarily used in applications that require high performance and are able to tolerate lower reliability, such as in scientific computing or computer gaming.
Some benchmarks of desktop applications show RAID 0 performance to be marginally better than a single drive. Another article examined these claims and concluded that "striping does not always increase performance (in certain situations it will actually be slower than a non-RAID setup), but in most situations it will yield a significant improvement in performance". Synthetic benchmarks show different levels of performance improvements when multiple HDDs or SSDs are used in a RAID 0 setup, compared with single-drive performance. However, some synthetic benchmarks also show a drop in performance for the same comparison.
RAID 1
See also: RAID 1E
RAID 1 consists of an exact copy (or mirror) of a set of data on two or more disks; a classic RAID 1 mirrored pair contains two disks. This configuration offers no parity, striping, or spanning of disk space across multiple disks, since the data is mirrored on all disks belonging to the array, and the array can only be as big as the smallest member disk. This layout is useful when read performance or reliability is more important than write performance or the resulting data storage capacity.
The array will continue to operate so long as at least one member drive is operational.
Performance
Any read request can be serviced and handled by any drive in the array; thus, depending on the nature of I/O load, random read performance of a RAID 1 array may equal up to the sum of each member's performance, while the write performance remains at the level of a single disk. However, if disks with different speeds are used in a RAID 1 array, overall write performance is equal to the speed of the slowest disk.
Synthetic benchmarks show varying levels of performance improvements when multiple HDDs or SSDs are used in a RAID 1 setup, compared with single-drive performance. However, some synthetic benchmarks also show a drop in performance for the same comparison.
RAID 2

RAID 2, which is rarely used in practice, stripes data at the bit (rather than block) level, and uses a Hamming code for error correction. The disks are synchronized by the controller to spin at the same angular orientation (they reach index at the same time), so it generally cannot service multiple requests simultaneously. However, depending with a high rate Hamming code, many spindles would operate in parallel to simultaneously transfer data so that "very high data transfer rates" are possible as for example in the DataVault where 32 data bits were transmitted simultaneously.
With all hard disk drives implementing internal error correction, the complexity of an external Hamming code offered little advantage over parity so RAID 2 has been rarely implemented; it is the only original level of RAID that is not currently used.
RAID 3

RAID 3, which is rarely used in practice, consists of byte-level striping with a dedicated parity disk. One of the characteristics of RAID 3 is that it generally cannot service multiple requests simultaneously, which happens because any single block of data will, by definition, be spread across all members of the set and will reside in the same physical location on each disk. Therefore, any I/O operation requires activity on every disk and usually requires synchronized spindles.
This makes it suitable for applications that demand the highest transfer rates in long sequential reads and writes, for example uncompressed video editing. Applications that make small reads and writes from random disk locations will get the worst performance out of this level.
The requirement that all disks spin synchronously (in a lockstep) added design considerations that provided no significant advantages over other RAID levels. Both RAID 3 and RAID 4 were quickly replaced by RAID 5. RAID 3 was usually implemented in hardware, and the performance issues were addressed by using large disk caches.
RAID 4

RAID 4 consists of block-level striping with a dedicated parity disk. As a result of its layout, RAID 4 provides good performance of random reads, while the performance of random writes is low due to the need to write all parity data to a single disk, unless the filesystem is RAID-4-aware and compensates for that.
An advantage of RAID 4 is that it can be quickly extended online, without parity recomputation, as long as the newly added disks are completely filled with 0-bytes.
In diagram 1, a read request for block A1 would be serviced by disk 0. A simultaneous read request for block B1 would have to wait, but a read request for B2 could be serviced concurrently by disk 1.
RAID 5
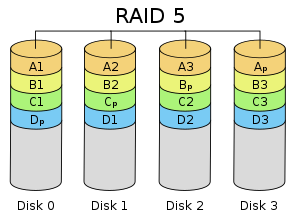
RAID 5 consists of block-level striping with distributed parity. Unlike in RAID 4, parity information is distributed among the drives. It requires that all drives but one be present to operate. Upon failure of a single drive, subsequent reads can be calculated from the distributed parity such that no data is lost. RAID 5 requires at least three disks.
There are many layouts of data and parity in a RAID 5 disk drive array depending upon the sequence of writing across the disks, that is:
- the sequence of data blocks written, left to right or right to left on the disk array, of disks 0 to N, and
- the location of the parity block at the beginning or end of the stripe, and
- the location of the first block of a stripe with respect to parity of the previous stripe.
The figure to the right shows 1) data blocks written left to right, 2) the parity block at the end of the stripe and 3) the first block of the next stripe not on the same disk as the parity block of the previous stripe. It can be designated as a Left Asynchronous RAID 5 layout and this is the only layout identified in the last edition of The Raid Book published by the defunct Raid Advisory Board. In a Synchronous layout the data first block of the next stripe is written on the same drive as the parity block of the previous stripe.
In comparison to RAID 4, RAID 5's distributed parity evens out the stress of a dedicated parity disk among all RAID members. Additionally, write performance is increased since all RAID members participate in the serving of write requests. Although it will not be as efficient as a striping (RAID 0) setup, because parity must still be written, this is no longer a bottleneck.
Since parity calculation is performed on the full stripe, small changes to the array experience write amplification: in the worst case when a single, logical sector is to be written, the original sector and the according parity sector need to be read, the original data is removed from the parity, the new data calculated into the parity and both the new data sector and the new parity sector are written.
RAID 6

RAID 6 extends RAID 5 by adding another parity block; thus, it uses block-level striping with two parity blocks distributed across all member disks.
As in RAID 5, there are many layouts of RAID 6 disk arrays depending upon the direction the data blocks are written, the location of the parity blocks with respect to the data blocks and whether or not the first data block of a subsequent stripe is written to the same drive as the last parity block of the prior stripe. The figure to the right is just one of many such layouts.
According to the Storage Networking Industry Association (SNIA), the definition of RAID 6 is: "Any form of RAID that can continue to execute read and write requests to all of a RAID array's virtual disks in the presence of any two concurrent disk failures. Several methods, including dual check data computations (parity and Reed–Solomon), orthogonal dual parity check data and diagonal parity, have been used to implement RAID Level 6."
Performance
RAID 6 does not have a performance penalty for read operations, but it does have a performance penalty on write operations because of the overhead associated with parity calculations. Performance varies greatly depending on how RAID 6 is implemented in the manufacturer's storage architecture—in software, firmware, or by using firmware and specialized ASICs for intensive parity calculations. RAID 6 can read up to the same speed as RAID 5 with the same number of physical drives.
When either diagonal or orthogonal dual parity is used, a second parity calculation is necessary for write operations. This doubles CPU overhead for RAID-6 writes, versus single-parity RAID levels. When a Reed Solomon code is used, the second parity calculation is unnecessary. Reed Solomon has the advantage of allowing all redundancy information to be contained within a given stripe.
Simplified parity example
Suppose we would like to distribute our data over chunks. Our goal is to define two parity values and , known as syndromes, resulting in a system of physical drives that is resilient to the loss of any two of them. In order to generate more than a single independent syndrome, we will need to perform our parity calculations on data chunks of size A typical choice in practice is a chunk size , i.e. striping the data per-byte. We will denote the base-2 representation of a data chunk as , where each is either 0 or 1.
If we are using a small number of chunks , we can use a simple parity computation, which will help motivate the use of the Reed–Solomon system in the general case. For our first parity value , we compute the simple XOR of the data across the stripes, as with RAID 5. This is written where denotes the XOR operator. The second parity value is analogous, but with each data chunk bit-shifted a different amount. Writing , we define In the event of a single drive failure, the data can be recomputed from just like with RAID 5. We will show we can also recover from simultaneous failure of 2 drives. If we lose a data chunk and , we can recover from and the remaining data by using the fact that . Suppose on a system of chunks, the drive containing chunk has failed. We can compute
and recover the lost data by undoing the bit shift. We can also recover from the failure of two data disks by computing the XOR of and with the remaining data. If in the previous example, chunk had been lost as well, we would computeOn a bitwise level, this represents a system of equations in unknowns which uniquely determine the lost data.
This system will no longer work applied to a larger number of drives . This is because if we repeatedly apply the shift operator times to a chunk of length , we end up back where we started. If we tried to apply the algorithm above to a system containing data disks, the right-hand side of the second equation would be , which is the same as the first set of equations. This would only yield half as many equations as needed to solve for the missing values.
General parity system
It is possible to support a far greater number of drives by choosing the parity function more carefully. The issue we face is to ensure that a system of equations over the finite field has a unique solution, so we will turn to the theory of polynomial equations. Consider the Galois field with . This field is isomorphic to a polynomial field for a suitable irreducible polynomial of degree over . We will represent the data elements as polynomials in the Galois field. Let correspond to the stripes of data across hard drives encoded as field elements in this manner. We will use to denote addition in the field, and concatenation to denote multiplication. The reuse of is intentional: this is because addition in the finite field represents to the XOR operator, so computing the sum of two elements is equivalent to computing XOR on the polynomial coefficients.
A generator of a field is an element of the field such that is different for each non-negative . This means each element of the field, except the value , can be written as a power of A finite field is guaranteed to have at least one generator. Pick one such generator , and define and as follows:
As before, the first checksum is just the XOR of each stripe, though interpreted now as a polynomial. The effect of can be thought of as the action of a carefully chosen linear feedback shift register on the data chunk. Unlike the bit shift in the simplified example, which could only be applied times before the encoding began to repeat, applying the operator multiple times is guaranteed to produce unique invertible functions, which will allow a chunk length of to support up to data pieces.
If one data chunk is lost, the situation is similar to the one before. In the case of two lost data chunks, we can compute the recovery formulas algebraically. Suppose that and are the lost values with , then, using the other values of , we find constants and :
We can solve for in the second equation and plug it into the first to find , and then .
Unlike P, The computation of Q is relatively CPU intensive, as it involves polynomial multiplication in . This can be mitigated with a hardware implementation or by using an FPGA.
Comparison
See also: Nested RAID levels § ComparisonThe following table provides an overview of some considerations for standard RAID levels. In each case, array space efficiency is given as an expression in terms of the number of drives, n; this expression designates a fractional value between zero and one, representing the fraction of the sum of the drives' capacities that is available for use. For example, if three drives are arranged in RAID 3, this gives an array space efficiency of 1 − 1/n = 1 − 1/3 = 2/3 ≈ 67%; thus, if each drive in this example has a capacity of 250 GB, then the array has a total capacity of 750 GB but the capacity that is usable for data storage is only 500 GB. Different RAID configurations can also detect failure during so called data scrubbing.
Historically disks were subject to lower reliability and RAID levels were also used to detect which disk in the array had failed in addition to that a disk had failed. Though as noted by Patterson et. al. even at the inception of RAID many (though not all) disks were already capable of finding internal errors using error correcting codes. In particular it is/was sufficient to have a mirrored set of disks to detect a failure, but two disks were not sufficient to detect which had failed in a disk array without error correcting features. Modern RAID arrays depend for the most part on a disk's ability to identify itself as faulty which can be detected as part of a scrub. The redundant information is used to reconstruct the missing data, rather than to identify the faulted drive. Drives are considered to have faulted if they experience an unrecoverable read error, which occurs after a drive has retried many times to read data and failed. Enterprise drives may also report failure in far fewer tries than consumer drives as part of TLER to ensure a read request is fulfilled in a timely manner.
| Level | Description | Minimum number of drives | Space efficiency | Fault tolerance | Fault isolation | Read performance | Write performance |
|---|---|---|---|---|---|---|---|
| as factor of single disk | |||||||
| RAID 0 | Block-level striping without parity or mirroring | 2 | 1 | None | Drive Firmware Only | n | n |
| RAID 1 | Mirroring without parity or striping | 2 | 1/n | n − 1 drive failures | Drive Firmware or voting if n > 2 | n | 1 |
| RAID 2 | Bit-level striping with Hamming code for error correction | 3 | 1 − 1/n log2 (n + 1) | One drive failure | Drive Firmware and Parity | Depends | Depends |
| RAID 3 | Byte-level striping with dedicated parity | 3 | 1 − 1/n | One drive failure | Drive Firmware and Parity | n − 1 | n − 1 |
| RAID 4 | Block-level striping with dedicated parity | 3 | 1 − 1/n | One drive failure | Drive Firmware and Parity | n − 1 | n − 1 |
| RAID 5 | Block-level striping with distributed parity | 3 | 1 − 1/n | One drive failure | Drive Firmware and Parity | n | single sector: 1/4 full stripe: n − 1 |
| RAID 6 | Block-level striping with double distributed parity | 4 | 1 − 2/n | Two drive failures | Drive Firmware and Parity | n | single sector: 1/6 full stripe: n − 2 |
System implications
In measurement of the I/O performance of five filesystems with five storage configurations—single SSD, RAID 0, RAID 1, RAID 10, and RAID 5 it was shown that F2FS on RAID 0 and RAID 5 with eight SSDs outperforms EXT4 by 5 times and 50 times, respectively. The measurements also suggest that the RAID controller can be a significant bottleneck in building a RAID system with high speed SSDs.
Nested RAID
Main article: Nested RAID levelsCombinations of two or more standard RAID levels. They are also known as RAID 0+1 or RAID 01, RAID 0+3 or RAID 03, RAID 1+0 or RAID 10, RAID 5+0 or RAID 50, RAID 6+0 or RAID 60, and RAID 10+0 or RAID 100.
Non-standard variants
Main articles: Non-standard RAID levels and Non-RAID drive architecturesIn addition to standard and nested RAID levels, alternatives include non-standard RAID levels, and non-RAID drive architectures. Non-RAID drive architectures are referred to by similar terms and acronyms, notably JBOD ("just a bunch of disks"), SPAN/BIG, and MAID ("massive array of idle disks").
Notes
- ^ Theoretical maximum, as low as single-disk performance in practice
- Assumes a non-degenerate minimum number of drives
- If disks with different speeds are used in a RAID 1 array, overall write performance is equal to the speed of the slowest disk.
- RAID 2 can recover from one drive failure or repair corrupt data or parity when a corrupted bit's corresponding data and parity are good.
- ^ Assumes hardware capable of performing associated calculations fast enough
References
- "Common raid Disk Data Format (DDF)". SNIA.org. Storage Networking Industry Association. Retrieved 2013-04-23.
- "RAID 0 Data Recovery". DataRecovery.net. Retrieved 2015-04-30.
- "Understanding RAID". CRU-Inc.com. Retrieved 2015-04-30.
- "How to Combine Multiple Hard Drives Into One Volume for Cheap, High-Capacity Storage". LifeHacker.com. 2013-02-26. Retrieved 2015-04-30.
- ^ Chen, Peter; Lee, Edward; Gibson, Garth; Katz, Randy; Patterson, David (1994). "RAID: High-Performance, Reliable Secondary Storage". ACM Computing Surveys. 26 (2): 145–185. CiteSeerX 10.1.1.41.3889. doi:10.1145/176979.176981. S2CID 207178693.
- de Kooter, Sebastiaan (2015-04-13). "Gaming storage shootout 2015: SSD, HDD or RAID 0, which is best?". GamePlayInside.com. Retrieved 2015-09-22.
- "Western Digital's Raptors in RAID-0: Are two drives better than one?". AnandTech.com. AnandTech. July 1, 2004. Retrieved 2007-11-24.
- "Hitachi Deskstar 7K1000: Two Terabyte RAID Redux". AnandTech.com. AnandTech. April 23, 2007. Retrieved 2007-11-24.
- "RAID 0: Hype or blessing?". Tweakers.net. Persgroep Online Services. August 7, 2004. Retrieved 2008-07-23.
- "Does RAID0 Really Increase Disk Performance?". HardwareSecrets.com. November 1, 2006.
- ^ Larabel, Michael (2014-10-22). "Btrfs RAID HDD Testing on Ubuntu Linux 14.10". Phoronix. Retrieved 2015-09-19.
- ^ Larabel, Michael (2014-10-29). "Btrfs on 4 × Intel SSDs In RAID 0/1/5/6/10". Phoronix. Retrieved 2015-09-19.
- "FreeBSD Handbook: 19.3. RAID 1 – Mirroring". FreeBSD.org. 2014-03-23. Retrieved 2014-06-11.
- ^ "Which RAID Level is Right for Me?: RAID 1 (Mirroring)". Adaptec.com. Adaptec. Retrieved 2014-01-02.
- ^ "Selecting the Best RAID Level: RAID 1 Arrays (Sun StorageTek SAS RAID HBA Installation Guide)". Docs.Oracle.com. Oracle Corporation. 2010-12-23. Retrieved 2014-01-02.
- "RAID 2". Techopedia. Techopedia. Retrieved 11 December 2019.
- ^ Vadala, Derek (2003). Managing RAID on Linux. O'Reilly Series (illustrated ed.). O'Reilly. p. 6. ISBN 9781565927308.
- ^ Marcus, Evan; Stern, Hal (2003). Blueprints for high availability (2, illustrated ed.). John Wiley and Sons. p. 167. ISBN 9780471430261.
- The RAIDbook, 4th Edition, The RAID Advisory Board, June 1995, p.101
- Meyers, Michael; Jernigan, Scott (2003). Mike Meyers' A+ Guide to Managing and Troubleshooting PCs (illustrated ed.). McGraw-Hill Professional. p. 321. ISBN 9780072231465.
- Natarajan, Ramesh (2011-11-21). "RAID 2, RAID 3, RAID 4 and RAID 6 Explained with Diagrams". TheGeekStuff.com. Retrieved 2015-01-02.
- "RAID 5 Data Recovery FAQ". VantageTech.com. Vantage Technologies. Retrieved 2014-07-16.
- ^ "RAID Information - Linux RAID-5 Algorithms". Ashford computer Consulting Service. Retrieved February 16, 2021.
- Massigilia, Paul (February 1997). The RAID Book, 6th Edition. RAID Advisory Board. pp. 101–129.
- "Welcome to the RAID Advisory Board". RAID Advisory Board. April 6, 2001. Archived from the original on 2001-04-06. Retrieved February 16, 2021. Last valid archived webpage at Wayback Machine}}
- Koren, Israel. "Basic RAID Organizations". ECS.UMass.edu. University of Massachusetts. Retrieved 2014-11-04.
- "Sun StorageTek SAS RAID HBA Installation Guide, Appendix F: Selecting the Best RAID Level: RAID 6 Arrays". Docs.Oracle.com. 2010-12-23. Retrieved 2015-08-27.
- "Dictionary R". SNIA.org. Storage Networking Industry Association. Retrieved 2007-11-24.
- Faith, Rickard E. (13 May 2009). "A Comparison of Software RAID Types".
{{cite journal}}: Cite journal requires|journal=(help) - Anvin, H. Peter (May 21, 2009). "The Mathematics of RAID-6" (PDF). Kernel.org. Linux Kernel Organization. Retrieved November 4, 2009.
- Patterson, David A.; Gibson, Garth; Katz, Randy H. (1988). "A case for redundant arrays of inexpensive disks (RAID)" (PDF). Proceedings of the 1988 ACM SIGMOD International Conference on Management of Data - SIGMOD '88: 112. doi:10.1145/50202.50214. ISBN 0897912683. S2CID 52859427. Retrieved 25 June 2022.
A single parity disk can detect a single error, but to correct an error we need enough check disks to identify the disk with the error. Most check disks in the level 2 RAID are used to determine which disk failed, for only one redundant parity disk is needed to detect an error. These extra disks are truly "redundant" since most disk controllers can already detect If a dusk failed either through special signals provided in the disk interface or the extra checking information at the end of a sector
- "Enterprise vs Desktop Harddrives" (PDF). Intel.com. Intel. p. 10.
- Park, Chanhyun; Lee, Seongjin; Won, Youjip (2014). An Analysis on Empirical Performance of SSD-Based RAID. Vol. 2014. pp. 395–405. doi:10.1007/978-3-319-09465-6_41. ISBN 978-3-319-09464-9.
{{cite book}}:|journal=ignored (help)
Further reading
- "Learning About RAID". Support.Dell.com. Dell. 2009. Archived from the original on 2009-02-20. Retrieved 2016-04-15.
- Redundant Arrays of Inexpensive Disks (RAIDs), chapter 38 from the Operating Systems: Three Easy Pieces book by Remzi H. Arpaci-Dusseau and Andrea C. Arpaci-Dusseau
External links
- IBM summary on RAID levels
- RAID 5 parity explanation and checking tool
- RAID Calculator for Standard RAID Levels and Other RAID Tools
- Sun StorEdge 3000 Family Configuration Service 2.5 User’s Guide: RAID Basics
| RAID | |
|---|---|
| Redundant array of independent disks | |
| Disk arrays | |
| RAID levels | |
| Principles | |
| Interfaces | |
| Non-RAID drive architectures | |
 chunks. Our goal is to define two parity values
chunks. Our goal is to define two parity values  and
and  , known as
, known as  physical drives that is resilient to the loss of any two of them. In order to generate more than a single independent syndrome, we will need to perform our parity calculations on data chunks of size
physical drives that is resilient to the loss of any two of them. In order to generate more than a single independent syndrome, we will need to perform our parity calculations on data chunks of size  A typical choice in practice is a chunk size
A typical choice in practice is a chunk size  , i.e. striping the data per-byte. We will denote the base-2 representation of a data chunk
, i.e. striping the data per-byte. We will denote the base-2 representation of a data chunk  as
as  , where each
, where each  is either 0 or 1.
is either 0 or 1.
 , we can use a simple parity computation, which will help motivate the use of the Reed–Solomon system in the general case. For our first parity value
, we can use a simple parity computation, which will help motivate the use of the Reed–Solomon system in the general case. For our first parity value  where
where  denotes the XOR operator. The second parity value is analogous, but with each data chunk bit-shifted a different amount. Writing
denotes the XOR operator. The second parity value is analogous, but with each data chunk bit-shifted a different amount. Writing  , we define
, we define  In the event of a single drive failure, the data can be recomputed from
In the event of a single drive failure, the data can be recomputed from  . Suppose on a system of
. Suppose on a system of  chunks, the drive containing chunk
chunks, the drive containing chunk  has failed. We can compute
has failed. We can compute 
 had been lost as well, we would compute
had been lost as well, we would compute
 On a bitwise level, this represents a system of
On a bitwise level, this represents a system of  equations in
equations in  . This is because if we repeatedly apply the shift operator
. This is because if we repeatedly apply the shift operator  times to a chunk of length
times to a chunk of length  , which is the same as the first set of equations. This would only yield half as many equations as needed to solve for the missing values.
, which is the same as the first set of equations. This would only yield half as many equations as needed to solve for the missing values.
 has a unique solution, so we will turn to the theory of polynomial equations. Consider the
has a unique solution, so we will turn to the theory of polynomial equations. Consider the  with
with  . This field is isomorphic to a polynomial field
. This field is isomorphic to a polynomial field  for a suitable
for a suitable  of degree
of degree  in the Galois field. Let
in the Galois field. Let  correspond to the stripes of data across hard drives encoded as field elements in this manner. We will use
correspond to the stripes of data across hard drives encoded as field elements in this manner. We will use  is different for each non-negative
is different for each non-negative  . This means each element of the field, except the value
. This means each element of the field, except the value  , can be written as a power of
, can be written as a power of  A finite field is guaranteed to have at least one generator. Pick one such generator
A finite field is guaranteed to have at least one generator. Pick one such generator  , and define
, and define 

 unique invertible functions, which will allow a chunk length of
unique invertible functions, which will allow a chunk length of  data pieces.
data pieces.
 and
and  are the lost values with
are the lost values with  , then, using the other values of
, then, using the other values of  and
and  :
:


 in the second equation and plug it into the first to find
in the second equation and plug it into the first to find  , and then
, and then  .
.