This is an old revision of this page, as edited by 88.153.57.155 (talk) at 22:01, 12 August 2008 (→History of zero). The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.
Revision as of 22:01, 12 August 2008 by 88.153.57.155 (talk) (→History of zero)(diff) ← Previous revision | Latest revision (diff) | Newer revision → (diff) "Zero" redirects here. For other uses, see Zero (disambiguation).| 0 | |
| Template:Numbers (digits) | |
| Cardinal | 0, zero, "oh" (IPA: [oʊ]), nought, naught, ought, nil, null |
| Ordinal | 0th, zeroth |
| Factorization | |
| Divisors | all numbers |
| Roman numeral | N/A |
| Arabic | ٠ |
| Bengali | ০ |
| Devanāgarī | ० |
| Chinese | 〇,零 |
| Japanese numeral | 〇 |
| Khmer | ០ |
| Thai | ๐ |
| Binary | 0 |
| Octal | 0 |
| Duodecimal | 0 |
| Hexadecimal | 0 |
0 (zero) is both a number and the numerical digit used to represent that number in numerals. It plays a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, zero is used as a placeholder in place value systems. In the English language, zero may also be called null, nil or naught.
0 as a number
0 is the integer preceding 1. In most systems, 0 was identified before the idea of 'negative integers' was accepted. Zero is an even number. 0 is neither positive nor negative.
Zero is a number which quantifies a count or an amount of null size; that is, if the number of your brothers is zero, that means the same thing as having no brothers, and if something has a weight of zero, it has no weight. If the difference between the number of pieces in two piles is zero, it means the two piles have an equal number of pieces. Before counting starts, the result can be assumed to be zero; that is the number of items counted before you count the first item and counting the first item brings the result to one. And if there are no items to be counted, zero remains the final result.
Almost all historians omit the year zero from the proleptic Gregorian and Julian calendars, but astronomers include it in these same calendars. However, the phrase Year Zero may be used to describe any event considered so significant that it serves as a new base point in time.
0 as a digit
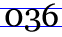
The modern numerical digit 0 is usually written as a circle, an ellipse, or a rounded rectangle. In most modern typefaces, the height of the 0 character is the same as the other digits. However, in typefaces with text figures, the character is often less tall (x-height).
 |
 |
On the seven-segment displays of calculators, watches, and household appliances, 0 is usually written with six line segments, though on some historical calculator models it was written with four line segments.
The value, or number, zero is not the same as the digit zero, used in numeral systems using positional notation. Successive positions of digits have higher weights, so inside a numeral the digit zero is used to skip a position and give appropriate weights to the preceding and following digits. A zero digit is not always necessary in a positional number system, for example, in the number 02.
Distinguishing the digit 0 from the letter O

Traditionally, standard typewriters made no distinction in shape between the letter O and the digit 0; some models did not even have a separate key for the digit 0. The oval (i.e. narrower) digit 0 and more nearly circular letter O together came into prominence on modern character displays, though the distinction was already present in some print typefaces.
The digit 0 with a dot in the centre seems to have originated as an option on IBM 3270 displays. Its appearance has continued with the Windows typeface Andalé Mono. One variation used a short vertical bar instead of the dot. This could be confused with the Greek letter Theta on a badly focused display, but in practice there was no confusion because theta was not (then) a displayable character.
An alternative, the slashed zero (looking similar to the letter O other than the slash), was primarily used in hand-written coding sheets before transcription to punched cards or tape, and is also used in old-style ASCII graphic sets descended from the default typewheel on the ASR-33 Teletype. This form is similar to the symbol , or "∅" (Unicode character U+2205), representing the empty set, as well as to the letter Ø used in several Scandinavian languages.
The convention that has the letter O with a slash and the digit 0 without was advocated by SHARE, a prominent IBM user group, and recommended by IBM for writing FORTRAN programs, and by a few other early mainframe makers; this is even more problematic for Scandinavians because it means two of their letters collide. Others advocated the opposite convention, including IBM for writing Algol programs. Some Burroughs/Unisys equipment displays a digit 0 with a reversed slash. Another convention used on some early line printers left digit 0 unornamented but added a tail or hook to the capital O so that it resembled an inverted Q or cursive capital letter-O ().

Some fonts designed for use with computers made one of the capital-O–digit-0 pair more rounded and the other more angular (closer to a rectangle). The Texas Instruments TI-99/4A computer featured a more angular capital O and a more rounded digit 0, whereas others made the choice the other way around.
The typeface used on most European number plates for cars distinguishes the two symbols partially in this manner (having a more rectangular or wider shape for the capital O than the digit 0), but in several countries a further distinction is made by slitting open the digit 0 on the upper right side (as in German plates). This typeface is called fälschungserschwerende Schrift (abbr.: FE Schrift) in Germany, meaning "script which is harder to falsify". Typefaces used on United Kingdom plates do not differentiate between the two as there can never be any ambiguity if the design is correctly spaced (the vehicle "numbers" are allocated in a manner that avoids any such confusion). The same applies to postal codes in the United Kingdom.
Sometimes the digit 0 is used either exclusively, or not at all, to avoid confusion altogether. For example, confirmation numbers used by Southwest Airlines use only the capital letters O and I instead of the digits 0 and 1, while Canadian postal codes use only the digits 1 and 0 and never the capital letters O and I, although letters and numbers always alternate.
Etymology
The word "zero" came via French zéro from Venetian zero, which (together with "cipher") came via Italian zefiro from Arabic صفر, ṣafira = "it was empty", ṣifr = "zero", "nothing", which was used to translate Sanskrit śūnya ( शून्य ), meaning void or empty.
Italian zefiro already meant "west wind" from Latin and Greek zephyrus; this may have influenced the spelling when transcribing Arabic şifr. The Italian mathematician Fibonacci (c.1170-1250), who grew up in Arab North Africa and is credited with introducing the Hindu decimal system to Europe, used the term zephyrum. This became zefiro in Italian, which was contracted to zero in Venetian, the modern English word.
As the Hindu decimal zero and its new mathematics spread from the Arab world to Europe in the Middle Ages, words derived from ṣifr and zephyrus came to refer to calculation, as well as to privileged knowledge and secret codes. According to Ifrah, "in thirteenth-century Paris, a 'worthless fellow' was called a "... cifre en algorisme", i.e., an "arithmetical nothing"." From ṣifr also came French chiffre = "digit", "figure", "number", chiffrer = "to calculate or compute", chiffré= "encrypted". Today, the word in Arabic is still ṣifr, and cognates of ṣifr are common in the languages of Europe and southwest Asia.
History
By the middle of the 2nd millennium BC, the Babylonians had a sophisticated sexagesimal positional numeral system. The lack of a positional value (or zero) was indicated by a space between sexagesimal numerals. By 300 BC, a punctuation symbol (two slanted wedges) was co-opted as a placeholder in the same Babylonian system. In a tablet unearthed at Kish (dating from about 700 BC), the scribe Bêl-bân-aplu wrote his zeroes with three hooks, rather than two slanted wedges.
The Babylonian placeholder was not a true zero because it was not used alone. Nor was it used at the end of a number. Thus numbers like 2 and 120 (2×60), 3 and 180 (3×60), 4 and 240 (4×60), looked the same because the larger numbers lacked a final sexagesimal placeholder. Only context could differentiate them.
Records show that the ancient Greeks seemed unsure about the status of zero as a number. They asked themselves, "How can nothing be something?", leading to philosophical and, by the Medieval period, religious arguments about the nature and existence of zero and the vacuum. The paradoxes of Zeno of Elea depend in large part on the uncertain interpretation of zero.
The Indian scholar Pingala (circa 5th-2nd century BC) used binary numbers in the form of short and long syllables (the latter equal in length to two short syllables), making it similar to Morse code. He and his contemporary Indian scholars used the Sanskrit word śūnya to refer to zero or void.

This is the second oldest Long Count date yet discovered. The numerals 7.16.6.16.18 translate to September, 32 BC (Julian). The glyphs surrounding the date are what is thought to be one of the few surviving examples of Epi-Olmec script.
History of zero
The concept of zero as a number, and not merely a symbol for separation is attributed to India. In India, practical calculations were carried out using zero, which was treated like any other number by the 9th century CE, even in case of division.
The Mesoamerican Long Count calendar developed in south-central Mexico required the use of zero as a place-holder within its vigesimal (base-20) positional numeral system. Many different glyphs, including this partial quatrefoil—![]() —were used as a zero symbol for these Long Count dates, the earliest of which (on Stela 2 at Chiapa de Corzo, Chiapas) has a date of 36 BC. Since the eight earliest Long Count dates appear outside the Maya homeland, it is assumed that the use of zero in the Americas predated the Maya and was possibly the invention of the Olmecs. Many of the earliest Long Count dates were found within the Olmec heartland, although the Olmec civilization ended by the 4th century BC, several centuries before the earliest known Long Count dates.
—were used as a zero symbol for these Long Count dates, the earliest of which (on Stela 2 at Chiapa de Corzo, Chiapas) has a date of 36 BC. Since the eight earliest Long Count dates appear outside the Maya homeland, it is assumed that the use of zero in the Americas predated the Maya and was possibly the invention of the Olmecs. Many of the earliest Long Count dates were found within the Olmec heartland, although the Olmec civilization ended by the 4th century BC, several centuries before the earliest known Long Count dates.
Although zero became an integral part of Maya numerals, it did not influence Old World numeral systems.
The use of a blank on a counting board to represent 0 dated back in India to 4th century BC.
In China, counting rods were used for calculation since the 4th century BCE. Chinese mathematicians understood negative numbers and zero, though they had no symbol for the latter. The Nine Chapters on the Mathematical Art, which was mainly composed in the 1st century CE, stated " subtract same signed numbers, add differently signed numbers, subtract a positive number from zero to make a negative number, and subtract a negative number from zero to make a positive number."
By 130, Ptolemy, influenced by Hipparchus and the Babylonians, was using a symbol for zero (a small circle with a long overbar) within a sexagesimal numeral system otherwise using alphabetic Greek numerals. Because it was used alone, not just as a placeholder, this Hellenistic zero was perhaps the first documented use of a number zero in the Old World. However, the positions were usually limited to the fractional part of a number (called minutes, seconds, thirds, fourths, etc.)—they were not used for the integral part of a number. In later Byzantine manuscripts of Ptolemy's Syntaxis Mathematica (also known as the Almagest), the Hellenistic zero had morphed into the Greek letter omicron (otherwise meaning 70).
Another zero was used in tables alongside Roman numerals by 525 (first known use by Dionysius Exiguus), but as a word, nulla meaning "nothing," not as a symbol. When division produced zero as a remainder, nihil, also meaning "nothing," was used. These medieval zeros were used by all future medieval computists (calculators of Easter). An isolated use of the initial, N, was used in a table of Roman numerals by Bede or a colleague about 725, a zero symbol.
In 498 AD, Indian mathematician and astronomer Aryabhata stated that "Sthanam sthanam dasa gunam" or place to place in ten times in value, which may be the origin of the modern decimal-based place value notation.
The oldest known text to use a decimal place-value system, including a zero, is the Jain text from India entitled the Lokavibhâga, dated 458 AD. This text uses Sanskrit numeral words for the digits, with words such as the Sanskrit word for void for zero (see also the section Etymology above). The first known use of special glyphs for the decimal digits that includes the indubitable appearance of a symbol for the digit zero, a small circle, appears on a stone inscription found at the Chaturbhuja Temple at Gwalior in India, dated 876 CE. There are many documents on copper plates, with the same small o in them, dated back as far as the sixth century AD, but their authenticity may be doubted.
The Indian numerals and the positional number system were introduced to the Islamic civilization by Al-Khwarizmi, the founder of several branches and basic concepts of mathematics. In the words of Philip Hitti, Al-Khwarizmi's contribution to mathematics influenced mathematical thought to a greater extent. His work on algebra initiated the subject in a systematic form and also developed it to the extent of giving analytical solutions of linear and quadratic equations, which established him as the founder of Algebra. The word algebra is derived from the title of his famous book Al-Jabr wa-al-Muqabilah, and the word algorithm is derived from his name.
Al-Khwarizmi's book on arithmetic synthesized Greek and Hindu knowledge and also contained his own fundamental contribution to mathematics and science. Thus, he explained the use of zero, a numeral of fundamental importance developed by the Indians.
It was only centuries later, in the 12th century, that the Indian numeral system was introduced to the Western world through Latin translations of his Arithmetic.
Rules of Brahmagupta
The rules governing the use of zero appeared for the first time in Brahmagupta's book Brahmasputha Siddhanta (The Opening of the Universe), written in 628. Here Brahmagupta considers not only zero, but negative numbers, and the algebraic rules for the elementary operations of arithmetic with such numbers. In some instances, his rules differ from the modern standard. Here are the rules of Brahmagupta:
- The sum of zero and a negative number is negative
- The sum of zero and a positive number is positive
- The sum of zero and zero is zero.
- The sum of a positive and a negative is their difference; or, if they are equal, zero.
- A positive or negative number when divided by zero is a fraction with the zero as denominator.
- Zero divided by a negative or positive number is either zero or is expressed as a fraction with zero as numerator and the finite quantity as denominator.
- Zero divided by zero is zero.
In saying zero divided by zero is zero, Brahmagupta differs from the modern position. Mathematicians normally do not assign a value, whereas computers and calculators sometimes assign NaN, which means "not a number." Moreover, non-zero positive or negative numbers when divided by zero are either assigned no value, or a value of unsigned infinity, positive infinity, or negative infinity. Once again, these assignments are not numbers, and are associated more with computer science than pure mathematics, where in most contexts no assignment is done.
Zero as a decimal digit
- See also: History of the Hindu-Arabic numeral system.
Positional notation without the use of zero (using an empty space in tabular arrangements, or the word kha "emptiness") is known to have been in use in India from the 6th century. The earliest certain use of zero as a decimal positional digit dates to the 9th century. The glyph for the zero digit was written in the shape of a dot, and consequently called bindu ("dot").
The Indian numeral system (base 10) reached Europe in the 11th century, via the Iberian Peninsula through Spanish Muslims the Moors, together with knowledge of astronomy and instruments like the astrolabe, first imported by Gerbert of Aurillac. For this reason, the numerals came to be known in Europe as "Arabic numerals". The Italian mathematician Fibonacci or Leonardo of Pisa was instrumental in bringing the system into European mathematics in 1202, stating:
After my father's appointment by his homeland as state official in the customs house of Bugia for the Pisan merchants who thronged to it, he took charge; and in view of its future usefulness and convenience, had me in my boyhood come to him and there wanted me to devote myself to and be instructed in the study of calculation for some days. There, following my introduction, as a consequence of marvelous instruction in the art, to the nine digits of the Hindus, the knowledge of the art very much appealed to me before all others, and for it I realized that all its aspects were studied in Egypt, Syria, Greece, Sicily, and Provence, with their varying methods; and at these places thereafter, while on business. I pursued my study in depth and learned the give-and-take of disputation. But all this even, and the algorism, as well as the art of Pythagoras, I considered as almost a mistake in respect to the method of the Hindus (Modus Indorum). Therefore, embracing more stringently that method of the Hindus, and taking stricter pains in its study, while adding certain things from my own understanding and inserting also certain things from the niceties of Euclid's geometric art. I have striven to compose this book in its entirety as understandably as I could, dividing it into fifteen chapters. Almost everything which I have introduced I have displayed with exact proof, in order that those further seeking this knowledge, with its pre-eminent method, might be instructed, and further, in order that the Latin people might not be discovered to be without it, as they have been up to now. If I have perchance omitted anything more or less proper or necessary, I beg indulgence, since there is no one who is blameless and utterly provident in all things. The nine Indian figures are: 9 8 7 6 5 4 3 2 1. With these nine figures, and with the sign 0 ... any number may be written.
Here Leonardo of Pisa uses the word sign "0", indicating it is like a sign to do operations like addition or multiplication, but he did not recognize zero as a number in its own right. From the 13th century, manuals on calculation (adding, multiplying, extracting roots, etc.) became common in Europe where they were called algorimus after the Persian mathematician al-Khwarizmi. The most popular was written by John of Sacrobosco about 1235 and was one of the earliest scientific books to be printed in 1488. Until the late 15th century, Hindu-Arabic numerals seem to have predominated among mathematicians, while merchants preferred to use the Roman numerals. In the 16th century, they became commonly used in Europe.
In mathematics
Elementary algebra
The number 0 is the least non-negative integer. The natural number following 0 is 1 and no natural number precedes 0. The number 0 may or may not be considered a natural number, but it is a whole number and hence a rational number and a real number (as well as an algebraic number and a complex number).
The number 0 is neither positive nor negative, neither a prime number nor a composite number, nor is it a unit. It is, however, even (see evenness of zero).
The following are some basic (elementary) rules for dealing with the number 0. These rules apply for any real or complex number x, unless otherwise stated.
- Addition: x + 0 = 0 + x = x. That is, 0 is an identity element (or neutral element) with respect to addition.
- Subtraction: x − 0 = x and 0 − x = − x.
- Multiplication: x · 0 = 0 · x = 0.
- Division: /x = 0, for nonzero x. But /0 is undefined, because 0 has no multiplicative inverse, a consequence of the previous rule; see division by zero. In the real numbers, for positive x, as y in /y approaches 0 from the positive side, the quotient increases indefinitely toward positive infinity, but as y approaches 0 from the negative side, the quotient tends toward negative infinity.
- Exponentiation: x = 1, except that the case x = 0 may be left undefined in some contexts; see Zero to the zero power. For all positive real x, 0 = 0.
The expression /0, which may be obtained in an attempt to determine the limit of an expression of the form /g(x) as a result of applying the lim operator independently to both operands of the fraction, is a so-called "indeterminate form". That does not simply mean that the limit sought is necessarily undefined; rather, it means that the limit of /g(x), if it exists, must be found by another method, such as l'Hôpital's rule.
The sum of 0 numbers is 0, and the product of 0 numbers is 1. The factorial 0! evaluates to 1.
Other branches of mathematics
- In set theory, 0 is the cardinality of the empty set: if one does not have any apples, then one has 0 apples. In fact, in certain axiomatic developments of mathematics from set theory, 0 is defined to be the empty set. When this is done, the empty set is the Von Neumann cardinal assignment for a set with no elements, which is the empty set. The cardinality function, applied to the empty set, returns the empty set as a value, thereby assigning it 0 elements.
- Also in set theory, 0 is the least ordinal number, corresponding to the empty set viewed as a well-ordered set.
- In propositional logic, 0 may be used to denote the truth value false.
- In abstract algebra, 0 is commonly used to denote a zero element, which is a neutral element for addition (if defined on the structure under consideration) and an absorbing element for multiplication (if defined).
- In lattice theory, 0 may denote the bottom element of a bounded lattice.
- In category theory, 0 is sometimes used to denote an initial object of a category.
Other uses of zero in mathematics
- A zero of a function f is a point x in the domain of the function such that f(x) = 0. When there are finitely many zeros these are called the roots of the function. See also zero (complex analysis) for zeros of a holomorphic function.
- The zero function (or zero map) on a domain D is the constant function with 0 as its only possible output value, i.e., the function f defined by f(x) = 0 for all x in D. A particular zero function is a zero morphism in category theory; e.g., a zero map is the identity in the additive group of functions. The determinant on non-invertible square matrices is a zero map.
In science
Physics
The value zero plays a special role for many physical quantities. For some quantities, the zero level is naturally distinguished from all other levels, whereas for others it is more or less arbitrarily chosen. For example, on the Kelvin temperature scale, zero is the coldest possible temperature (negative temperatures exist but are not actually colder), whereas on the Celsius scale, zero is arbitrarily defined to be at the freezing point of water. Measuring sound intensity in decibels or phons, the zero level is arbitrarily set at a reference value—for example, at a value for the threshold of hearing. In physics, the zero-point energy is the lowest possible energy that a quantum mechanical physical system may possess and is the energy of the ground state of the system.
Chemistry
Zero has been proposed as the atomic number of the theoretical element tetraneutron. It has been shown that a cluster of four neutrons may be stable enough to be considered an atom in its own right. This would create an element with no protons and no charge on its nucleus.
As early as 1926, Professor Andreas von Antropoff coined the term neutronium for a conjectured form of matter made up of neutrons with no protons, which he placed as the chemical element of atomic number zero at the head of his new version of the periodic table. It was subsequently placed as a noble gas in the middle of several spiral representations of the periodic system for classifying the chemical elements. It is at the centre of the Chemical Galaxy (2005).
In computer science
Numbering from 1 or 0?...
The most common practice throughout human history has been to start counting at one. Nevertheless, in computer science zero is often used as the starting point. For example, in almost all old programming languages, an array starts from 1 by default. As programming languages have developed, it has become more common that an array starts from zero by default, the "first" index in the array being 0. In particular, the popularity of the C programming language in the 1980s has made this approach common.
One advantage of this convention is in the use of modular arithmetic. Every integer is congruent modulo N to one of the numbers 0, 1, 2, ..., N−1, where N ≥ 1. Because of this, many arithmetic concepts (such as hash tables) are more elegantly expressed in code when the array starts at zero.
A second advantage of zero-based array indexes is that this can improve efficiency under certain circumstances. To illustrate, suppose a is the memory address of the first element of an array, and i is the index of the desired element. In this fairly typical scenario, it is quite common to want the address of the desired element. If the index numbers count from 1, the desired address is computed by this expression:
where s is the size of each element. In contrast, if the index numbers count from 0, the expression becomes this:
This simpler expression can be more efficient to compute in certain situations.
Note, however, that a language wishing to index arrays from 1 could simply adopt the convention that every "array address" is represented by ; that is, rather than using the address of the first array element, such a language would use the address of an imaginary element located immediately before the first actual element. The indexing expression for a 1-based index would be the following:
Hence, the efficiency benefit of zero-based indexing is not inherent, but is an artifact of the decision to represent an array by the address of its first element.
A third advantage is that ranges are more elegantly expressed as the half-open interval,
This situation can lead to some confusion in terminology. In a zero-based indexing scheme, the first element is "element number zero"; likewise, the twelfth element is "element number eleven". Therefore, an analogy from the ordinal numbers to the quantity of objects numbered appears; the highest index of n objects will be (n-1) and referred to the n:th element. For this reason, the first element is often referred to as the zeroth element to eliminate any possible doubt (though, strictly speaking, this is unnecessary and arguably incorrect, since the meanings of the ordinal numbers are not ambiguous).
Null value
In databases a field can have a null value. This is equivalent to the field not having a value. For numeric fields it is not the value zero. For text fields this is not blank nor the empty string. The presence of null values leads to three-valued logic. No longer is a condition either true or false, but it can be undetermined. Any computation including a null value delivers a null result. Asking for all records with value 0 or value not equal 0 will not yield all records, since the records with value null are excluded.
Null pointer
A null pointer is a pointer in a computer program that does not point to any object or function. In C, the integer constant 0 is converted into the null pointer at compile time when it appears in a pointer context, and so 0 is a standard way to refer to the null pointer in code. However, the internal representation of the null pointer may be any bit pattern (possibly different values for different data types), and has no particular association with zero.
(Note that on most common architectures, the null pointer is represented internally by the integer 0, so C compilers on such systems perform no actual conversion.)
Negative zero
Main article: −0 (number)In mathematics , both −0 and +0 represent the exact same number, i.e., there is no “negative zero” distinct from zero. In some signed number representations (but not the two's complement representation used to represent integers in most computers today) and most floating point number representations, zero has two distinct representations, one grouping it with the positive numbers and one with the negatives; this latter representation is known as negative zero.
In other fields

- In some countries, dialing 0 on a telephone places a call for operator assistance.
- In Braille, the numeral 0 has the same dot configuration as the letter J.
- DVDs that can be played in any region are sometimes referred to as being "region 0"
- In classical music, 0 is very rarely used as a number for a composition: Anton Bruckner wrote a Symphony No. 0 in D minor and a Symphony No. 00; Alfred Schnittke also wrote a Symphony No. 0.
- Roulette wheels usually feature a "0" space (and sometimes also a "00" space), whose presence is ignored when calculating payoffs (thereby allowing the house to win in the long run).
- A chronological prequel of a series may be numbered as 0.
- In Formula One, if the reigning World Champion no longer competes in Formula One in the year following their victory in the title race, 0 is given to one of the drivers of the team that the reigning champion won the title with. This happened in 1993 and 1994, with Damon Hill driving car 0, due to the reigning World Champion (Nigel Mansell and Alain Prost respectively) not competing in the championship.
- In the educational series Schoolhouse Rock!, the song My Hero, Zero is about the use of zero as a placeholder. The song explains that by appending zeroes to a number, it is multiplied by 10 for each one added. This enables mathematicians to create numbers as large as needed.
Quotations
The importance of the creation of the zero mark can never be exaggerated. This giving to airy nothing, not merely a local habitation and a name, a picture, a symbol, but helpful power, is the characteristic of the Hindu race from whence it sprang. It is like coining the Nirvana into dynamos. No single mathematical creation has been more potent for the general on-go of intelligence and power. G.B. Halsted
Dividing by zero...allows you to prove, mathematically, anything in the universe. You can prove that 1+1=42, and from there you can prove that J. Edgar Hoover is a space alien, that William Shakespeare came from Uzbekistan, or even that the sky is polka-dotted. (See appendix A for a proof that Winston Churchill was a carrot.) Charles Seife, from: Zero: The Biography of a Dangerous Idea
...a profound and important idea which appears so simple to us now that we ignore its true merit. But its very simplicity and the great ease which it lent to all computations put our arithmetic in the first rank of useful inventions. Pierre-Simon Laplace
The point about zero is that we do not need to use it in the operations of daily life. No one goes out to buy zero fish. It is in a way the most civilized of all the cardinals, and its use is only forced on us by the needs of cultivated modes of thought. Alfred North Whitehead
...a fine and wonderful refuge of the divine spirit--almost an amphibian between being and non-being. Gottfried Leibniz
See also
- 0
- Negative and non-negative numbers
- Nothing
- Null
- Number theory
- Peano axioms
- Slashed zero
- Hellenistic zero
- Nullar
- Division by zero
- 00
Notes
- Catherine Soanes, ed. (2001). The Oxford Dictionary, Thesaurus and Wordpower Guide. Maurice Waite, Sara Hawker (2nd edition ed.). New York, United States: Oxford University Press. ISBN 978-0-19-860393-3.
{{cite book}}:|access-date=requires|url=(help);|edition=has extra text (help);|format=requires|url=(help); Check|isbn=value: checksum (help) - Lemma B.2.2, The integer 0 is even and is not odd, in Penner, Robert C. (1999). Discrete Mathematics: Proof Techniques and Mathematical Structures. World Scientific. p. 34. ISBN ISBN 9810240880.
{{cite book}}: Check|isbn=value: invalid character (help) - ^ R. W. Bemer. "Towards standards for handwritten zero and oh: much ado about nothing (and a letter), or a partial dossier on distinguishing between handwritten zero and oh". Communications of the ACM, Volume 10, Issue 8 (August 1967), pp. 513–518.
- ^ Bo Einarsson and Yurij Shokin. Fortran 90 for the Fortran 77 Programmer. Appendix 7: "The historical development of Fortran".
- ^ Georges Ifrah. The Universal History of Numbers: From Prehistory to the Invention of the Computer. Wiley (2000). ISBN 0-471-39340-1.
- Kaplan, Robert. (2000). The Nothing That Is: A Natural History of Zero. Oxford: Oxford University Press.
- Binary Numbers in Ancient India
- Math for Poets and Drummers (pdf, 145KB)
- Zero story 1 Zero story 2
- ^ Bourbaki, page 46
- Britannica Concise Encyclopedia (2007). algebra
- No long count date actually using the number 0 has been found before the 3rd century AD, but since the long count system would make no sense without some placeholder, and since Mesoamerican glyphs do not typically leave empty spaces, these earlier dates are taken as indirect evidence that the concept of 0 already existed at the time.
- Diehl, p. 186
- Robert Temple, The Genius of China, A place for zero; ISBN 1-85375-292-4
- Wáng, Qīngxiáng (1999), Sangi o koeta otoko (The man who exceeded counting rods), Tokyo: Tōyō Shoten, ISBN 4-88595-226-3
- The statement in Chinese, found in Chapter 8 of The Nine Chapters on the Mathematical Art is 正負術曰: 同名相除,異名相益,正無入負之,負無入正之。其異名相除,同名相益,正無入正之,負無入負之。The word 無入 used here, for which zero is the standard translation by mathematical historians, literally means: no entry. The full Chinese text can be found at the Chinese Wikisource, wikisource:zh:九章算術.
- Aryabhatiya of Aryabhata, translated by Walter Eugene Clark.
- Ifrah, Georges (2000), p. 416.
- Feature Column from the AMS
- Ifrah, Georges (2000), p. 400.
- Kaplan, Robert. (2000). The Nothing That Is: A Natural History of Zero. Oxford: Oxford University Press.
- Brahmasputha Siddhanta was translated to English by Henry Thomas Colebrooke in 1817 http://books.google.com/books?id=A3cAAAAAMAAJ&printsec=frontcover&dq=brahmagupta
- Henry Thomas Colebrooke. Algebra with Arithmetic of Brahmagupta and Bhaskara. London 1817.
- Sigler, L., Fibonacci’s Liber Abaci. English translation, Springer, 2003.
- Grimm, R.E., "The Autobiography of Leonardo Pisano", Fibonacci Quarterly 11/1 (February 1973), pp. 99-104.
References
This article is based on material taken from the Free On-line Dictionary of Computing prior to 1 November 2008 and incorporated under the "relicensing" terms of the GFDL, version 1.3 or later.
- Barrow, John D. (2001) The Book of Nothing, Vintage. ISBN 0-09-928845-1.
- Diehl, Richard A. (2004) The Olmecs: America's First Civilization, Thames & Hudson, London.
- Ifrah, Georges (2000) The Universal History of Numbers: From Prehistory to the Invention of the Computer, Wiley. ISBN 0-471-39340-1.
- Kaplan, Robert (2000) The Nothing That Is: A Natural History of Zero, Oxford: Oxford University Press.
- Seife, Charles (2000) Zero: The Biography of a Dangerous Idea, Penguin USA (Paper). ISBN 0-14-029647-6.
- Bourbaki, Nicolas (1998). Elements of the History of Mathematics. Berlin, Heidelberg, and New York: Springer-Verlag. ISBN 3540647678.
External links
- A History of Zero
- Zero Saga
- The Discovery of the Zero
- The History of Algebra
- Why numbering should start at zero by Edsger Dijkstra
- "Zeroes" Song parody
- "My Hero Zero" Educational children's song

 , or "∅" (Unicode character U+2205), representing the
, or "∅" (Unicode character U+2205), representing the  ).
).


 ; that is, rather than using the address of the first array element, such a language would use the address of an imaginary element located immediately before the first actual element. The indexing expression for a 1-based index would be the following:
; that is, rather than using the address of the first array element, such a language would use the address of an imaginary element located immediately before the first actual element. The indexing expression for a 1-based index would be the following:


 , because empty ranges often occur as input to algorithms (which would be tricky to express with the closed interval without resorting to obtuse conventions like
, because empty ranges often occur as input to algorithms (which would be tricky to express with the closed interval without resorting to obtuse conventions like  ). On the other hand, closed intervals occur in mathematics because it is often necessary to calculate the terminating condition (which would be impossible in some cases because the half-open interval isn't always a
). On the other hand, closed intervals occur in mathematics because it is often necessary to calculate the terminating condition (which would be impossible in some cases because the half-open interval isn't always a  , both
, both