This is an old revision of this page, as edited by McSly (talk | contribs) at 01:59, 26 October 2008 (Reverted edits by 71.219.84.182 to last version by Mindmatrix (HG)). The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.
Revision as of 01:59, 26 October 2008 by McSly (talk | contribs) (Reverted edits by 71.219.84.182 to last version by Mindmatrix (HG))(diff) ← Previous revision | Latest revision (diff) | Newer revision → (diff) "Lightspeed" redirects here. For other uses, see Lightspeed (disambiguation). For other uses, see Speed of light (disambiguation).The speed of light in the vacuum of free space is an important physical constant usually denoted by the letter c. It is the speed of all electromagnetic radiation, including visible light, in free space. It is the speed of anything having zero rest mass. The SI metre is defined such that the speed of light in a vacuum is exactly 299,792,458 metres per second. (For the value in km/h and other units, see below.)
The speed of light when it passes through a transparent or translucent material medium, like glass or air, is less than its speed in a vacuum. The ratio of the speed of light in the vacuum to the observed phase velocity is called the refractive index of the medium. See dispersion (optics).
In general relativity c remains an important constant of spacetime; however the concepts of 'distance', 'time', and therefore 'speed' are not always unambiguously defined due to the curvature of spacetime caused by gravitation. When measured locally, light in a vacuum always passes an observer at c.
Overview
| Speed of light in different units | |
|---|---|
| metres per second | 299 792 458 (exact) ≈ 3.00×10 |
| km per hour | ≈ 1.08×10 |
| miles per hour | ≈ 6.71×10 |
| miles per second | ≈ 1.86×10 (186 000) |
| feet per nanosecond | ≈ 1 |
The speed of light in vacuum is now viewed as a fundamental physical constant. This postulate, together with the principle of relativity that all inertial frames are equivalent, forms the basis of Einstein's theory of special relativity.
Experimental evidence has shown that the speed of light is independent of the motion of the source. It has also been confirmed experimentally that the two-way speed of light (for example from a source, to a mirror, and back again) is constant. It is not, however, possible to measure the one-way speed of light (for example from a source to a distant detector) without some convention as to how clocks at the source and receiver should be synchronized. Einstein (who was aware of this fact) postulated that the speed of light should be taken as constant in all cases, one-way and two-way.
An observer moving with respect to a collection of light sources would find that light from the sources ahead would be blueshifted while light from those behind was redshifted.
Use of the symbol 'c' for the speed of light
The symbol 'c' for 'constant' or the Latin celeritas ("swiftness") is generally used for the speed of light. NIST and BIPM practice is to use c0 for the speed of light in vacuum. Occasionally, some writers use c for the speed of light in media other than vacuum. Throughout this article c is used exclusively to denote the speed of light in a vacuum.
In branches of physics in which the speed of light plays an important part, such as in relativity, it is common to use a system of units in which c is 1; thus no symbol for the speed of light is required.
Causality and information transfer
According to the theory of Special relativity, causality would be violated if information could travel faster than c in one reference frame. In some other reference frames, the information would be received before it had been sent, so the "effect" could be observed before the "cause". Such a violation of causality has never been recorded.
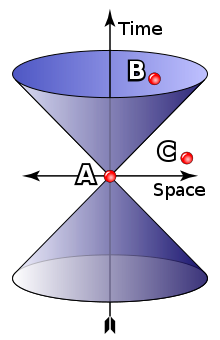
To put it another way, information propagates to and from a point from regions defined by a light cone. The interval AB in the diagram to the right is "time-like" (that is, there is a frame of reference in which event A and event B occur at the same location in space, separated only by their occurring at different times, and if A precedes B in that frame then A precedes B in all frames: there is no frame of reference in which event A and event B occur simultaneously). Thus, it is hypothetically possible for matter (or information) to travel from A to B, so there can be a causal relationship (with A the "cause" and B the "effect").
On the other hand, the interval AC in the diagram to the right is "space-like" (that is, there is a frame of reference in which event A and event C occur simultaneously, separated only in space; see simultaneity). However, there are also frames in which A precedes C (as shown) or in which C precedes A. Barring some way of traveling faster than light, it is not possible for any matter (or information) to travel from A to C or from C to A. Thus there is no causal connection between A and C.
Light years
Astronomical distances are sometimes measured in light-years (the distance that light would travel in one Earth year, roughly 9.46×10 kilometres or about 5.88×10 miles). Because light travels at a large but finite speed, it takes time for light to cover large distances. Thus, the light from distant objects in the universe was emitted from them long ago: in effect, an observer at a large distance sees their distant past. Even light from the sun takes around eight and one-third minutes to reach the earth. If the light from the sun was to cease we would not know about it on Earth for several minutes. Even if an observer close to the sun were to communicate this information to Earth, there would be no way for the communication to warn Earth without violating causality.
Communications and GPS
The speed of light is of relevance to communications. For example, given the equatorial circumference of the Earth is about 40,075 km and c about 300,000 km/s, the theoretical shortest time for a piece of information to travel half the globe along the surface is 0.0668 s.
When light is travelling around the globe in an optical fiber, the actual transit time is longer, in part because the speed of light is slower by about 35% in an optical fiber. depending on its refractive index n, . Furthermore, straight lines rarely occur in global communications situations, and delays are created when the signal passes through an electronic switch or signal regenerator. A typical time as of 2004 for a U.S. to Australia or Japan computer-to-computer ping is 0.18 s. The speed of light additionally affects wireless communications design.
Another consequence of the finite speed of light is that communications between the Earth and spacecraft are not instantaneous. There is a brief delay from the source to the receiver, which becomes more noticeable as distances increase. This delay was significant for communications between ground control and Apollo 8 when it became the first spacecraft to orbit the Moon: for every question, the ground control station had to wait at least three seconds for the answer to arrive. The communications delay between Earth and Mars is almost ten minutes. As a consequence of this, if a robot on the surface of Mars were to encounter a problem, its human controllers would not be aware of it until ten minutes later; it would then take at least a further ten minutes for instructions to travel from Earth to Mars.
This effect forms the basis of the Global Positioning System (GPS) and similar navigation systems. A position on Earth can be determined by means of the delays in radio signals received from a number of satellites, each carrying a very accurate atomic clock, and very carefully synchronized. To work properly, this method requires that (among many other effects) the relative motion of satellite and receiver be taken into effect, which was how (on an interplanetary scale) the finite speed of light was originally discovered (see the following section).
The speed of light can also be of concern over very short distances. In supercomputers, the speed of light imposes a limit on how quickly data can be sent between processors. If a processor operates at 1 GHz, a signal can only travel a maximum of 300 mm in a single cycle. Processors must therefore be placed close to each other to minimize communication latencies, which can cause difficulty with cooling. If clock frequencies continue to increase, the speed of light will eventually become a limiting factor for the internal design of single chips.
Physics
Constant velocity from all inertial reference frames
Most individuals are accustomed to the addition rule of velocities: if two cars approach each other from opposite directions, each traveling at a speed of 50 km/h, relative to the road surface, one expects that each car will measure the other as approaching at a combined speed of 50 + 50 = 100 km/h to a very high degree of accuracy. However, as speeds increase this rule becomes less accurate. Two spaceships approaching each other, each traveling at 90% the speed of light relative to some third observer between them, do not measure each other as approaching at 90% + 90% = 180% the speed of light; instead they each measure the other as approaching at slightly less than 99.5% the speed of light. This last result is given by the Einstein velocity-addition formula:
where and are the (positive) velocities of the spaceships as measured by the third observer, and is the measured velocity of either space ship as observed by the other. This reduces to for sufficiently small values of and (such as those typically encountered in common daily experiences), as the term approaches zero, reducing the denominator to 1.
If one of the velocities for the above formula (or both) are c, the final result is c, as is expected if the speed of light is the same in all reference frames. Another important result is that this formula always returns a value which is less than c whenever v and w are less than c: this shows that no acceleration in any frame of reference can cause one to exceed the speed of light with respect to another observer. Thus c acts as a speed limit for all objects with respect to all other objects in special relativity.
Luminiferous aether (discredited)

Before the advent of special relativity, it was believed that light travels through a medium called the luminiferous aether. Maxwell’s equations predict a given speed of light, in much the same way as is the speed of sound in air. The speed of sound in air is relative to the movement of the air itself, and the speed of sound in air with respect to an observer may be changed if the observer is moving with respect to the air (or vice versa). The speed of light was believed to be relative to a medium of transmission for light that acted as air does for the transmission of sound—the luminiferous aether.
The Michelson–Morley experiment, arguably the most famous and useful failed experiment in the history of physics, was designed to detect the motion of the Earth through the luminiferous aether. It could not find any trace of this kind of motion, suggesting, as a result, that it is impossible to detect one's presumed absolute motion, that is, motion with respect to the hypothesized luminiferous aether. The Michelson–Morley experiment said little about the speed of light relative to the light’s source and observer’s velocity, as both the source and observer in this experiment were traveling at the same velocity together in space.
Interaction with transparent materials
In passing through materials, the observed speed of light can differ from c. The ratio of c to the phase velocity of light in the material is called the refractive index. The speed of light in air is only slightly less than c. Denser media, such as water and glass, can slow light much more, to fractions such as and of c. Through diamond, light is much slower—only about 124,000 kilometres per second, less than of c. This reduction in speed is also responsible for bending of light at an interface between two materials with different indices, a phenomenon known as refraction.
Since the speed of light in a material depends on the refractive index, and the refractive index may depend on the frequency of the light, light at different frequencies can travel at different speeds through the same material. This effect is called dispersion.
Classically, considering electromagnetic radiation to be a wave, the charges of each atom (primarily the electrons) interact with the electric and magnetic fields of the radiation, slowing its progress.
A more complete description of the passage of light through a medium is given by quantum electrodynamics.
Faster-than-light observations and experiments
Main article: Faster-than-light
It is generally considered that it is impossible for any information or matter to travel faster than c, because it would travel backwards in time relative to some observers. However, there are many physical situations in which speeds greater than c are encountered.
Things that can travel faster than c
Wave velocities and synchronized events
It has long been known theoretically that it is possible for the "group velocity" of light to exceed c. One recent experiment made the group velocity of laser beams travel for extremely short distances through caesium atoms at 300 times c. In 2002, at the Université de Moncton, physicist Alain Haché made history by sending pulses at a group velocity of three times light speed over a long distance for the first time, transmitted through a 120-metre cable made from a coaxial photonic crystal. However, it is not possible to use this technique to transfer information faster than c: the velocity of information transfer depends on the front velocity (the speed at which the first rise of a pulse above zero moves forward) and the product of the group velocity and the front velocity is equal to the square of the normal speed of light in the material.
Exceeding the group velocity of light in this manner is comparable to exceeding the speed of sound by arranging people distantly spaced in a line, and asking them all to shout "I'm here!", one after another with short intervals, each one timing it by looking at their own wristwatch so they don't have to wait until they hear the previous person shouting. Another example can be seen when watching ocean waves washing up on shore. With a narrow enough angle between the wave and the shoreline, the breakers travel along the waves' length much faster than the waves' movement inland.
Light spots and shadows
If a laser is swept across a distant object, the spot of light can easily be made to move at a speed greater than c. Similarly, a shadow projected onto a distant object can be made to move faster than c. In neither case does any matter or information travel faster than light.
Quantum mechanics
The speed of light may also appear to be exceeded in some phenomena involving evanescent waves, such as tunnelling. Experiments indicate that the phase velocity and the group velocity of evanescent waves may exceed c; however, it would appear that the front velocity does not exceed c, so, again, it is not possible for information to be transmitted faster than c.
In quantum mechanics, certain quantum effects may be transmitted at speeds greater than c (indeed, action at a distance has long been perceived by some as a problem with quantum mechanics: see EPR paradox, interpretations of quantum mechanics). For example, the quantum states of two particles can be entangled, so the state of one particle fixes the state of the other particle (say, one must have spin +½ and the other must have spin −½). Until the particles are observed, they exist in a superposition of two quantum states, (+½, −½) and (−½, +½). If the particles are separated and one of them is observed to determine its quantum state then the quantum state of the second particle is determined automatically. If, as in some interpretations of quantum mechanics, one presumes that the information about the quantum state is local to one particle, then one must conclude that second particle takes up its quantum state instantaneously, as soon as the first observation is carried out. However, it is impossible to control which quantum state the first particle will take on when it is observed, so no information can be transmitted in this manner. The laws of physics also appear to prevent information from being transferred through more clever ways and this has led to the formulation of rules such as the no-cloning theorem and the no-communication theorem.
Closing speeds
If two objects are travelling towards one another, each at 0.8c as measured in a particular inertial frame of reference, then they are getting closer together at 1.6c as measured in that frame. This is called a closing speed. Note that a closing speed does not represent the speed of any object in an inertial frame; each object is going at 40/41 the speed of light in the other's frame.
Proper speeds
If a spaceship travels to a planet one light year (as measured in the Earth's rest frame) away from Earth at high speed, the time taken to reach that planet could be less than one year as measured by the traveller's clock (although it will always be more than one year as measured by a clock on Earth). The value obtained by dividing the distance travelled, as determined in the Earth's frame, by the time taken, measured by the traveller's clock, is known as a proper speed or a proper velocity. There is no limit on the value of a proper speed as a proper speed does not represent a speed measured in a single inertial frame. Note that a light signal that left the Earth at the same time as the traveller would always get to the destination before the traveller.
Things which only appear to travel faster than c
So-called superluminal motion is seen in certain astronomical objects, such as the jets of radio galaxies and quasars. However, these jets are not moving at speeds in excess of the speed of light: the apparent superluminal motion is a projection effect caused by objects moving near the speed of light and at a small angle to the line of sight.
Travel faster than the speed of light in a medium
Although it may sound paradoxical, it is possible for shock waves to be formed with electromagnetic radiation. As a charged particle travels through an insulating medium, it disrupts the local electromagnetic field in the medium. Electrons in the atoms of the medium will be displaced and polarised by the passing field of the charged particle, and photons are emitted as the electrons in the medium restore themselves to equilibrium after the disruption has passed. (In a conductor, the equilibrium can be restored without emitting a photon.) In normal circumstances, these photons destructively interfere with each other and no radiation is detected. However, if the disruption travels faster than the photons themselves travel, as when a charged particle exceeds the speed of light in that medium, the photons constructively interfere and intensify the observed radiation. The result (analogous to a sonic boom) is known as Čerenkov radiation.
General relativity
Some topics (such as the expansion of the universe, and wormholes) require the application of general relativity and are covered in the main faster than light article.
Other theories concerning the speed of light
Particles that travel faster than light, dubbed tachyons, have been proposed by particle physicists but have yet to be observed. Tachyons, if they existed, would be very different from ordinary particles, and for technical reasons they would not violate the principle of causality.
Some physicists have proposed that the speed of light is different today than it was in the early universe. This theory is called variable speed of light (VSL) and its supporters claim that it explains certain cosmological puzzles. However, it has not gained wide acceptance.
Slow light
Main article: Slow light
Light traveling through a medium other than a vacuum travels below c as a result of the time lag between the polarization response of the medium and the incident light. However, certain materials have an exceptionally high group index and a correspondingly low group velocity. In 1999, a team of scientists led by Lene Hau were able to slow the speed of a light pulse to about 17 metres per second; in 2001, they were able to momentarily stop a beam.
In 2003, Mikhail Lukin, with scientists at Harvard University and the Lebedev Institute in Moscow, succeeded in completely halting light by directing it into a Bose–Einstein condensate of the element rubidium, the atoms of which, in Lukin's words, behaved "like tiny mirrors" due to an interference pattern in two "control" beams.
History
Until relatively recent times, the speed of light was largely a matter of conjecture. Empedocles maintained that light was something in motion, and therefore there had to be some time elapsed in travelling. Aristotle said that, on the contrary, "light is due to the presence of something, but it is not a movement". Furthermore, if light had a finite speed, it would have to be very great; Aristotle asserted "the strain upon our powers of belief is too great" to believe this.
Euclid proposed the emission theory of vision, (also advanced by Ptolemy) where light was emitted from the eye, instead of entering the eye from another source. Using this theory, Heron of Alexandria advanced the argument that the speed of light must be infinite, since distant objects such as stars appear immediately upon opening the eyes.
Medieval and early modern theories
Early Muslim philosophers initially agreed with the Aristotelian view of the speed of light being infinite. In 1021, however, the Iraqi physicist, Ibn al-Haytham (Alhazen), published the Book of Optics, in which he used experiments to support the intromission theory of vision, where light moves from an object into the eye, making use of instruments such as the camera obscura. This led to Alhazen proposing that light must therefore have a finite speed, and that the speed of light is variable, with its speed decreasing in denser bodies. He argued that light is a “substantial matter”, the propagation of which requires time “even if this is hidden to our senses”. This debate continued in Europe and the Middle East throughout the Middle Ages.
In the 11th century, Abū Rayhān al-Bīrūnī agreed that light has a finite speed and observed that the speed of light is much faster than the speed of sound. In the 1270s, Witelo considered the possibility of light travelling at infinite speed in a vacuum but slowing down in denser bodies. A comment on a verse in the Rigveda by the 14th century Indian scholar Sayana may be interpreted as suggesting an estimate for the speed of light that is in good agreement with its actual speed. In 1574, the Ottoman astronomer and physicist Taqi al-Din agreed with Alhazen that the speed of light is constant, but variable in denser bodies, and suggested that it would take a long time for light from the stars which are millions of kilometres away to reach the Earth.
In the early 17th century, Johannes Kepler believed that the speed of light was infinite since empty space presents no obstacle to it. Francis Bacon argued that the speed of light was not necessarily infinite, since something can travel too fast to be perceived. René Descartes argued that if the speed of light were finite, the Sun, Earth, and Moon would be noticeably out of alignment during a lunar eclipse. Since such misalignment had not been observed, Descartes concluded the speed of light was infinite. Descartes speculated that if the speed of light was found to be finite, his whole system of philosophy might be demolished.
Measurement of the speed of light
Early attempts
Isaac Beeckman proposed an experiment (1629) in which a person would observe the flash of a cannon reflecting off a mirror about one mile away. Galileo Galilei proposed an experiment (1638), with an apparent claim to having performed it some years earlier, to measure the speed of light by observing the delay between uncovering a lantern and its perception some distance away. He concluded that the speed of light is ten times faster than the speed of sound (in reality, light is around a million times faster than sound). This experiment was carried out by the Accademia del Cimento of Florence in 1667, with the lanterns separated by about one mile. No delay was observed. Robert Hooke explained the negative results as Galileo had by pointing out that such observations did not establish the infinite speed of light, but only that the speed must be very great.
Astronomical techniques

The first quantitative estimate of the speed of light was made in 1676 by Ole Christensen Rømer, who was studying the motions of Jupiter's moon, Io, with a telescope. It is possible to time the orbital revolution of Io because it enters and exits Jupiter's shadow at regular intervals (at C or D). Rømer observed that Io revolved around Jupiter once every 42.5 hours when Earth was closest to Jupiter (at H). He also observed that, as Earth and Jupiter moved apart (as from L to K), Io's exit from the shadow would begin progressively later than predicted. It was clear that these exit "signals" took longer to reach Earth, as Earth and Jupiter moved further apart. This was as a result of the extra time it took for light to cross the extra distance between the planets, time which had accumulated in the interval between one signal and the next. The opposite is the case when they are approaching (as from F to G). Rømer observed 40 orbits of Io when Earth was approaching Jupiter to be 22 minutes shorter than 40 orbits of Io when Earth was moving away from Jupiter. On the basis of those observations, Rømer concluded that it took light 22 minutes to cross the distance the Earth traversed in 80 orbits of Io. That corresponds to a ratio between the speed of light of the speed with which Earth orbits the sun of 80·42.5 hours⁄22 minutes ≈ 9,300. In comparison the modern value is circa 299,792 km/s⁄29.8 km/s ≈ 10,100.
Around the same time, the astronomical unit was estimated to be about 140 million kilometres. The astronomical unit and Rømer's time estimate were combined by Christiaan Huygens, who estimated the speed of light to be 1,000 Earth diameters per minute, based on having misinterpreted Rømer's value of 22 minutes to mean the time it would take light to cross the diameter of the orbit of the Earth. This is about 220,000 kilometres per second (136,000 miles per second), 26% lower than the currently accepted value, but still very much faster than any physical phenomenon then known.
Isaac Newton also accepted the finite speed. In his 1704 book Opticks he reports the value of 16.6 Earth diameters per second (210,000 kilometres per second, 30% less than the actual value), which it seems he inferred for himself (whether from Rømer's data, or otherwise, is not known). The same effect was subsequently observed by Rømer for a "spot" rotating with the surface of Jupiter. And later observations also showed the effect with the three other Galilean moons, where it was more difficult to observe, thus laying to rest some further objections that had been raised.
Even if, by these observations, the finite speed of light may not have been established to everyone's satisfaction (notably Jean-Dominique Cassini's), after the observations of James Bradley (1728), the hypothesis of infinite speed was considered discredited. Bradley deduced that starlight falling on the Earth should appear to come from a slight angle, which could be calculated by comparing the speed of the Earth in its orbit to the speed of light. This "aberration of light", as it is called, was observed to be about 1/200 of a degree. Bradley calculated the speed of light as about 298,000 kilometres per second (185,000 miles per second). This is only slightly less than the currently accepted value (less than one percent). The aberration effect has been studied extensively over the succeeding centuries, notably by Friedrich Georg Wilhelm Struve and de:Magnus Nyrén.

Earth-bound techniques
The first successful measurement of the speed of light using an earthbound apparatus was carried out by Hippolyte Fizeau in 1849. (This measures the speed of light in air, which is slower than the speed of light in vacuum by a factor of the refractive index of air, about 1.0003.) Fizeau's experiment was conceptually similar to those proposed by Beeckman and Galileo. A beam of light was directed at a mirror several thousand metres away. On the way from the source to the mirror, the beam passed through a rotating cog wheel. At a certain rate of rotation, the beam could pass through one gap on the way out and another on the way back. If is the angle between two consecutive openings and the distance between the toothed wheel and the mirror, then the tooth wheel must rotate with the angular speed:
in order for the light to pass through.Fizeau chose
But at slightly higher or lower rates, the beam would strike a tooth and not pass through the wheel. Knowing the distance to the mirror, the number of teeth on the wheel, and the rate of rotation, the speed of light could be calculated. Fizeau reported the speed of light as 313,000 kilometres per second. Fizeau's method was later refined by Marie Alfred Cornu (1872) and Joseph Perrotin (1900).
Leon Foucault improved on Fizeau's method by replacing the cogwheel with a rotating mirror. Foucault's estimate, published in 1862, was 298,000 kilometres per second. Foucault's method was also used by Simon Newcomb and Albert A. Michelson. Michelson began his lengthy career by replicating and improving on Foucault's method.If is the angle between the normals to two consecutive facets and the distance between the light source and the mirror, then the mirror must rotate with the angular speed:
in order for the light to pass through.
In 1926, Michelson used a rotating prism to measure the time it took light to make a round trip from Mount Wilson to Mount San Antonio in California, a distance of about 22 miles (36 km) each way. The precise measurements yielded a speed of 186,285 miles per second (299,796 kilometres per second).
Laboratory-based methods
During World War II, the development of the cavity resonance wavemeter for use in radar, together with precision timing methods, opened the way to laboratory-based measurements of the speed of light. In 1946, Louis Essen in collaboration with A.C. Gordon-Smith used a microwave cavity of precisely known dimensions to establish the frequency for a variety of normal modes of microwaves—which, in common with all electromagnetic radiation, travels at the speed of light in vacuum. As the wavelength of the modes was known from the geometry of the cavity and from electromagnetic theory, knowledge of the associated frequencies enabled a calculation of the speed of light. Their result, 299,792±3 km/s, was substantially greater than those found by optical techniques, and prompted much controversy. However, by 1950 repeated measurements by Essen established a result of 299,792.5±1 km/s; this became the value adopted by the 12th General Assembly of the Radio-Scientific Union in 1957. Most subsequent measurements have been consistent with this value.
With modern electronics (and most particularly the availability of oscilloscopes with time resolutions in the sub-nanosecond regime) the speed of light can now be directly measured by timing the delay of a light pulse from a laser or a LED in reflecting from a mirror, and this kind of experiment is now routine in undergraduate physics laboratories.
Speed of light set by definition
In 1983, the 17th Conférence Générale des Poids et Mesures defined the metre in terms of the distance traveled by light in a given amount of time, which amounts to adopting a standard value for the speed of light in vacuum:
The metre is the length of the path travelled by light in vacuum during a time interval of 1/299 792 458 of a second.
Here, the term vacuum is meant in the technical sense of free space. This definition of the metre relies on the definition of the second, which is:
The second is the duration of 9 192 631 770 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the caesium 133 atom.
The consequence of this definition is that no experimental measurement could ever change the fact that the speed of light is exactly 299 792 458 metres per second. A precise experimental measurement of the speed of light could, however, refine or alter the length of a metre.
Special relativity
After the work of James Clerk Maxwell, it was believed that light travelled at a constant speed relative to the "luminiferous aether", the medium that was then thought to be necessary for the transmission of light. This speed was determined by the aether and its permittivity and permeability.
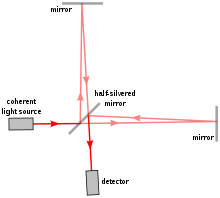
In 1887, the physicists Albert Michelson and Edward Morley performed the influential Michelson-Morley experiment to measure the velocity of the Earth through the aether. As shown in the diagram of a Michelson interferometer, a half-silvered mirror was used to split a beam of monochromatic light into two beams traveling at right angles to one another. After leaving the splitter, each beam was reflected back and forth between mirrors several times (the same number for each beam to give a long but equal path length; the actual Michelson-Morley experiment used more mirrors than shown) then recombined to produce a pattern of constructive and destructive interference. Any slight change in speed of light along one arm of the interferometer compared with its speed along the other arm (because the apparatus was moving with the Earth through the proposed "aether") would then be observed as a change in the pattern of interference. In the event, the experiment gave a null result.
Ernst Mach was among the first physicists to suggest that the experiment amounted to a disproof of the aether theory. Developments in theoretical physics had already begun to provide an alternative theory, Fitzgerald-Lorentz contraction, which explained the null result of the experiment.
It is uncertain whether Albert Einstein knew the results of the Michelson-Morley experiment, but the null result of the experiment greatly assisted the acceptance of his theory of relativity. The constant speed of light is one of the fundamental Postulates (together with causality and the equivalence of inertial frames) of special relativity.
See also
- Čerenkov radiation
- Electromagnetic wave equation
- Faster-than-light
- Free space
- Fundamental Speed
- Mathematical descriptions of the electromagnetic field
- Maxwell's equations
- Metre
- SI units
- Sinusoidal plane-wave solutions of the electromagnetic wave equation
- Speed of sound
- Vacuum
References
Footnotes
- NIST and BIPM practice is to use c0 for the speed of light in vacuum in accord with international standard ISO 31-5. See NIST Special Publication 330, Appendix 2, p. 45 : "Current practice is to use c0 to denote the speed of light in vacuum (ISO 31)." However older publications use just c and many physicists may continue to do this in cases where there is no ambiguity.
- Tai L. Chow (2006). Electromagnetic theory. Sudbury MA: Jones and Bartlett. p. 391-392. ISBN 0-7637-3827-1.
- ^ BIPM. "Unit of length (metre)". SI brochure, Section 2.1.1.1. BIPM. Retrieved 2007-11-28. Or, see: NIST. "Speed of light from direct frequency and wavelength measurements" (PDF). Retrieved 2008-10-17.
- P Beckman and P Mandies Radio. Sci 69D (1965) 623
- Kennedy, Roy J.; Thorndike, Edward M. (1932). "Experimental Establishment of the Relativity of Time". Physical Review. 42 (3): 400–418. doi:10.1103/PhysRev.42.400.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - Hils, Dieter; Hall, J. L. (1990). "Improved Kennedy-Thorndike experiment to test special relativity". Physical Review Letters. 64 (15): 1697–1700. doi:10.1103/PhysRevLett.64.1697.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - Zhang and Chang (1998:171).
- Gibbs, Philip (2004). "Why is c the symbol for the speed of light?". University of California, Riverside. Retrieved 2008-08-20.
- Zhang and Chang (1998:31).
- For multimode and single mode step index fibers operating at wavelengths near 850 nm a typical cladding would have a refractive index of 1.518 and the doped core would have a refractive index of 1.538 which is 1.3% greater. John E. Midwinter (1979). Optical Fibers for Transmission. New York: John Wiley & Sons.
- Current practice is to use c0 to denote the speed of light in vacuum ISO 31. In the original Recommendation of 1983, the symbol c was used for this purpose.
- Francis Weston Sears, Introduction to the Theory of Relativity, p. 24, footnote:
Except in giving a name to , the term "velocity" is used in this book to mean the speed and direction of motion. Velocity is a vector quantity, whereas speed refers only to the magnitude of the velocity. Since we have restricted motion to a single dimension (along the x-axis), we have not needed to introduce the concept of velocity here.
- Physics Department (1998-03-20). "Refraction, Snell's law, and total internal reflection". Boston University. Retrieved 2008-08-20.
- Taylor, Edwin F. (1992), Spacetime Physics, W. H. Freeman, pp. 74–5, ISBN 0716723271
{{citation}}:|first2=missing|last2=(help) - Egan, Greg (2000-08-17). "Applets Gallery / Subluminal". Retrieved 2007-02-06.
References LJ Wang (2000). "Gain-assisted superluminal light propagation". Nature. 406 (406): p277. doi:10.1038/35018520.{{cite journal}}:|pages=has extra text (help); Unknown parameter|coauthors=ignored (|author=suggested) (help) - Electrical pulses break light speed record, physicsweb, January 22, 2002; see also Haché, Alain (2002). "Long-range superluminal pulse propagation in a coaxial photonic crystal". Appl. Phys. Lett. 80: 518. doi:10.1063/1.1432760.
{{cite journal}}: Cite has empty unknown parameter:|month=(help); Unknown parameter|coauthors=ignored (|author=suggested) (help) - Gibbs, Philip (1998). "Shadows and Light Spots". Is Faster-Than-Light Travel or Communication Possible?. University of California, Riverside. Retrieved 2008-08-20.
- Gibbs, Philip (1998). "Third Party Observers". Is Faster-Than-Light Travel or Communication Possible?. University of California, Riverside. Retrieved 2008-08-20.
- M. Rees (1966). "The Appearance of Relativistically Expanding Radio Sources". Nature. 211: 468. doi:10.1038/211468a0.
- Cerenkov, P.A., "Visible Emission of Clean Liquids by Action of γ Radiation", Doklady Akad. Nauk SSSR 2 (1934) 451. Reprinted in Selected Papers of Soviet Physicists, Usp. Fiz. Nauk 93 (1967) 385. V sbornike: Pavel Alekseyevich Čerenkov: Chelovek i Otkrytie pod redaktsiej A. N. Gorbunova i E. P. Čerenkovoj, M.,"Nauka, 1999, s. 149-153. (ref)
- This theory has most notably been advocated by João Magueijo and John Moffat. For an introduction, see for example the article "A time varying speed of light as a solution to cosmological puzzles". For further references see the article Variable speed of light
- L.V. Hau, S.E. Harris, Z. Dutton, and C.H. Behroozi (1999-02-18). "Light speed reduction to 17 metres per second in an ultracold atomic gas" (HTML). Nature. 397: 594–598. doi:10.1038/17561.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - C. Liu, Z. Dutton, C.H. Behroozi, and L.V. Hau (2001-01-25). "Observation of coherent optical information storage in an atomic medium using halted light pulses" (PDF). Nature. 409: 490–493. doi:10.1038/35054017.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - M. Bajcsy1, A.S. Zibrov, and M.D. Lukin (2003-12-11). "Stationary pulses of light in an atomic medium". Nature. 426: 638–641. doi:10.1038/nature02176.
{{cite journal}}: CS1 maint: multiple names: authors list (link) CS1 maint: numeric names: authors list (link) - Bradley Steffens (2006), Ibn al-Haytham: First Scientist, Chapter Five, Morgan Reynolds Publishing, ISBN 1599350246
- Sami Hamarneh (March 1972), "Review: Hakim Mohammed Said, Ibn al-Haitham", Isis 63 (1): 119
- MacKay, R. J.; Oldford, R. W. (August 2000), "Scientific Method, Statistical Method and the Speed of Light", Statistical Science, 15 (3): 254–78, doi:10.1214/ss/1009212817
- ^ Lester, Paul Martin (2005), Visual Communication: Images With Messages, Thomson Wadsworth, p. 10, ISBN 0534637205
- O'Connor, John J.; Robertson, Edmund F., "Abu Ali al-Hasan ibn al-Haytham", MacTutor History of Mathematics Archive, University of St Andrews
- Lauginie, Pierre (2005). "Measuring: Why? How? What?" (PDF). Eighth International History, Philosophy, Sociology & Science Teaching Conference. Retrieved 2008-07-18.
{{cite web}}: Unknown parameter|month=ignored (help) - O'Connor, John J.; Robertson, Edmund F., "Abu Arrayhan Muhammad ibn Ahmad al-Biruni", MacTutor History of Mathematics Archive, University of St Andrews
- Marshall, Peter (1981). "Nicole Oresme on the Nature, Reflection, and Speed of Light". Isis. 72 (3): 357-374 .
{{cite journal}}: Unknown parameter|month=ignored (help) - Sayana-commentary on Rigveda 1.50, see: Müller, Max (ed.): Rig-Veda-Samhita, together with the Commentary of Sayana. Oxford University Press, London (1890).
- Topdemir, Hüseyin Gazi (1999), Takîyüddîn'in Optik Kitabi, Ministry of Culture Press, Ankara (cf. Dr. Hüseyin Gazi Topdemir (June 30, 2008). "Taqi al-Din ibn Ma'ruf and the Science of Optics: The Nature of Light and the Mechanism of Vision". FSTC Limited. Retrieved 2008-07-04.)
- "Historical Background, footnote 5". Statistics and Actuarial Science, University of Waterloo. Retrieved 2007-08-03.
- Lester, Paul Martin (2005), Visual Communication: Images With Messages, Thomson Wadsworth, pp. 10–1, ISBN 0534637205
- Teuber, Jan (2004) "Ole Rømer og den bevægede Jord – en dansk førsteplads?" Template:Da icon in Friedrichsen, Per; Henningsen, Ole; Olsen, Olaf; Thykier, Claus; Tortzen, Chr. Gorm (eds.) Ole Rømer – videnskabsmand og samfundstjener. Kroppedal, Studier i astronomi, Nyere tid, Arkæologi. Gads Forlag, pp. 217–18. ISBN 87-12-04139-4
- Teuber, p. 218.
- Teuber, pp. 218–19.
- J. Cooke, M. Martin, . McCartney and H. Wilf, “Direct determination of the speed of light as a general physics laboratory experiment”, American Journal of Physics, Volume 36, p. 847 (1968). See also Ulabe and Hauk, Proc. of the IEEE
- Kenichiro Aoki� and Takahisa Mitsui, "A small tabletop experiment for a direct measurement of the speed of light," available from ArXiv (3/20/2008)
- Mary B. James, Robert B. Ormond, and Aric J. Stasch, "Speed of light measurement for the myriad," American Journal of Physics, Volume 67, Issue 8, August 1999 pp. 681-684, doi:10.1119/1.19352 Available from AIP (3/20/2008)
- BIPM. "Unit of time (second)". SI brochure, Section 2.1.1.1. BIPM. Retrieved 2008-01-30.
- This definition is subject to a note: This definition refers to a caesium atom at rest at a temperature of 0 K. This note was intended to make it clear that the definition of the SI second is based on a caesium atom unperturbed by black body radiation, that is, in an environment whose thermodynamic temperature is 0 K.
Historical references
- Ole Rømer. "Démonstration touchant le mouvement de la lumière", Journal des sçavans, 7 Décembre 1676, pp. 223–236. Translated as "A Demonstration concerning the Motion of Light", Philosophical Transactions of the Royal Society no. 136, pp. 893–894; June 25, 1677. (Rømer's 1676 paper, in English and French, as bitmap images, and in French as plain text)
- Edmund Halley. "Monsieur Cassini, his New and Exact Tables for the Eclipses of the First Satellite of Jupiter, reduced to the Julian Stile and Meridian of London", Philosophical Transactions XVIII, No. 214, pp 237–256, Nov.–Dec., 1694.
- H.L. Fizeau. "Sur une expérience relative à la vitesse de propagation de la lumière", Comptes Rendus 29, 90–92, 132, 1849.
- J.L. Foucault. "Détermination expérimentale de la vitesse de la lumière: parallaxe du Soleil", Comptes Rendus 55, 501–503, 792–796, 1862.
- A.A. Michelson. "Experimental Determination of the Velocity of Light", Proceedings of the American Association for the Advancement of Science 27, 71–77, 1878. (Project Gutenberg Etext version)
- Simon Newcomb. "The Velocity of Light", Nature, pp 29–32, May 13, 1886.
- Joseph Perrotin. "Sur la vitesse de la lumière", Comptes Rendus 131, 731–734, 1900.
- A.A. Michelson, F.G. Pease, and F. Pearson. "Measurement Of The Velocity Of Light In A Partial Vacuum", Astrophysical Journal 82, 26–61, 1935.
Modern references
- Léon Brillouin. Wave propagation and group velocity. Academic Press Inc., 1960.
- John David Jackson. Classical electrodynamics. John Wiley & Sons, 2nd edition, 1975; 3rd edition, 1998. ISBN 0-471-30932-X
- R.J. MacKay and R.W. Oldford. "Scientific Method, Statistical Method and the Speed of Light", Statistical Science 15(3):254–278, 2000.
- Gerd Keiser. Optical Fiber Communications, pp 32.Mcgraw-Hill, 3rd edition, 2000. ISBN 0072321016.
- Subhash Kak, Template:PDFlink, Annals of the Bhandarkar Oriental Research Institute 80 (1999) 113–123.
- Subhash C. Kak, Template:PDFlink, Indian Journal of the History of Science 33 (1998).
- Zhang, Yuan Zhong; Chang, Yuan-Chung (1998). Special Relativity and Its Experimental Foundations. World Scientific Publishing Company Inc. ISBN 9810227493.
{{cite book}}: CS1 maint: multiple names: authors list (link)
External links
- Speed of light in vacuum (at NIST)
- Definition of the metre (BIPM)
- Data Gallery: Michelson Speed of Light (Univariate Location Estimation) (download data gathered by A.A. Michelson)
- Switching light on and off (news article on stopping light)
- Beam smashes light barrier (news article on group velocity experiment)
- Subluminal (Java applet demonstrating group velocity information limits)
- De Mora Luminis at MathPages
- Light discussion on adding velocities
- Speed of Light (University of Colorado Department of Physics)
- How would we know if the speed of light was varying with time?
- How is the speed of light measured?
- The Fizeau "Rapidly Rotating Toothed Wheel" Method
| Extremes of motion | |
|---|---|
| Speed | |
| Distance | |
| Endurance | |
| See also | |
Template:Link FA Template:Link FA Template:Link FA
Categories: . Furthermore, straight lines rarely occur in global communications situations, and delays are created when the signal passes through an electronic switch or signal regenerator. A typical time as of 2004 for a U.S. to Australia or Japan computer-to-computer
. Furthermore, straight lines rarely occur in global communications situations, and delays are created when the signal passes through an electronic switch or signal regenerator. A typical time as of 2004 for a U.S. to Australia or Japan computer-to-computer 
 and
and  are the (positive) velocities of the spaceships as measured by the third observer, and
are the (positive) velocities of the spaceships as measured by the third observer, and  is the measured velocity of either space ship as observed by the other. This reduces to
is the measured velocity of either space ship as observed by the other. This reduces to  for sufficiently small values of
for sufficiently small values of  approaches zero, reducing the denominator to 1.
approaches zero, reducing the denominator to 1.
 and
and  of c. Through diamond, light is much slower—only about 124,000 kilometres per second, less than
of c. Through diamond, light is much slower—only about 124,000 kilometres per second, less than  is the angle between two consecutive openings and
is the angle between two consecutive openings and  the distance between the toothed wheel and the mirror, then the tooth wheel must rotate with the angular speed:
the distance between the toothed wheel and the mirror, then the tooth wheel must rotate with the angular speed:


 the distance between the light source and the mirror, then the mirror must rotate with the angular speed:
the distance between the light source and the mirror, then the mirror must rotate with the angular speed: