This is an old revision of this page, as edited by Datumizer (talk | contribs) at 01:07, 8 February 2010 (→Break: ask for another third opinion). The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.
Revision as of 01:07, 8 February 2010 by Datumizer (talk | contribs) (→Break: ask for another third opinion)(diff) ← Previous revision | Latest revision (diff) | Newer revision → (diff)| Color B‑class High‑importance | ||||||||||
| ||||||||||
| HSV color space has had a peer review by Misplaced Pages editors which is now archived. It may contain ideas you can use to improve this article. |
|
Archives |
|
HSL vs. HSI
HSI is different than HLS. HLS is sometimes known as HSL, not HSI. HSI is a cylindrical model, where H (hue) is an angle from 0 through 360 degrees, S (saturation) is the distance from the origin around which H rotates (normalized to range from 0 through 1), and I is intensity, which is distance along the vertical axis of the cylinder (again, ranging from 0 through 1). HSV (hue, saturation, value) and HSB (hue, saturation, brightness) are the same as each other, but are not the same as HLS. See Digital Image Processing by Kenneth R. Castleman, chapter 21, for a description of the HSI color model. Seaandsky 21:54, 3 October 2007 (UTC)
- Can you give a better description? Maybe make a quick sketch image (or even ascii art would be fine :))? I'm not understanding the difference. --jacobolus (t) 21:46, 4 October 2007 (UTC)
I think the article should not say HLS and HSV are cylindrical. This is not correct. HLS is a double hexcone and HSV is a single hexcone. HSI is a cylinder. I will try to get back with some drawings if I can find any. :) Seaandsky 00:24, 9 October 2007 (UTC)
- Here are some illustrations, but they don't quite align with how you're putting it. Dicklyon 04:45, 9 October 2007 (UTC)
- No, mathematically they both are cylinders. But these can be thought of as simple transformations of cones or hexcones (or I suppose more accurately: topologically, cylinders, hexcones, and cubes are all the same, so HSV can be thought of as any one of the three, but the metric used is most straight-forward on a cylinder). I plan on explaining this more clearly, with pictures, but give me a few days to write the description. --jacobolus (t) 05:07, 9 October 2007 (UTC)
- It's straightforward on a cylinder only if the saturation limit is fixed, independent of the lightness dimension. The other shapes more appropriately describe the saturation limits in different systems. Now if we could only be sure which is which... Dicklyon 05:13, 9 October 2007 (UTC)
- The way it works is that the saturation limit *is* fixed, but a saturation of n is thought of as different “amounts” of saturation depending on the lightness (at least for HSV; s = (max - min) / max, where max = max(r, g, b), etc., so when any of r, g, b is 0, s is 1). Similarly, saturation is defined on a 0-1 scale regardless of hue, and "hue angle" in the "hexcone" is not really angle geometrically, but is rather defined as if each segment of the hexagon was warped into the corresponding arc. This is IMO best explained by showing the transformation from RGB cube to hexcone or double hexcone, and then further showing the transformation from hexcone to cylinder, with pictures. --jacobolus (t) 05:19, 9 October 2007 (UTC)
- It would be great if this could be cleared up in terms of how HSV, HSL, HSB, HLS, etc. work mathematically and have graphical depictions of these as such 'as is', and discussing user-friendly visualizations in appropriate sections. For example, the cylindrical depiction of the HSV method has the description that it "might" be considered the mathematically most accurate depiction - I'd say drop the "might", as it simply is. An alternative depiction is given in the form of the tip-down cone - however this depiction implies that with decreased Value, the Saturation (distance from cone revolution axis to boundary) decreases as well, which in the HSV model referred to in this article (See also Dicklyon's comment for a page which describes there being two models named HSV) is not the case. Similarly, the only depiction given for HSL, "HSL arranged as a double-cone", does not fit the rest of the description nor the RGB to HSL conversion formula given. The article itself states that "a very pastel, almost white color can be defined as fully saturated in HSL". The depiction provided does not fit this claim. Mathematically, both would have to be cylinders to fit their descriptions. The conversion formula seems to fit this notion - a pale RGB color of when fed through the conversion to HSL gives a Saturation of L = (1.0 + 0.9) / 2.0 = 0.95 : S(L>0.5) = (1.0 - 0.9) / (2 - 1.0 + 0.9) = 0.1 / (2 - 1.9) = 0.1 / 0.1 = 1.0 . The 'hexcone' depiction is even worse, in my opinion, as it implies a varying saturation level when going along the hue wheel (e.g. Red = = 1.0, Orange = = 0.866.., Yellow = = 1.0) when measuring distance from the edge to the center axis (Edit: I understand that this is not how Saturation -is- determined within a hexcone, but without explanation that is not immediately clear.). I do understand that there are modifications to the two described in my comment as described in the article (ignoring the depictions) that may in fact fit the depictions and can be very useful; for example, the HSL method depicted (but not described) with a double-cone is superior to the cylindrical HSL when comparing two RGB values within such a space. A nearly-black RGB value RGB in the cylindrical HSL results in the values HSL, which in terms of saturation places it nowhere near a black RGB value RGB = HSL; in fact, bright red RGB = HSL is a closer match within this method. The depicted double-cone HSL method does not suffer from this, to most observers (visual and mathematical), illogical behavior. On the other hand, the cylindrical method is much easier to work with visually and loses less fidelity code-wise (in limited bitdepth systems). I may certainly be entirely mistaken, but my excuse is the conflicting data both within a single article as well as from different sources cited. I look forward to jacobolus' edits and any further brainstorming/source citing/real world implementation conventions (not sure if the conical HSV, which may be the original, is what HSV should be described as, given that all the HSV implementations I'm aware of use a cylindrical HSV) ZeBoxx 00:04, 19 October 2007 (UTC)
- Yes, you're on the right track; you've hit on the essential problem which is that conceptually these models describe a cone or double-cone (or hexcone/double-hexcone), but leave their values mathematically in a (, ) range, which looks like a cylinder, when plotted in any reasonable fashion. I intend to make these distinctions clear (and with better pictures eventually) when I get around to rewriting this article, which I was planning to do sometime last week, but might not happen now for another week at least. --jacobolus (t) 00:47, 19 October 2007 (UTC)
- For those who know German, the following page touches on many of the points made in other comments as well (RGB cube set on a corner, etc.). They, too, conclude that it is frustrating that there are so many conflicting descriptions and depictions - while also noting that for end-users, it hardly matters which model is used and how, as typical color-picking utilities are plenty intuitive no matter which model is chosen. http://www.hrz.uni-dortmund.de/computerPostille/September1999/00.html ZeBoxx 00:36, 19 October 2007 (UTC)
- Heh. Whereas my conclusion (like that of Charles Poynton), is that none of these is particularly useful anymore on modern computer hardware which can quickly compute RGB values for colors in more accurate and intuitive models such as L*u*v*, L*a*b*, etc. --jacobolus (t) 00:51, 19 October 2007 (UTC)
- I think the authors' conclusion is based mostly on the notion that most color pickers are no longer just three numerical fields into which you enter data and out pops a color; which would make HSV fairly confusing indeed ("I desaturated my Red and now it's White - what the.."). But with the typical triangle/square/whatnot presentation on-screen, interactively changing any of the values (or just picking one from right within the chart), no such concerns really exist. Picking a 'yellow' that is perceptually the same brightness as red becomes an issue of how good the user's vision is (L*a*b* won't save a colorblind person) and picking the color rather than one of endlessly fiddling with numerical values. That said, CIE L*a*b* does tend to be a superior color space for most perceptually-important operations (there's a reason color likeness functions, from plain delta E all the way to the behemoth that is CIEDE2000, base themselves off of it), but I wouldn't go as far as Poynton to say that HSV/HSB/HSL/etc. should be abandoned altogether; the single parameter Hue alone sets them aside enough from any of the other color models to be indispensable. The many variations is just a little (understatement) overkill, however ZeBoxx 06:51, 19 October 2007 (UTC)
- You've obviously never tried using a more perceptually-uniform/intuitive color picker, in comparison to an HSV/HSL one. ;) --jacobolus (t) 13:08, 19 October 2007 (UTC)
- I've had to work with the strangest colorpickers (from RGB straight up to a LogLuv one for HDR colorpicking, they all have their pros and cons. HSV/etc. aren't so bad, as long as you get the visual charts to go with them so that you can see what does what; that was the point.. the colorspace/model doesn't matter so much in colorpickers as you get direct feedback/etc. anyway.. yes, RGB will still be more intuitive than, say, CMYK when working on a computer - but anybody who's only used to RGB can happily work with a colorpicker set to CMYK. Offer then only four value controls, one for each channel, and no graphical feedback, though, and they're far more likely to get stuck. In that sense, I don't think the colorspace/model matters too much for the purpose of colorpickers. For purposes of matching colors in any standard way, finding complementary colors, storage accuracy etc. - that's where the spaces/models are a more important element. ZeBoxx 01:29, 20 October 2007 (UTC)
- I've been waiting to see the updated page before I made any more comments, but I do hope it will come soon because at the moment it may be a little unintentionally misleading. It's important to interpret saturation in the equations for conical HSV and HLS in terms of something along the lines of a percentage of the maximum for the particular value or lightness. Saturation of 1 means the color is on the surface of the cone. However, the distance between the surface of the cone and the vertical axis varies as value or lightness increases or decreases (for a cone, but not for a cylinder). So a saturation of 0.6 at one lightness is further away or closer to the vertical axis than at some other lightness, for the conical models. This is distinctly different than the cylindrical model, in which the saturation can be interpreted literally as a normalized distance from the vertical axis. The equations for each are different and the results are distinctly different when you see them displayed. At lightness = 1 in the double hexcone HLS model, you will see white. However, in a cylindrical model, at lightness = 1, you may still see some hue, depending on the saturation. (Note: you must also pay attention to whether the equations refer to a hexcone or a cone where the surface has been "warped" so that it is round.) Here's a link to some of the more basic equations for HLS, HSV and HSI: http://www5.informatik.tu-muenchen.de/lehre/vorlesungen/graphik/info/csc/COL_23.htm#topic22. I look forward to your updates. Seaandsky 17:03, 19 October 2007 (UTC)
I did not find any better illustrations than those mentioned by Dicklyon above on the web. The book and chapter I mentioned above, by Castleman, has an illustration of cylindrical HSI. Below, you say you are looking for references. There is also a book by Alan Watt, titled 3D Computer Graphics, published by Addison Wesley, which goes into the HLS and HSV color spaces in chapter 14. I do find that on the web, HSV and HLS may sometimes be depicted as hexcones and sometimes are transformed into cylinders (by "warping", as you say, the segments of the hexagon). The hexcones, as you have already said, come from tipping the RGB cube up so that its neutral (black-to-white) diagonal lies along the z-axis. As Dicklyon says, the cylinder then comes about from using a saturation maximum that is fixed, independent of the lightness level. Seaandsky 13:27, 9 October 2007 (UTC)
- Dick sent me a copy (via email) of Alvy Ray Smith's original paper, which explains the geometric intuition behind the models. I was planning to turn his explanation into some diagrams of my own; I don't really find any of the existing diagrams I've found online satisfactory. --jacobolus (t) 13:35, 9 October 2007 (UTC)
Some time later...
I would just like to comment that the particular geometric solid used to depict HSL, HSV, HSI, etc. doesn't really matter. It's a matter of preference, not mathematical accuracy. The models all use three parameters, and they can be applied to any function that also takes three parameters. They can be mapped to a cylinder, sphere, cone, cube, whatever. There's also the hexcone. The use of the sphere in some form or another dates back to at least 1810 (see the image here, the image is described here). For instance, Also, the square color picker can be seen as either a slice (e.g., a partial cross-section) of a cylinder or a cross-section of a cube. The triangular color picker can be seen as a slice of a cone. SharkD (talk) 06:19, 13 January 2008 (UTC)
- I think if you'll look more closely you see how the shape of the solid is important. First of all, I think we all agree that hue has to be arranged in a loop (circle or hexagon); now in HSL white is a unique L=1 top point; that is, when L is 1, S must be 0. This relationship is lost if you distort the space to a cylinder; for a sphere it can still work, perhaps, but it works most naturally with a bi-cone. Both HSL and HSV have a similar point at black. Why would anyone use cylinders for this? Dicklyon (talk) 07:57, 13 January 2008 (UTC)
- That's not the case; luminance and saturation are independant of each other. A color can have any value for saturation; and, as long its luminance is equal to 1, it will be white. Also, this convergance upon a single point affects all the other colors, as well. Simply because the color white can only have one value for saturation—or is only a single color as opposed to a range of colors—doesn't mean it logically follows that all the other colors become less saturated (because of the slope) as they increase in luminance. SharkD (talk) 09:13, 13 January 2008 (UTC)
- Not the case? Are you ignoring the defining equations and/or the limitation on the range of values? Getting L=1 requires min=max=1, so max-min is 0, so S is 0. They are not independent. The HSL model certainly does imply that colors become less saturated as L approaches 1; it's even logical, since L=1 means white, to say that all colors become less saturated as they approach white. That's the HSL model. HSV is different, being a cone, not a bicone. It all comes from the equations. Dicklyon (talk) 09:32, 13 January 2008 (UTC)
- View this simple animation of the saturation changing and the color remaining white. SharkD (talk) 10:22, 13 January 2008 (UTC)
- Yes, that's clear evidence that you are not the only one to ignore the definitions. It makes sense in such an interface to map nonsense coordinates back into real colors, which is why they do it. But does it help clarify the structure of the defined color model? No. Dicklyon (talk) 17:32, 13 January 2008 (UTC)
- The formula I use to convert RGB to HSL sets the Hue to zero instead of "undefined" when min - max = 0. This is an arbitrary value necessary to keep the function from returning a range of values instead of only a single value. The same is true for Saturation when Luminance is equal to 0 or 1. Having the function return an "undefined" value would result in a nonsense RGB value that the computer could not interpret. Setting Hue or Saturation to zero is a necessity to keep computer applications from breaking, not due to mathematical accuracy. SharkD (talk) 19:09, 13 January 2008 (UTC)
- Hue's no problem. The hue angle doesn't affect the geometry when it's at zero radius due to zero saturation. But the Saturation is defined as zero at black and white, not undefined. The shape of the solid is determined by the range of L and S values that you can get from the defined range of R, G, and B values. You can decide how to map L and S to height and radius or latitude or whatever, but no matter how you do it, you'll have something like a bi-cone, with white at the L=1 point where S can not be other than 0, and black at the L=0 point where again S can not be other than 0. You can't get a cylinder out of it. The only thing "undefined" is where the value has no geometric effect; there's no other place that blows up; and converting from HSL to RGB is not the issue; the domain (RGB) determines the range of HSL. Dicklyon (talk) 19:25, 13 January 2008 (UTC)
- How about you do the reverse: use the HSL to RGB conversion formula and experiment with changing the Saturation values while keeping the Luminance 0 or 1. If these experiments lead to the results I describe, is this formula, then, also "wrong"? SharkD (talk) 19:30, 13 January 2008 (UTC)
What needs to be done
SharkD, you have some great 3D image making tools and abilities, but you've not applied them ideally, seems to me. For example, Image:HSL sphere color solid.png still has a misspelling and an incorrect indication of saturation as radius in the sphere; if you want to embed HSL in a sphere, you need to work out a mapping that works, and illustrate it correctly. As for the cylinders, I suggest we get rid of them, and instead illustrate the solid shapes that represent the range of HSL and HSV values that come from applying the definitions to the domain of RGB values. Agree? Other opinions? Dicklyon (talk) 19:36, 13 January 2008 (UTC)
- No, I think the cylinders should stay, as they are the most uniform way of displaying the geometry used by the coordinate systems of the two models. Given the numerical mapping in use by HSL/HSV models, cones and double cones, whether hexagonal or circular, are extremely distorted. In other words, in a cylinder, changing e.g. *l* by 0.5 is a uniform movement, whereas in some other shape, the movement is unnaturally dependent on position in the shape. --jacobolus (t) 19:51, 13 January 2008 (UTC)
- The spherical depiction is just as "uniform" as the cylindrical depiction. A cube is uniform, as well. SharkD (talk) 20:46, 13 January 2008 (UTC)
- That's certainly not true. If you increase s from, say, 0.3 to 0.7, you will always move 0.4 units in a cylindrical mapping. In a spherical mapping, s = 1.0 is defined relative to the edge of the sphere, so at the center (i.e. v = 0.5), you'd be moving 0.4 units, but halfway up (v = 0.75), you'd only be moving 0.4×√3/2 units. It is the complexity of the resulting arithmetic that makes a sphere a particularly inappropriate distortion of HSV: a double-cone or double-hexcone is a more comprehensible geometrical representation. --jacobolus (t) 21:07, 13 January 2008 (UTC)
- I guess I don't understand what Jacobolus is saying about uniformity and the cylinder. Isn't it just height = l, radius from axis = s and angle = h? If so, then it's the same geometry as the cone and bicone, within the range of the defining functions, and an arbitrary filling in of values outside that range. Or is there some other mapping to cylinder coordinates that I've missed or that has not been stated? As to the sphere, I haven't seen a mapping to that, either, except for the one implied by the illustration, which is obviously "wrong" in that it gets the wrong saturation at the poles. Dicklyon (talk) 21:11, 13 January 2008 (UTC)
- Take a closer look at the sphere again. The saturation remains constant for a given distance from the center, not the distance from the central axis. This is a common misunderstanding of lattitude. Lattitude is not a linear movement "up" or "down"—it's a rotation around the center. Imagine if the Earth expanded. The lines of lattitude and longitude would not move up or down linearly. They would scale with the changing radius, which would result in a non-linear vertical transformation. This is clearly evidenced if you take a look at the parametric equation for the sphere. SharkD (talk) 21:29, 13 January 2008 (UTC)
- Right, and that's the problem. It implies that white and black have saturation of 1, while the definitions say the saturation of white and black should be zero. If you measured from the axis, instead of from the center, it would be possible to get those right, whereas with measurement of spherical radius it is not possible. Dicklyon (talk) 22:02, 13 January 2008 (UTC)
- According to the article on the sphere, "In mathematics, a sphere is the set of all points in three-dimensional space (R3) which are at distance r from a fixed point of that space, where r is a positive real number called the radius of the sphere." The parametric formula for the sphere is,
- I simply substituted H, S and L for theta, r and phi. E.g.,
- I see. I mean, is that really what you did? Because it maps both white and black, and all grays for that matter, to the center of the sphere, and leaves other points on the axis undefined, which seems like a peculiar interpretation. If you could map the surface of the cylinder onto the sphere that way, but map the axis of the cylinder directly onto the axis of the sphere without collapsing it to the center point, so that you could preserve a representation of neutrals, that might work a lot better. The simplest way would be to just distort the distance from the axis of the cylinder to make a sphere, rather than starting from the kind of spherical parameterization you used. Dicklyon (talk) 04:17, 14 January 2008 (UTC)
- Yes, this is what I did. You can confirm this by doing the mental math of inputting arbitrary values for H, S and L into the formula, visualizing the results and then comparing them to a reference image (this image is a bit better for the purposes of mental visualization, as individual colors are hard to distinguish apart in the ray-traced image). If you have access to POV-Ray, I could create a demonstration scene which would do a better job of showing this. Other points along the vertical axis are not undefined; they all have their corresponding H, S and L vectors. SharkD (talk) 06:21, 14 January 2008 (UTC)
- I see. I mean, is that really what you did? Because it maps both white and black, and all grays for that matter, to the center of the sphere, and leaves other points on the axis undefined, which seems like a peculiar interpretation. If you could map the surface of the cylinder onto the sphere that way, but map the axis of the cylinder directly onto the axis of the sphere without collapsing it to the center point, so that you could preserve a representation of neutrals, that might work a lot better. The simplest way would be to just distort the distance from the axis of the cylinder to make a sphere, rather than starting from the kind of spherical parameterization you used. Dicklyon (talk) 04:17, 14 January 2008 (UTC)
- OK, I was thinking of L as the height, still, like in the cylinder; I see that with the angle, the only real undefined point is the center, where all the neutrals map. That is, you've got an embedding where when s=0, you don't get to know anything about l. Dicklyon (talk) 06:48, 14 January 2008 (UTC)
- Incidentally, in Phillip Otto Runge's mapping of H, S and L to a sphere (see the image in his biography article), L is the height. I don't understand why he did this. I don't understand the math behind it. SharkD (talk) 07:37, 14 January 2008 (UTC)
- Here is the parametric formula for a cylinder:
- Substituting H, S and L for theta, r and z results in the cylindrical depiction already present in the article.
- Here is the parametric formula for a cone:
- Substituting H, S and L in for theta, r and z results in a cone (but not a double cone).
- Here is the parametric formula for a solid cuboid (the parametric formula for the surface, only, is a bit more complicated, as it requires additional logic):
- Substituting H, S and L in for x, z and y results in this image. SharkD (talk) 03:51, 14 January 2008 (UTC)
- That cuboid doesn't respect the circular nature of hue, which is part of why it looks so bad. Dicklyon (talk) 04:17, 14 January 2008 (UTC)
- Well, strictly speaking, the HSL model doesn't have a circular nature for hue. The values for H, S and L all increase linearly to some limit. The computer doesn't treat one value as especially "circular". Hue exists along a linear spectrum that extends into other wavelengths that can't be considered colors. Users simply find arranging hues into circles to be more "intuitive". I find the spherical depiction doubly "intuitive", as users don't have to switch from thinking along linear lines to circular ones for different parameters. You get whatever benifits there are from "circular" thinking for both parameters. But, this is just a preference. Some users will prefer the cube model. SharkD (talk) 06:44, 14 January 2008 (UTC)
- Well, sure, for the benefit of the digitization, the circle is broken into a principal segment from 0 to 360; but since neighboring colors cross the cut, it's not a good idea to ignore the underlying circular structure. H is the only one that has this circular nature. As to some users maybe preferring that cube, that's hard to imagine, but out of a nearly infinite population of users, I guess anything's possible. Dicklyon (talk) 07:10, 14 January 2008 (UTC)
- As I said, hue doesn't really have a circular nature. A circle is just the preferred method of visualization. SharkD (talk) 07:27, 14 January 2008 (UTC)
- I'm not sure what you mean by "doesn't really have a circular nature". Hue ranges from
- The definition of a circle is all points equidistant from a central point. In physics, there is no "thing" that hues are oriented around. From the color wheel article: "A color wheel or color circle is an organization of color hues around a circle, showing relationships between colors considered to be primary colors, secondary colors, complementary colors, etc." The arrangement of hues around a circle is a human construction, designed for "usability" reasons (e.g., it's useful as a learning aid). It does not occur this way in nature. "In normal human vision, wavelengths of between about 400 nm and 700 nm are represented by this incomplete circle, with the longer wavelengths equating to the red end of the spectrum." Wavelength is a linear measurement of the distance between the peaks of a sinosoidal wave. The value for h can be normalized to any value. Its normalization to 0-360 degrees indicates a preference for a given visualization. SharkD (talk) 19:59, 14 January 2008 (UTC)
- I feel like this discussion is a pedantic semantic quibble, and like I'm talking past you, without making myself understood. I suppose you aren't willing to take my word for it that bright red is equivalent to bright red, and that the “hue” of HSL and HSV has been explicitly set up in the model to “wrap around” from one edge to the other (the topological definition of a circle). I'm not sure if there is anything I can say to convince you, other than suggesting you look again at the construction of HSV from the RGB color cube, where geometrically, this “wrap-around” aspect seems pretty obvious. If you really want to have a philosophical argument about the meaning of “circle”, I suggest you look elsewhere, as a discussion of the topic as it applies to HSL/HSV does not interest me. The article about color vision may help you understand the distinction between wavelength and hue. If you're still hung up about it, I can suggest some books which further explain the subject. --jacobolus (t) 20:44, 14 January 2008 (UTC)
- Here is a nice article that describes how the arrangement of hues into circles was arrived at. It supports my argument that hues aren't arranged into circles based on physical properties of beams of light. Rather, it was designed to make geometric calculations easier—hence "usability". All arrangements of hue into a circle are descended from Newton's circle. Further, the functions provided in this article simply convert one set of vectors into another set of vectors. Though a circular mapping of hue was explicitely intended, as you say, how you map these vectors is really arbitrary. SharkD (talk) 22:26, 14 January 2008 (UTC)
- I'm sorry if my arguments seem to come across as bothersome. I feel hesitant about getting into what is essentially a "popularity contest" about which depiction is most appropriate. SharkD (talk) 22:45, 14 January 2008 (UTC)
- Newton thought there was something physical about closing the 1D wavelength parameter into a hue loop, but he was wrong. The circular nature of hue comes from psychophysics or physiology, not from physics. But it's very real; any kind of colorimetric representation has hue loops surrounding neutrals. You can always break the loop and show it as an open 1D parameter, but that's too much of a bastardization of HSL and HSV, and loses the important representation/topological property that was intended in defining in terms of angles. So let's just not go there; it has nothing to do with popularity. Dicklyon (talk) 23:17, 14 January 2008 (UTC)
- I don't see how it logically follows that there is a circular property simply because some representations arrange hue in a circle. I agree that arranging hue in this fashion is useful for highlighting certain processes that occur within this domain. Also, I'm sure Newton was well aware that his arrangement of hue into a circle was not based on physical properties. SharkD (talk) 23:49, 14 January 2008 (UTC)
- One other nifty thing about the sphere is that lightness and darkness are mapped as polar opposites. It kind of reminds me of this diagram. SharkD (talk) 22:11, 14 January 2008 (UTC)
- As for SharkD's models, I have a few main problems with them: the misspelling is annoying (not to mention that L is not usually taken to stand for “luminance” at all, whatever the spelling; better I think to leave these labeled H, S, L, and V, particularly as S means something different quantitatively for each of the models), the shading applied to them is unfortunate, as it alters the relationship of the colors, and w.r.t. the sphere in particular, it seems quite unsaturated, the horizontal grid is distracting, the vertical axis line probably shouldn't cover the lower half of the sphere, I don't really like the curvature in the lettering, and it's not really a big deal, but I think I'd personally choose a different section to cut away. --jacobolus (t) 19:59, 13 January 2008 (UTC)
- I used "luminance" because it is used in the Windows color picker. I can change this if the usage of the term is inappropriate (I think the article discusses this somewhere), though a Google search doesn't really show a great disparity in the usage of the two terms (hue saturation luminance = 30K+ hits, hue saturation lightness = 40K+ hits). As for the horizontal grid, it places the object within the coordinate system, which is important when trying to model the object (note the difference in position within the coordinate system between the sphere and the cylinder). The vertical axis passes through the bottom of the sphere because one of the lines of longitude passes through the center of the viewing plane. You see through the line of longitude to the other side. SharkD (talk) 20:46, 13 January 2008 (UTC)
- I'm sorry about the mispelling. I will fix this soon. As for mapping Saturation to the radius— what exactly is wrong with this? It is done in the case of both the cone and cylinder depictions. SharkD (talk) 20:46, 13 January 2008 (UTC)
- If you map things to a sphere, saturation is still radius w.r.t. a cylinder, that is, horizontal. The distance from the center of the sphere to a point is meaningless. --jacobolus (t) 21:02, 13 January 2008 (UTC)
- It's really not clear what the right mapping is for a sphere, but distance from the axis will at least go to zero at the poles, unlike distance from the center, which does not. Dicklyon (talk) 21:11, 13 January 2008 (UTC)
OK, I goofed
On reviewing the defining equations for s, I see that I was wrong. Apparently in both HSL and HSV it does have a range out to 1 for all values of L or V, which is what Jacobolus and SharkD have been saying about the space being a cylinder. This is a disconnect from what I thought the definition was. I'll have to review the sources and see if there are different versions, or if I was just remembering wrong. And it makes some of my recent edits wrong, so I'll fix that. Sorry about the confusion. Dicklyon (talk) 21:19, 13 January 2008 (UTC)
- Right, and that is what Alvy Ray Smith's formulae have as well, even though he calls them hexcones. But the geometrical intuition for the model of HSL for example is based on a hexcone created from the RGB color cube, and I want to create some diagrams which better display the progression from color cube → hexcone → cylinder, as I think that will clarify things for readers. --jacobolus (t) 04:31, 14 January 2008 (UTC)
Sphere
I'm responding here after a message on Misplaced Pages talk:WikiProject Mathematics#Help on parametric math. One way to find appropriate solids is to find which values of (h,s,l) give the same colour, ideally these are represented by a single point. In particular white (h,s,1) and black (h,s,0) should map to single points, giving the double-cone shape. From this double cone other shapes can be obtained. By pressing the top point downwards you get a single cone. By expanding the bottom point of this cone to a disk you can get a cylinder, with the base of the cylinder all black.

I'm fairly sure the sphere image is wrong. With that image if saturation is 0 you get the center of the sphere yet changing lumanance should give a range of colours from black to white. Note in the graphic to the right, in the bottom right image that all-points on the lower half of the axis give black. --Salix alba (talk) 11:12, 14 January 2008 (UTC)
- Notice that Runge's sphere has nothing to do with HSL or HSV. I'm also not really sure what the question is about, which is listed at wikiproject mathematics. I have university mathematical experience which extends significantly beyond the issues in question here, if that is of any use, and should be able to answer any specific mathematical questions SharkD has. --jacobolus (t) 12:18, 14 January 2008 (UTC)
- Runge's image shows a mapping of colors to a sphere based on their hue, saturation and lightness components. How does this not have anything to do with HSL? SharkD (talk) 20:26, 14 January 2008 (UTC)
- I agree that in the cartesian coordinate system, the hue and lightness parameters of the color at point (0,0,0) of a sphere is undefined. However, this is not the case in the spherical coordinate system. In this system, each coordinate has a unique color. The same is true for the cone and double cone; e.g., colors coalesce to a single point (or two points in the latter case), and at these points (white or black), the saturation parameter is undefined. Additionally, at any point along the central axis the hue parameter is undefined. The spherical, cylindrical and conical depictions are simply mappings of the HSL cube to the spherical, cylindrical, and conical (if such a thing exists), double-conical (ditto) coordinate systems. Any limitations in these particular depictions are the same as you find in any depiction of these coordinate systems. SharkD (talk) 20:33, 14 January 2008 (UTC)
- Can you make a sketch (pen and paper, or MS paint, or whatever, would be sufficient; doesn't have to be a masterpiece) of how you think this spherical organization of HSV is supposed to work? Because I don't have the foggiest idea what you're talking about in your description above. --jacobolus (t) 20:38, 14 January 2008 (UTC)
- I've provided three diagrams already, as well as a formula. Should this not suffice? SharkD (talk) 22:02, 14 January 2008 (UTC)
- I agree that your formulae and descriptions do make it clear; not sure why Jacobolus isn't getting it. But you haven't addressed the problem that several have pointed out: this embedding of HSL into a sphere does not preserve the different neutral colors as distinct points. Other embeddings could easily do so. Let me know if you'd like me to write you some equations. As to the Runge Farbenkugel, it's unclear what he took the parameters to be. HSL hadn't been invented, nor the RGB that it's defined in terms of; Runge's system is clearly based on RYB, but beyond that I don't know. Dicklyon (talk) 22:30, 14 January 2008 (UTC)
- I've already agreed with the fact that pure unsaturated values are not represented as distinct points. Here's a pretty good description of Runge's color sphere. Also, I find it kind of ridiculous to
sayimply that Alvy Ray Smith invented the notions of hue, saturation and lightness. SharkD (talk) 23:42, 14 January 2008 (UTC)
- I've already agreed with the fact that pure unsaturated values are not represented as distinct points. Here's a pretty good description of Runge's color sphere. Also, I find it kind of ridiculous to
- Alvy Ray Smith certainly did not invent the notion of hue. He did however first describe these HSL/HSV transformations of RGB, which is what is being discussed in this article. --jacobolus (t) 01:27, 15 January 2008 (UTC)
- Yeah, it's pretty silly to jump from the fact that he invented the HSL and HSV colorspaces as mappings of RGB to the strawman idea that he invented the notions of hue, saturation, and lightness. He didn't invent them, he adopted them, and made up the mappings that we call HSL and HSV. Dicklyon (talk) 04:14, 15 January 2008 (UTC)
- How is this a strawman idea? You questioned the validity of Runge's model based on HSL and RGB not having been invented yet. If HSL and HSV are just transformations of RGB, then what relevance do they have to other parameterizations of hue, saturation and lightness, such as Runge's model? If HSL isn't a parameterization of hue, saturation and lightness, then why is it being compared to other parameterizations of color, such as RGB and CMYK? SharkD (talk) 05:35, 16 January 2008 (UTC)
- “If HSL and HSV are just transformations of RGB, then what relevance do they have to other parameterizations of hue, saturation and lightness, such as Runge's model?” – they have none, except inasmuch as Alvy Ray Smith and his collaborators were inspired by other color models they had seen. HSL and HSV are just (modulo trivialities) 1:1 warpings of RGB into a shape intended to be more useful and intuitive for humans than a cube. They are nothing more, which is why I hesitate to call them “color spaces”, as the term is easy to misinterpret. --jacobolus (t) 10:44, 16 January 2008 (UTC)
- From the article I linked to: "Each colour placed on the surface of the sphere can move in five directions: towards the colours to the right or to the left; up towards white; down towards black; and inwards to the pass the grey of the centre and continue in the direction of its complementary colour." This description is accurate for both models. Other aspects are different, however. SharkD (talk) 04:02, 15 January 2008 (UTC)

- Sorry, I should have been clearer. It's not that I don't understand what your formulae say; it's that I don't think they are actually mapping HSL to a useful graphical description, and the mapping they do have doesn't match your diagram. Maybe a picture can help you understand what I mean. --jacobolus (t) 01:25, 15 January 2008 (UTC)
- Your math is wrong. SharkD (talk) 03:01, 15 January 2008 (UTC)
- Sorry, I should have been clearer. It's not that I don't understand what your formulae say; it's that I don't think they are actually mapping HSL to a useful graphical description, and the mapping they do have doesn't match your diagram. Maybe a picture can help you understand what I mean. --jacobolus (t) 01:25, 15 January 2008 (UTC)
- J, are you sure that's not an HSV sphere? In HSV with V at the latitude, all the bright saturated colors come together at the North pole. I figured that's why SharkD had only done HSL. It might be nice to have a mapping that would work for both. It ought to be dead simple to instead start with the assumption that neutral axis of the cylinder maps to the axis of the sphere, linearly or otherwise, and then map the rest sensibly; one easy way is to replace the z-dependent radius factor in the cone formula with a factor that makes the cross section circular instead of triangular; there are probably other good ways; still, you probably don't want to do this for HSV, just HSL.
- Ah, indeed. Blargh. Maybe I'll try to make a version properly showing HSL if I feel particularly ambitious. In any case, most of the problems with this direct spherical mapping apply to both equally, for instance having near-blacks sweep out an entire cone from the bottom of the sphere, collapsing all neutrals to a single point, and generally compressing unsaturated colors to a tiny fraction of the size they'd take in any perceptually-based representation. SharkD: how about this: You find a reliable source which uses such a spherical representation of HSL or HSV, and we'll mention it in the article. Otherwise, we'll take it out. --jacobolus (t) 04:26, 15 January 2008 (UTC)
- I concur. The first few HSL spheres I found here have L on the axis; I doubt that anyone has ever done otherwise. Dicklyon (talk) 04:50, 15 January 2008 (UTC)
- I created a diagram showing why mapping lightness to the vertical axis won't work. As you can see, the coordinates (0.9, 0.4), (0.8, 0.3) and (0.3, 0.2) don't exist in the diagram. If you move up a few units along the z-axis (lightness), the circles of radius (saturation) don't always intersect with
themthe lines. In order for the lines to always intesect the circles, they would have to be perpendicular to the tangent of the circles. If you look at the parametric equations for the cube, cylinder and cone you'll see that the z component is equal to a point along the z-axis. The z component of the parametric equation for the sphere is equal to the cosine of the angle phi. In order for lightness to be mapped to the z-axis in a sphere, the z component would need to equal a point along the z-axis, which would result in a cylinder. I think the mapping of lightness to the vertical axis in the articles is simply a mistake, and they meant to map it to the center. At least, they attempted to map HSL to a sphere. I believe this to be notable. SharkD (talk) 03:44, 16 January 2008 (UTC)
- I created a diagram showing why mapping lightness to the vertical axis won't work. As you can see, the coordinates (0.9, 0.4), (0.8, 0.3) and (0.3, 0.2) don't exist in the diagram. If you move up a few units along the z-axis (lightness), the circles of radius (saturation) don't always intersect with
- You could also argue that a cone doesn't work, for the same reason. But make it work; paraphrasing from your cone above:
- Here is the parametric formula for a cone modified into a sphere:
- Substituting H, S, and 2L–1 in for theta, r, and s results in a sphere, or radius 1.
- Try it? Dicklyon (talk) 05:34, 16 January 2008 (UTC)
- Oh, and use to make it a bi-cone. Dicklyon (talk) 05:38, 16 January 2008 (UTC)
- Since the top of the cylinder is all white, and the bottom is all black, shrinking these surfaces to the poles reduces those colors to single points. That's why the bi-cone is a natural form, and the sphere ain't so bad, too. Dicklyon (talk) 05:41, 16 January 2008 (UTC)
- Indeed, this is the sort of mapping I think most people who've ever tried to cram HSL into a sphere (or HSV into a hemisphere) have used. It's what I expected you meant, SharkD, before you specified otherwise (way up above in the discussion). I personally don't think it's particularly useful, as it isn't any closer to perceptually uniform or intuitive than the bi-cone version, and it adds some complexity to the arithmetic, so it is also less mathematically intuitive. But there certainly are sources which draw HSL in such an arrangement, such as the one Dicklyon linked to earlier. --jacobolus (t) 08:43, 16 January 2008 (UTC)
- Your parametric function doesn't work. In your equation, the "radial" arcs all intersect the point on the sphere where lightness is greatest. A sphere is all points equidistant from a point. This distance is called the radius. The articles all specify that saturation proceeds with the radius of the sphere. Therefore, your model is not the one given in the articles. Further, in the model I provided, lightness does map roughly to the z-axis. The angle phi is measured in angles around the center of the sphere, starting from one pole and ending at the other. These points can be measured roughly along the z-axis. The colors do not get darker again as you continue along the circle, because the angle phi stops at 180 degrees. SharkD (talk) 04:25, 17 January 2008 (UTC)
- I'm not sure what you mean by radial arcs, but saturation maps linearly from the center to the maximum radius of the constant-L disc, as in the cone; the solid is still a sphere, or maybe a "ball". Which ref says saturation maps radial in the sphere? I've looked and have not found anything so specific. Where the one says "moving from the center of the sphere outward", that needs to be interpreted in light of the statement that "near the center of the sphere colors are desaturated," where by center they obviously mean the central axis, since they already said "In the middle of sphere, dark colors are at the base (black), and light colors (white) are near the top, with a range of grays in between." My parameterization fits their description. The other ref says saturation increases from the "central core" outward; think of an apple core. Dicklyon (talk) 05:46, 17 January 2008 (UTC)
- I just created an image where I took the parametric version of the sphere and filled in the areas corresponding to non-vibrant colors, and it looks a lot more like an apple core. SharkD (talk) 01:46, 29 December 2008 (UTC)
- No, you could not argue that the cone doesn't work for the same reason. I've created a diagram showing why. As you can see, the lines of height always intersect the lines of radius. You guys are
reallyshowing a lack of understanding of mathematics. SharkD (talk) 01:26, 17 January 2008 (UTC)
- No, you could not argue that the cone doesn't work for the same reason. I've created a diagram showing why. As you can see, the lines of height always intersect the lines of radius. You guys are
- Sure, we know the cone works; my point was that for a cone or a sphere, or whatever, you can draw the picture that makes it work, and you can draw a picture that makes it not work. It's all about what parameterization you choose. Choose one that works, instead of a strawman that doesn't. Dicklyon (talk) 01:30, 17 January 2008 (UTC)
I've now removed the sphere image. As Dicklyon states most sphere reps have l running along the axis. Runge image predates the HSL colour-space and does not apply numeric quantities so that can not be used as a reference. A lack of WP:RS to colour system parametrised in this way means that the image classes as original research so should not be included. --Salix alba (talk) 10:23, 16 January 2008 (UTC)
- I think that if the sphere can be recreated with L on the axis, then it should be restored, as an illustration of the mappings that are referred to in the refs I noted above, even though those don't get into detail of exactly how they completed the parameterization. Dicklyon (talk) 16:21, 16 January 2008 (UTC)
- I think the lack of information would make this representation original research. SharkD (talk) 02:38, 17 January 2008 (UTC)
- Well, it's true that the proposed parameterization is not unique in its correspondence to the descriptions here and here, but it's harder to imagine or describe the alternatives. The mapping I described has L mapped linearly along the axis (the simplest interpretation of what they say), and L constant in planes orthogonal to the axis (like in the cone mapping), and circles of hue as they say, and saturation mapping linearly to radius within the planes of constant L, again pretty much as they state. I don't think I did anything originally in writing down the equations for this most-obvious interpretation of how to embed HSL or HSV into a sphere; the only plausible alternative is to warp the surfaces of constant L, but why would you want to? Dicklyon (talk) 03:41, 17 January 2008 (UTC)
- Well, regardless, the sources are ambiguous regarding how they map S to the sphere. Source #1 specifically says, "from the center of the sphere outward". Source #2 says, "from the center core outward". It's not clear what source #2 considers to be the "core" of the sphere, e.g. whether it is the common notion of the core of a spherical object, such as a planetary core or a solar core, or something else. I suggest these sources be removed from the article, as they do not support any statement made in the article.
- As for Runge's and Munsell's spheres, Runge's sphere is obviously not parameterizable (going from the diagram presented in the article). Munsell's sphere, on the other hand, does use the system you describe. SharkD (talk) 06:52, 18 February 2008 (UTC)
- Much later reply. I looked over the sources again, and I think it's pretty clear this time that they (except for Runge, whose model is broken, regardless) are referring to the model described in the article. I changed the text to better reflect this. SharkD (talk) 06:04, 29 June 2009 (UTC)
- Well, it's true that the proposed parameterization is not unique in its correspondence to the descriptions here and here, but it's harder to imagine or describe the alternatives. The mapping I described has L mapped linearly along the axis (the simplest interpretation of what they say), and L constant in planes orthogonal to the axis (like in the cone mapping), and circles of hue as they say, and saturation mapping linearly to radius within the planes of constant L, again pretty much as they state. I don't think I did anything originally in writing down the equations for this most-obvious interpretation of how to embed HSL or HSV into a sphere; the only plausible alternative is to warp the surfaces of constant L, but why would you want to? Dicklyon (talk) 03:41, 17 January 2008 (UTC)
Hole in the middle
You know, I just considered that adding a small gap in the middle would eliminate the issues raised with the first sphere model. SharkD (talk) 01:27, 29 December 2008 (UTC)
Merge HSL and HSB/HSV articles into one
- These two color spaces are both simple transformations of some RGB space (more like other ways of representing the same space, than spaces of their own). Unlike XYZ, CMYK, Munsell, or CIELAB, they are all based on the same device-dependent additive RGB color model.
- They have a similar intent (make relationship between RGB colors a bit more intuitive), and much of the information about the two is overlapping. That is, explaining both isn't much more complicated than explaining one of them.
- The spaces are commonly confused, and referred to by each-others abbreviations, and putting them on one page allows the explanation of which is which to be made explicit and clear, preferably with comparative diagrams (I'm willing to make such a diagram).
- If left separate, each needs a lengthy "comparison to the other" section. (Indeed, most of the HSL article already consists of comparison with HSV!)
- The comparison of each of these spaces to other common color models is essentially the same.
- There isn't all that much to say about the combination of the two articles. Merging the articles together, and filling in the coverage gaps, won't make for an inordinately long article.
- Both articles need cleanup, and in the merge I think overall quality would improve.
So in general, I think it makes sense to combine them (titled “HSL and HSV color spaces” or similar). Additionally, the information should be summarized and put in a section of RGB color model. --jacobolus (t) 10:35, 16 September 2007 (UTC)
- Is there really no one with an opinion about this? --jacobolus (t) 18:49, 4 October 2007 (UTC)
- I agree to a merge. Thanks for pushing on it. Dicklyon 20:39, 4 October 2007 (UTC)
- Well, if there are no objections soon, I'll hop to it. See the below section for my todo list for this article. --jacobolus (t) 21:44, 4 October 2007 (UTC)
- Once these are merged, what's the best title for the article? I'm thinking just "HSL and HSV" might be appropriate. --jacobolus (t) 10:00, 5 October 2007 (UTC)
Okay, so the articles have been nominally merged. I left out a couple bits of the HSV article that I don't think are ultimately needed, for instance the distracting animated images (there was agitation for their removal on the HSV talk page anyway), and the section about complements, which better fits under the "motivation" section in the new article. In the next few days we can move to the todo list from the section below. --jacobolus (t) 13:07, 5 October 2007 (UTC)
- I'm a bit late, I know. But, I think that merging the articles simply adds to the confusion. SharkD (talk) 20:02, 12 January 2008 (UTC)
- The real problem is that I never did my planned rewrite, or moved the article title to something like HSV and HSL. But even in its current state, this article is much less confusing than the pair which came before, in my opinion. --jacobolus (t) 20:05, 12 January 2008 (UTC)
- Well, the article should at least be renamed to reflect that it discusses both topics. Also, the article states that the two systems are related. They may be similar, but I'm not sure they're related, historically. SharkD (talk) 20:12, 12 January 2008 (UTC)
- They're related in that they were both proposed by the same author, in the same paper. Dicklyon sent me a copy of the paper, and it's now been 3 months that I've been sort of meaning to rewrite most of this article. But I've gotten busy with one thing after another, and a proper rewrite is going to take several hours. --jacobolus (t) 21:08, 12 January 2008 (UTC)
- That would be Alvy Ray Smith's "Color Gamut Transform Pairs," 1978. I can send a copy if anyone else wants to work on it. He proposes and constrast the HSV hexcone model and the HSL triangle model. I'd like to see better illustrations in terms of the actual 3D shapes of these spaces as defined, rather than warping them to cylinders or spheres. Dicklyon (talk) 23:19, 12 January 2008 (UTC)
rewritten intro, lowercase letters in formulae, todo for the next few days/weeks
I mostly rewrote the intro (and it's now in a form that should be easy to merge in HSV, which I'll try to do in the next few days, so raise any objections ASAP), to hopefully be a bit clearer and more accurate. I also lowercased the variable names in the formulae, which distinguishes coordinates from their corresponding axes, and looks cleaner, I altered some of the explanatory text between formulae, and I put the conversions under a single subheading. Still on the todo:
- Make some better images, that show the spaces as the cylinders they are defined as mathematically, and then show how those cylinders are deformed representations of cones or hexacones or spheres or whatever.
- Compare HSL/HSV to straight RGB, and better explain the motivation for expressing things by these color attributes instead of contributions of various primaries.
- Discuss the shortcomings of HSL/HSV, and compare to L*a*b* and Munsell systems, highlighting the trade-off of "fits in a nice box" and "easy to compute" and "based directly on RGB values from the screen" versus "perceptually-uniform". Explain that HSL/HSV co-opt the words "brightness", "lightness", and "value" (not to mention hue and saturation) to have different meanings than their usual technical definitions.
- Discuss the history of the use of HSL/HSV. I'm not too knowledgeable here so help would be appreciated.
- Prune out some of the cruft that's currently in the article
- Add some references—Help would also be appreciated with this one.
-jacobolus (t) 21:10, 4 October 2007 (UTC)
- The required cruft pruning has been magnified about 3× by the merger. :) --jacobolus (t) 13:08, 5 October 2007 (UTC)
- I found an interesting web site with some history of color models. The history of the Ostwald Colour System is here: http://www.coloracademy.co.uk/ColorAcademy%202006/subjects/ostwald/ostwald.htm#. Supposedly this was what the HLS model was based on (according to Alan Watt, 3D Computer Graphics, Second ed., 1993, Addison-Wesley Publishing Company, page 420), even though it is similar to HSV. History of the first 3D figures for the specification of color is here: http://www.coloracademy.co.uk/ColorAcademy%202006/classification/classification.htm, color terms like value and lightness and history related to color terms is here: http://www.coloracademy.co.uk/ColorAcademy%202006/subjects/parameters/parameters.htm, history of the Munsell color system is here: http://www.coloracademy.co.uk/ColorAcademy%202006/subjects/munsell/munsell.htm. These are all part of the web site of the "Color Academy" in the UK. They have other color system history and color science info as well. Their home page is: http://www.coloracademy.co.uk/ColorAcademy%202006/homepage/main.htm.Seaandsky 18:12, 20 October 2007 (UTC)
Examples of RGB and HSV or HSL images in the main article
In the sample images on the right side of the article -- the Lightness (and Value) image is shown in "redish" coloration. The three HSL components of the RGB image should be in gray level (monochrome images) since each pixel in these images has only a single value. For instance, according to the article, L =1/2(min+max). There are no 3 color components to show a given pixel in color.
BTW, PainShopPro separates color images into HSI (or RGB or CYMB) and these are displayed as monochrome.
Just a suggestion to reconsider the examples.
N. Gat 67.111.26.178 22:32, 10 October 2007 (UTC)
- I didn't make any of those channel separation examples, but the several people who did make them (a year ago) made HSV, HSL, Lab, CMYK, RGB, YCrCb, YUV, YDbDr, YIQ, and maybe a few more besides, all of which are colored similarly. --jacobolus (t) 01:36, 11 October 2007 (UTC)
- It's possible that the saturation, lightness, and value images are shown in red because in HSV and HLS, red corresponds to a hue of 0 (this was arbitrarily chosen for these systems, as far as I know). Thus, the hue image shows actual hues, and the other images show saturation, lightness, and value with a hue equal to 0. I don't know if that's what the creator(s) of those images had in mind, but it seems likely, especially if they were showing HLS and HSV in context with other color models, where a hue of 0 may be assigned to some other color. Of course, for the purposes of illustration, you might just as well choose to display gray images. It would just be a matter of preference or purpose. Seaandsky 15:54, 11 October 2007 (UTC)
- And actually, in this specific case, I'd personally prefer to have hue and saturation shown with colors, and value/lightness/brightness/whatever shown in gray. But the current ones are fine enough that I'm not going to bother changing it myself. :) --jacobolus (t) 16:22, 11 October 2007 (UTC)
- I had never really looked at those before, but now I think I see their point. The H is shown as an image of variable hue with a chose (max) saturation and value. The S is shown as a image of variable saturation, for some chose hue and value. And the value is shown as variable value with fixed hue and saturation. The latter could choose saturation 0 and make it gray. But the S image can't be shown without a color, and picked hue 0 for that. Confusing, but with a certain logic. Dicklyon 23:51, 11 October 2007 (UTC)
- I think they should be in grayscale, as well. All image creation software does so in this way, as far as I know. SharkD (talk) 20:04, 12 January 2008 (UTC)
The inconsistency of these images bothered me too. That's why I made ones of my own. see my gallery. I'm not confident enough to put them into this article. Maybe one of you knows their way around a page edit :P --Crackwitz (talk) 01:48, 20 August 2009 (UTC)
Rename
I think the article should be renamed to HSL and HSV color spaces to avoid confusion. SharkD (talk) 21:01, 13 January 2008 (UTC)
- What confusion? I'm a bit leery of explicitly calling them “color spaces” (a term for which I have never seen a particularly precise definition) because they are properly simple coordinate transformations of RGB, with each RGB color space having its own unique corresponding HSL and HSV representations. --jacobolus (t) 04:27, 14 January 2008 (UTC)
- The confusion resulting from readers not being informed that HSL and HSV don't refer to Hawaii State Library and Holden Special Vehicles. SharkD (talk) 06:00, 14 January 2008 (UTC)
- Erm, why in the world would there be a single article about the two of those? And who would have any doubts about it after the first sentence? It's not like either HSL or HSV redirects here. --jacobolus (t) 12:17, 14 January 2008 (UTC)
Italicized HSV, etc.
Hi Dicklyon,
I had previously consistently labeled the components/axes of the space as H, S, V, L, etc. while consistently naming particular values (i.e. vector components) as h, s, v, l (and using italicized HSL, HSV, RGB, L*a*b*, etc. for those names). I think such naming is the best way to keep such distinctions clear. I noticed you changed upper-cased H, etc. for lower-cased h, etc. in a few cases, and otherwise removed a large number of my italics. I believe this to be a regression in article quality, though my naming convention is obviously less useful/clear than it would be had I completely rewritten the rest of the article, rather than just the introduction and formulae sections. --jacobolus (t) 12:36, 14 January 2008 (UTC)
Similarly, given that min and max are variable names, setting them in roman is misleading. I suppose greek letters or something could be used instead of min and max. I think though that the named variables make the formulae clearest. --jacobolus (t) 13:25, 14 January 2008 (UTC)
- I think the H vs. h distinction might have something to it, but I see no precedent for italicizing the acronyms. As to the min and max, that was someone else's change, but I like it better than what we had before, where min appeared to represent m*i*n. There's no great way to mix computer-style naming with math-style. Dicklyon (talk) 16:04, 14 January 2008 (UTC)
I see RGB every where…
"These two color spaces are both simple transformations of some RGB space" I not agree with that. It seems to be a common idea and it's false. Models are independant at a first time. RGB space got only one white and one black, that why the double cone representation is well known. A true HSL space permit things that a RGB one doesn't. Decrease then increase light: in HSL a black can come from a red and return to this red; in RGB a black coming from red return to gray. HSL have choose a natural color space that can be fully converted to a RGB space but with data lost. HSL->RGB is non-injective and surjective. If it was a transformation of RGB, it would have been injective. (Or in another words, RGB->HSL would have been surjective.) As a digital painter, I'd like to have a software supporting a real HSL color space. RGB is a display color space. HSL could be a great creation color space. Lacrymocéphale
- You are correct that it is not strictly a bijection, in that, in HSL, all points such that l = 0, and in HSV, all points such that v = 1, or v = 0, map to single points in the corresponding RGB space. However, given that all such points also represent a single color—and all other points, those which represent different colors, do map bijectively onto the corresponding RGB space—this is more a design flaw (i.e. they were designed for computational convenience, not theoretical elegance) with HSL/HSV, than it is an obstacle to thinking of them as a simple transformation of RGB. The rest of your statement is misinformed and garbled: black does not “come from” red, and HSL would not be no different for “creation” than RGB, because they are representations of the same model, transformed in a very rough way, and have little to do with human visual-perception: use something like L*a*b* instead, if you are looking for an intuitive color space. --jacobolus (t) 19:06, 14 January 2008 (UTC)
- I think that Lacrymocéphale is clearly not a native English speaker. What he means is that, in HSL, colors can easily transition ("go to", "come from") between black and red. In other langauges, this is the proper usage. Also, I think the two of you have different definitions of "intuitive". From the end-user (e.g., artist's) standpoint, L*a*b* is the very definition of unintuitive. SharkD (talk) 03:33, 15 January 2008 (UTC)
- No, from an human visual perception perspective L*a*b* is much more intuitive, at least in L*Ca*b*ha*b* form (which basically has lightness, hue, colorfulness dimensions, but unlike in HSL/HSV they are actually consistent and meaningful). RGB has very little to do with human perception of colors. It's just that people have been taught models like RGB. This makes them learned, not intuitive. But quick, tell me what you get if you combine 30% R, 25% G, 80% B, and what's the relationship of that mixture to the same, but with 70% R instead. If you have to plug those into a computer or think hard about it to answer, that means the model isn't intuitive! If you tell me the number of a color in L*Ch or Munsell, I can picture that color in my head instantly. --jacobolus (t) 00:03, 18 February 2008 (UTC)
- If L*Ch is simply a transformation of L*a*b* so that the input values correspond to Lightness, Chroma (Saturation) and Hue, then there is zero difference in intuitiveness. As for HSL and HSV not having meaningful values, they are in practice a transformation of sRGB space and are therefore no more or less device-independant than L*a*b*. SharkD (talk) 05:24, 18 February 2008 (UTC)
- Duh … L*Ch isn't even really a transformation of L*a*b*, but just the same thing expressed in polar coordinates, an expression which is easier to visualize and grapple with; my claim is that L*a*b* is more intuitive than RGB. HSL/HSV lack meaning w.r.t. human vision because of their origin in RGB (whether sRGB or another space) and device-dependence or -independence has little to do with it. --jacobolus (t) 08:48, 18 February 2008 (UTC)
Open interval
The function for converting RGB to HSL could be rewritten in such a way such that the interval for Hue is closed. I don't know where you got your function from. But, all the ones I've found on the Net only are closed. SharkD (talk) 18:16, 17 February 2008 (UTC)
- I thought they all defined the hue of red as 0, not 360, meaning it's semi-open. Which ones allow for red to be 360? Dicklyon (talk) 23:19, 17 February 2008 (UTC)
- Alvy Ray Smith's paper defining it has a half-open interval
- Ah, I thought an open interval meant that the function allowed values beyond 360, such as 720 or 1080. My mistake. SharkD (talk) 03:27, 18 February 2008 (UTC)
HSL definition
The text says that "Both models were first formally described in 1978 by Alvy Ray Smith". Unfortunately, reading through the article, it is clear that the HSL model the author is talking about is definitely not the HSL we are referring to in this page. Does anyone know any other source? --Prydeson (talk) 16:53, 21 March 2008 (UTC)
- Actually as described in the paper, it's a generalization (allowing various other specific interpretations) of the model described in this article. I've been meaning for months to rewrite this to better explain that, but I'm not doing a very good job getting around to it, and am extremely busy for the next few weeks; grr.. --jacobolus (t) 20:30, 21 March 2008 (UTC)
"Intuitive" HSV/HSL to RGB
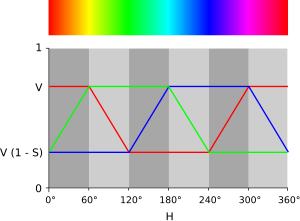
I find the HSL/HSV to RGB conversions horribly unintuitive, mostly because the case distinction over H is kept until the end. I would find it more comfortable to have a fully saturated color, then "apply" SV and SL to it, respectively. Both the SV and SL "transformations" do not depend on the hue and are equal for all three RGB channels (I will just use C as placeholder below).
for HSV, that would be:
- Compute the fully saturated color according to the image on the right.
- Apply saturation: We basically scale the RGB values toward 1 (white), i.e. the difference to 1 is scaled down, 1 is a fixed point:
- Apply value: We simply scale the RGB values toward 0:
and for HSL:
- Compute the fully saturated color according to the image on the right.
- Apply saturation: We basically scale the RGB values toward 0.5 (gray), i.e. 0.5 is a fixed point:
- Apply lightness. This is the nasty part:
- for : The color gets darker, black for and unchanged for . This means scaling toward 0.
- for : The color gets lighter, white for and unchanged for . This means scaling toward 1. Because we want to yield (i.e. scale 0), the scaling factor is (and not ).
- note that for , both cases do nothing.
- for : The color gets darker, black for and unchanged for . This means scaling toward 0.
Would be cool if somebody could verify these algorithms and eventually include them in the article. Thanks! MoA)gnome (talk) 20:25, 25 July 2008 (UTC)
- I'm not sure I understand the chart at right. Why don't the saturation values go from 0 to 1? They seem to instead go from 1/4 to 3/4, if I read the y-axis correctly. SharkD (talk) 02:54, 8 September 2008 (UTC)
- The caption appears to be misleading. The range of values has been adjusted based on S and V values less than 1. The illustration is for about V=0.75 and S = 0.7, looks like. Dicklyon (talk) 04:26, 8 September 2008 (UTC)

- Yeah, sorry, I took the image from the article without paying attention to the fact that the values are in a smaller interval. What I mean by "fully saturated" would be the curves stretched vertically so they reach from 0 to 1; i.e. the possible "initialization" colors are the ones in the color band above the curves. —MoA)gnome (talk) 22:31, 11 September 2008 (UTC)
- On a side note, what I described exactly corresponds to moving through the according color "cylinder" (image also taken from the article). HSV (right) starts at the upper edge, HSL on the outside at half the height. Applying S means moving toward the center, applying V/L, respectively, means moving down or up (there's no moving up for HSV, of course). —MoA)gnome (talk) 22:51, 11 September 2008 (UTC)
- If the image accurately reflects what you describe, then what you describe is already covered by the article. SharkD (talk) 23:32, 11 September 2008 (UTC)
- I am not saying that this is anything new. My point is just that the HSL/HSV to RGB conversions are quite obscure IMHO; it is hard to tell what saturation and lightness/value do to the quasi "initial color" that I called "fully saturated". The cylinder image does reflect it, though. —MoA)gnome (talk) 21:06, 13 September 2008 (UTC)
- If the image accurately reflects what you describe, then what you describe is already covered by the article. SharkD (talk) 23:32, 11 September 2008 (UTC)
- Ah, I see. I automatically assumed that the hue gradient at the top of the image was fully saturated/valued. I expect that other readers might also become confused by this. SharkD (talk) 01:23, 29 December 2008 (UTC)
- OK, I lied. I still don't get it. SharkD Talk 04:26, 2 February 2010 (UTC)
I’ve tried to put in more intuitive conversions. What do you think? –jacobolus (t) 22:12, 5 February 2010 (UTC)
HSL to RGB Color Conversion
The article currently sates that for RGB to HSL conversion L=(min+max)/2... Shouldn't this be L=(R+G+B)/3? As it now sits, the RGB components (0,0,254) and (0,254,254) would both produce a luma value of 127. I do not believe this is correct... --Electrostatic1 (talk) 02:28, 8 September 2008 (UTC)
- NM, I get it now... 0,0,255 would be fully bright and saturated blue, 0,255,255 would be fully bright and saturated cyan... —Preceding unsigned comment added by Electrostatic1 (talk • contribs) 02:38, 8 September 2008 (UTC)
- You are right that (0,0,255) and (255, 255, 0) have significantly different luminance, lightness, etc. Realize that the L of HSL has only vague resemblance to physical or perceptual qualities. The HSL/HSV described in this article are historical artifacts from the 1970s whose usefulness has passed, but are still used because software devolopers are ignorant or lazy (mostly ignorant). —jacobolus (t) 06:18, 8 September 2008 (UTC)
- I don't know... the L in such models as Lab or the Munsell system seem "fraudulent" somehow; kinda like someone else is deciding for you what the best values for lightness are instead of letting you decide for yourself. SharkD (talk) 15:57, 28 December 2008 (UTC)
- Isn't that what a standard color space is supposed to do? Have someone else decide the coordinates for you, instead of a bunch of people making incompatible decisions for themselves? Dicklyon (talk) 18:06, 28 December 2008 (UTC)
- Well, for the typical form of HSL the discrete steps for L are mapped more or less linearly to particular emissions of the phosphor diodes on a computer monitor (assuming all monitors share the same gamut). Since models like Lab are based on human perception, it's a lot harder to turn around and derive the original wavelengths of the source emissions based on a given tuple of coordinates. For example, let's say that a hypothetical color space interpolated across a range of wavelengths at intervals of 50nm. The calculations are a lot easier than if the color space instead interpolated at shorter intervals where human sensitivity is greater and longer intervals where it is less sensitive. I just personally feel that doing things like finding complementary colors and performing other color matching is a lot harder when the numbers themselves have been adjusted in some way. It's kind of like psychoacoustically-compressed audio: they offer better data compression for a given perceived quality of sound, but they don't affect how we perceive sound or how we manipulate the source frequencies. I can definitely see the advantages of Lab: it's inefficient to calculate or store colors that you can't see anyway, and it's better to offer higher fidelity where humans can see in greater detail. But this added difficulty is probably why Lab isn't in wider use. SharkD (talk) 22:17, 28 December 2008 (UTC)
- “complementary colors” is not a particularly meaningful concept except w/r/t human perception, so using a non-perceptual space to compute them guarantees poor results. It’s physically impossible to derive the source emissions based on any finite tuple of coordinates. In typical HSL, the mapping is actually a gamma curve along each R, G, B coordinate, and this causes big problems in interpolation, etc. “Assuming all monitors share the same gamut” is an absurd assumption that will never be even close to true, even among displays of the same model number. And CIELAB’s advantage over RGB isn’t really about efficiency of calculation or storage (indeed, it’s less efficient for both). Finally, I don’t think this has anything to do with why perceptual spaces aren’t in wider use: that is much more an education problem than anything else. In 2009, the hardware limitations of the 1970s no longer apply. —jacobolus (t) 05:37, 1 July 2009 (UTC)
- Well, for the typical form of HSL the discrete steps for L are mapped more or less linearly to particular emissions of the phosphor diodes on a computer monitor (assuming all monitors share the same gamut). Since models like Lab are based on human perception, it's a lot harder to turn around and derive the original wavelengths of the source emissions based on a given tuple of coordinates. For example, let's say that a hypothetical color space interpolated across a range of wavelengths at intervals of 50nm. The calculations are a lot easier than if the color space instead interpolated at shorter intervals where human sensitivity is greater and longer intervals where it is less sensitive. I just personally feel that doing things like finding complementary colors and performing other color matching is a lot harder when the numbers themselves have been adjusted in some way. It's kind of like psychoacoustically-compressed audio: they offer better data compression for a given perceived quality of sound, but they don't affect how we perceive sound or how we manipulate the source frequencies. I can definitely see the advantages of Lab: it's inefficient to calculate or store colors that you can't see anyway, and it's better to offer higher fidelity where humans can see in greater detail. But this added difficulty is probably why Lab isn't in wider use. SharkD (talk) 22:17, 28 December 2008 (UTC)
- Isn't that what a standard color space is supposed to do? Have someone else decide the coordinates for you, instead of a bunch of people making incompatible decisions for themselves? Dicklyon (talk) 18:06, 28 December 2008 (UTC)
- I don't know... the L in such models as Lab or the Munsell system seem "fraudulent" somehow; kinda like someone else is deciding for you what the best values for lightness are instead of letting you decide for yourself. SharkD (talk) 15:57, 28 December 2008 (UTC)
- You are right that (0,0,255) and (255, 255, 0) have significantly different luminance, lightness, etc. Realize that the L of HSL has only vague resemblance to physical or perceptual qualities. The HSL/HSV described in this article are historical artifacts from the 1970s whose usefulness has passed, but are still used because software devolopers are ignorant or lazy (mostly ignorant). —jacobolus (t) 06:18, 8 September 2008 (UTC)
There is another problem in this section. We are given h, in . One of these statements is a lie: either h was in , hk is in
- Actually, it's not that much of a problem; if h is in . Fix the interval to be semi-open if it bothers you. Dicklyon (talk) 18:48, 7 November 2009 (UTC)
"such change of meaning should be accompanied by a source" (diff)
The original article text is unsourced and easily contradicted by reading the rest of the article. SharkD (talk) 03:24, 29 June 2009 (UTC)
- I'll add some sources. SharkD (talk) 03:38, 29 June 2009 (UTC)
- Thanks; correcting unsourced stuff with unsourced stuff is not generally a win. Dicklyon (talk) 03:42, 29 June 2009 (UTC)
"patch what's said about the RGB primaries back to what was intended" (diff) (newer diff)
"Values" would be a better word to use, since by themselves the R, G, and B primaries don't have a "color". I.e., colors need all three components; by themselves they have no meaning. SharkD (talk) 03:29, 29 June 2009 (UTC)
- I'm not sure what "values" refer to there, but each primary color certainly does have a color. Dicklyon (talk) 03:41, 29 June 2009 (UTC)
- I mean "value" in the same sense as "numerical value" or "value of the integer" (actually a float in this case). A color in the RGB model can't have just a R, G, or B value; it must have both of the other two values as well—even if they are set to zero. Also, using the word "color" makes it sound like the primaries could be something other than red, green or blue (which they of course can't). It's just a matter of choosing the right words for clarity. "Strength" might also be a good choice. I prefer "value" because it is used more often in mathematics and programming. SharkD (talk) 03:51, 29 June 2009 (UTC)
- Those values have nothing to do with the intended meaning; the intended meaning is about what the three primary colors are; the R primary has a color (a red), the G primary has a color (a green), and the B primary has a color (a blue); exactly what colors the primaries are will affect what color is represented by and RGB triple and hence an HSV triple. Dicklyon (talk) 04:53, 29 June 2009 (UTC)
- ..."exactly what colors the primaries are will..." The primaries can only be *one* color. The phosphors or LEDs don't change color; they only get brighter or dimmer. I.e. they vary in intensity or strength, not in color. I don't disagree with the meaning; I disagree with the wording. SharkD (talk) 05:03, 29 June 2009 (UTC)
- Sounds like you haven't understood the meaning yet. The "values" don't change the colors of the primaries; those are fixed, as you note. But fixed to what colors? Those are the primary colors being referred to here. Did you check the linked article on additive primaries at least? Dicklyon (talk) 05:12, 29 June 2009 (UTC)
- Sigh... I was hoping to avoid getting into an English/grammar debate. I'll request an RfC. SharkD (talk) 05:19, 29 June 2009 (UTC)
- I don't think it has to do with any language subtleties; just read what it says; it's very different from the concept you changed it to, which doesn't make a lot of sense, since the values of R, G, and B are completely determined by the values of H, S, and L. This is no ambiguity in the values, just in the colors that those values represent. Dicklyon (talk) 05:24, 29 June 2009 (UTC)
- Sorry!!! I see the problem now. I completely glossed over the first sentence in the paragraph and neglected the fact that the paragraph was dealing with the device-dependent nature of color models with respect to color spaces. My mistake! SharkD (talk) 05:44, 29 June 2009 (UTC)
L*Ca*b*ha*b*
Maybe L*Ca*b*ha*b* should be mentioned in the "Comparison with other color models" section? It's fairly similar. I can't find any references to it using Google, though. SharkD (talk) 05:56, 29 June 2009 (UTC)
- L*C*abh*ab and L*C*uvh*uv are just alternate (cylindrical rather than rectangular) representations of CIELAB and CIELUV. They could certainly be discussed, if you like. There are all kinds of references: search for "CIELAB LCh". —jacobolus (t) 05:18, 1 July 2009 (UTC)
Device independent image formats
Just a quick question: are there any web-safe device-independent image formats, or is that still several years down the road? SharkD (talk) 16:12, 30 June 2009 (UTC)
- I don’t understand the question. What is “web safe”? —jacobolus (t) 05:19, 1 July 2009 (UTC)
- Mainly I mean whether or not they are supported by browsers. SharkD (talk) 20:56, 1 July 2009 (UTC)
- Why would you think it might be "down the road"? Is there evidence that there's some interest in combining the "web safe" concept with the "device independent" concept? Dicklyon (talk) 00:16, 2 July 2009 (UTC)
Barn Image is Confusing
The barn image is confusing. What does it mean it has its RGB or HSL values displayed? More explanation about what is going on in each image would be really helpful. The one on the left is supposed to be R, G, and B, right? Why does one of them have yellow and blue in it? Shouldn't each one only have one color? Maybe break down each image with captions for each one explaining what's going on and what that means. Thanks! Saffolicious (talk) 05:44, 2 January 2010 (UTC)
- It has also been suggested that the images be presented in grayscale, as they are in most image editing programs. SharkD Talk 04:12, 4 January 2010 (UTC)
working on a nearly complete re-write
Hi everyone. At long last I've gotten sick enough of the state of this page that I'm working on a near complete rewrite. While I write it, I have it at Talk:HSL and HSV/replacement in progress, and I'll move it to HSL and HSV when it's ready to go. Feedback about my current outline or already written prose is welcome, but for now, don’t edit that page directly, until I’ve had a chance to write the complete article. I still need to make several more diagrams, among other things. –jacobolus (t) 04:16, 26 January 2010 (UTC)
- Firstly, the article probably should have been created in User space. But it's not a big deal.
- "Both of these representations are in very wide use in computer graphics, and one or the other of them is often more convenient than RGB, but both are also commonly criticized for not actually separating color-making attributes, and for their lack of perceptual uniformity." I understand the perceptual uniformity bit, but not the bolded part. Do you mean the photometric color-making attributes? If so, then you should say so. What do you mean when you say "separating"?
- It should be pointed out that the problems with regard to lack of perceptual uniformity in each of the models is inherited from RGB. I.e. HSL and HSV are perceptually inaccurate because RGB is.
- I like how you created File:Tint-tone-shade.svg. Some analog depictions of some of the other painters' terminology (chromaticity, nuance, etc.) would be nice to have as well.
- The section on "geometric derivation" is a bit convoluted. It needs copy-editing, and needs to be more concise.
- The article looks a bit like it's suffering from image soup. Putting some effort into arranging and aligning the images would help make the article appear a bit more organized.
- Lastly, I think the existing article is better suited for readers with less understanding (i.e. beginners). For instance, readers might want to go directly to the meat of the matter; what the model looks like, how it is used in the professional world, and the conversion formulas. Jumping directly into the derivation material is a bit like telling the recipe for Chicken Kiev before saying what it actually is. SharkD Talk 00:49, 31 January 2010 (UTC)
- Yes, it definitely needs a copyedit. The problems w/r/t perceptual uniformity, etc. still need to be described in detail, in the section "disadvantages". I don't know whether the geometrical derivation section can be made *too* much more concise and still explain how these things work. Great effort *has* been put into arranging the images, so that they flow properly; there might be some way of improving it a bit though. I think that the existing article is terrible for beginners, who are likely to be misled and left confused, since it is vague and imprecise, and does not extremely clearly state the problems with HSL/HSV. You might be right though that a section at the top with the “basic idea” might be helpful. I still have a way to go, in particular with adding images showing various cross-sections and 3-d renders of these models. I don't think the ones in the current article (e.g. near the top) do a good enough job. –jacobolus (t) 01:54, 1 February 2010 (UTC)
- I meant the images in the derivation section, sorry. The rest of the article is fine. I think changing the width of the second image to match the first and third would suffice. Also, you might want to temporarily lower your graphics card resolution. I browse at 1024x768 and things are cramped. SharkD Talk 04:12, 2 February 2010 (UTC)
- Yes, it definitely needs a copyedit. The problems w/r/t perceptual uniformity, etc. still need to be described in detail, in the section "disadvantages". I don't know whether the geometrical derivation section can be made *too* much more concise and still explain how these things work. Great effort *has* been put into arranging the images, so that they flow properly; there might be some way of improving it a bit though. I think that the existing article is terrible for beginners, who are likely to be misled and left confused, since it is vague and imprecise, and does not extremely clearly state the problems with HSL/HSV. You might be right though that a section at the top with the “basic idea” might be helpful. I still have a way to go, in particular with adding images showing various cross-sections and 3-d renders of these models. I don't think the ones in the current article (e.g. near the top) do a good enough job. –jacobolus (t) 01:54, 1 February 2010 (UTC)
- Yeah, it's a bit of a tricky trade-off. It currently looks best for browser windows of between 900-950 pixels wide. People using 800x600 resolution are definitely going to suffer a bit from the layout, as are people who size their browser windows to wider than about 1100 pixels (their wikipedia experience is just going to suck generally though, because every line of text will be way too wide). –jacobolus (t) 03:52, 3 February 2010 (UTC)
Okay, this is getting more complete. Continuing feedback is welcome (again, the page). –jacobolus (t) 00:27, 5 February 2010 (UTC)
- Does anyone have a good idea how I can make this section flow with the images it has, at all monitor widths? This is the best I could come up with, which works for widths 900-1050 pixels, but then leaves a bigger gap the wider the window gets after that. Maybe it's no big deal – people with wider browser windows are going to get a somewhat unpleasant Misplaced Pages experience regardless. I wonder if anyone knows, e.g., whether I can make images inline elements w/ wiki markup, so that as many will try to fit in each row as possible, flowing around the image above to the right. –jacobolus (t) 16:16, 5 February 2010 (UTC)
- As for the images spreading into neighboring sections, I would suggest combining the first two images in the 'Hue and chroma' sections into a single image, like this. Or, split them into three images and use the multiple image template. SharkD Talk 03:35, 6 February 2010 (UTC)
- The images in the 'Motivation' section could be combined into a single group like this. SharkD Talk 03:53, 6 February 2010 (UTC)
 Painters long mixed colors by combining relatively bright pigments with
black and white. Mixtures with white are called tints, mixtures with black are called shades, and mixtures with both are called tones. See Tints and shades.
Painters long mixed colors by combining relatively bright pigments with
black and white. Mixtures with white are called tints, mixtures with black are called shades, and mixtures with both are called tones. See Tints and shades. This 1916 color model by German chemist Wilhelm Ostwald exemplifies
the “mixtures with white and black” approach, organizing 24 “pure” colors into a hue circle, and colors of each hue into a triangle with corners of the “pure” color, white, and black. The model thus takes the shape of a bicone.
This 1916 color model by German chemist Wilhelm Ostwald exemplifies
the “mixtures with white and black” approach, organizing 24 “pure” colors into a hue circle, and colors of each hue into a triangle with corners of the “pure” color, white, and black. The model thus takes the shape of a bicone. This diagram, from a Tektronix patent filed in 1983, shows the bicone geometry underlying the HSL model.
This diagram, from a Tektronix patent filed in 1983, shows the bicone geometry underlying the HSL model.
 Colors are combined by adding values. (Should ideally use the same color as in the bottom image.)
Colors are combined by adding values. (Should ideally use the same color as in the bottom image.) The RGB gamut can be arranged in a cube.
The RGB gamut can be arranged in a cube.
- But one of the images is intended to flow with the text, while the others are supplementary/incidental. I don't like stacking them the way you have here: it seems extremely forced, and makes things harder to see. There's no reason to not just let images be big enough to read/etc. –jacobolus (t) 07:16, 6 February 2010 (UTC)
- A few more points: If you think it’s currently cramped for narrow browser windows, making a 460ish-pixel-wide and hundreds-of-pixels-tall block of images would be much worse. Especially since, in the narrow column next to them, not much text would fit, and so big blocks of text below would necessarily be full-width (and therefore less readable; we end up with the worst of both worlds, with a super narrow column for one part and a super wide one for another). The tint/tone/shade image is as small as it can reasonably be and still be readable, and if it's unreadable it's essentially useless and might as well be removed. I don't really care too much for the RGB cube image. I just put it in because I think we need some decent illustration of a cube, and this one was handy, already in (I think the German?) wikipedia; we could certainly make a different one. The tektronix patent image belongs as near as possible to the text about tektronix; it's a logically separate part of the text from the ostwald/tint-tone images, and sticking them together would be confusing. –jacobolus (t) 07:44, 6 February 2010 (UTC)
Break
This template must be substituted. Okay, I've started transferring things. –jacobolus (t) 17:21, 5 February 2010 (UTC)
- A couple of remarks
- I think the term "color model" should be used instead of "color space" except where specifically required. For instance, in the top image.
- I think that the 2D images of the cylindrical cross-sections (File:Hsl-hsv chroma-lightness slices.svg and File:Hsl-hsv saturation-lightness slices.svg) should be accompanied by 3D images of the actual solids. Not sure how you would create these in SVG. I don't personally own software tools that can do this. There's currently only one image in the article actully showing a 3D representation of the cylinders.
- Please use the same color in all the charts. For instance, in the first set, the color has a hue value of 200°; in the second set the color has a hue value of 230° (and its complement has a value of 50°).
- SharkD Talk 23:32, 5 February 2010 (UTC)
- What charts are we talking about? The hue/chroma and saturation sections use the same colors. As far as I know nowhere is a 200° hue used. I don’t think that the “cones” are actually useful to show at all, but I have a friend who is going to render 3d views of both HSL and HSV cylinders. –jacobolus (t) 00:19, 6 February 2010 (UTC)
- Oh, now I see what you’re saying. No, the difference is motivated by which best show off the effects we want to show: We pick a point 1/3 the way along an edge so that it’ll show a reasonable difference between H and H2, C and C2, for the "stick drawings", and the particular one chosen was in a convenient place for the 3d drawing showing the projection. By contrast, we pick slices that are quite close to blue/yellow for the lightness/chroma/saturation slice graphics because they best distinguish between different lightness definitions. –jacobolus (t) 00:39, 6 February 2010 (UTC)
- I think switching the colors (the input parameters) makes things harder to discern what is happening in the charts (the formulas). You want to keep the number of variables to a minimum when explaining something complex. In fact, I think it would be a good idea to plot the actual colors from the stick drawings in the lightness/chroma charts. SharkD Talk 00:53, 6 February 2010 (UTC)
- Try graphing them: the relationship is much less clear. –jacobolus (t) 01:00, 6 February 2010 (UTC)
- I mean something like this (except using the blue and corresponding yellow from the stick drawings). I think the blue and yellow from the stick drawing is sufficiently "close to blue/yellow" to highlight the differences in lighteness. SharkD Talk 01:47, 6 February 2010 (UTC)
- I think that just adds clutter, and doesn’t really help explain anything. I dunno.... maybe it’d be helpful for someone. –jacobolus (t) 02:14, 6 February 2010 (UTC)
- Also, no, it wouldn't help for the lightness drawings, because we want to have luma, component average, and HSL lightness be far apart and easily distinguishable. –jacobolus (t) 02:17, 6 February 2010 (UTC)
- I think that making the article easier to understand/more cohesive by tying the sections/images together would be better here than slight tweaks to elucidate one particular small piece of minutiae, especially when the changes are marginal. SharkD Talk 03:19, 6 February 2010 (UTC)
- Which “particular small piece of minutiae ” are you talking about? –jacobolus (t) 07:16, 6 February 2010 (UTC)
- I think that making the article easier to understand/more cohesive by tying the sections/images together would be better here than slight tweaks to elucidate one particular small piece of minutiae, especially when the changes are marginal. SharkD Talk 03:19, 6 February 2010 (UTC)
- I mean something like this (except using the blue and corresponding yellow from the stick drawings). I think the blue and yellow from the stick drawing is sufficiently "close to blue/yellow" to highlight the differences in lighteness. SharkD Talk 01:47, 6 February 2010 (UTC)
- Try graphing them: the relationship is much less clear. –jacobolus (t) 01:00, 6 February 2010 (UTC)
- I think switching the colors (the input parameters) makes things harder to discern what is happening in the charts (the formulas). You want to keep the number of variables to a minimum when explaining something complex. In fact, I think it would be a good idea to plot the actual colors from the stick drawings in the lightness/chroma charts. SharkD Talk 00:53, 6 February 2010 (UTC)
- Oh, now I see what you’re saying. No, the difference is motivated by which best show off the effects we want to show: We pick a point 1/3 the way along an edge so that it’ll show a reasonable difference between H and H2, C and C2, for the "stick drawings", and the particular one chosen was in a convenient place for the 3d drawing showing the projection. By contrast, we pick slices that are quite close to blue/yellow for the lightness/chroma/saturation slice graphics because they best distinguish between different lightness definitions. –jacobolus (t) 00:39, 6 February 2010 (UTC)
- Also, I think “color space” is more appropriate, as this depends completely on the particular RGB space in use: each RGB color space implies a different HSL/HSV representation. Whereas “RGB color model” to me indicates the overall idea of RGB. –jacobolus (t) 00:21, 6 February 2010 (UTC)
- Yes, that's exactly why I think "color model" should be used. HSL and HSV are transformations of the "overall" RGB model. If mapped to a particular color space, their shapes would look different based on the particular gamut used (such as in the sRGB and Adobe RGB images in the 'Disadvantages' section). Whereas a plot of the models' shapes would always remain the same. SharkD Talk 00:48, 6 February 2010 (UTC)
- Huh? I don’t know what “If mapped to a particular color space” means, in this context. If you plotted their colors in, e.g., CIELAB, you’d end up with the same gamut as the plots shown... because it’s the same colors either way, RGB or HSV. –jacobolus (t) 01:02, 6 February 2010 (UTC)
- As in, mapping the HSL and HSV color models to a particular color space. If you were to place the coordinates with respect to differences in gamut, then the resulting cylinder would be distorted in much the same way as the RGB cube is in the CIELAB images. SharkD Talk 01:55, 6 February 2010 (UTC)
- That doesn’t make any sense. You’d never try to compare gamuts of two RGB color spaces with respect to the HSV representation of one of them. It would just be a very complicated and arbitrary shape... and either way it has nothing to do with any distinction between “color model” and “color space”. –jacobolus (t) 02:14, 6 February 2010 (UTC)
- That's exactly what Munsell talks about in his books: a representation of gamut in a cylindrical (or sometimes spherical) space. And whereas generally labeling things as color spaces would be appropriate in an article about the Munsell system, it would not be here, except in sections specifically discussing their application to color spaces. SharkD Talk 02:40, 6 February 2010 (UTC)
- What? This all has nothing to do with Munsell; he predates the term “color space” by decades. I really have no idea what you mean. –jacobolus (t) 07:16, 6 February 2010 (UTC)
- That's exactly what Munsell talks about in his books: a representation of gamut in a cylindrical (or sometimes spherical) space. And whereas generally labeling things as color spaces would be appropriate in an article about the Munsell system, it would not be here, except in sections specifically discussing their application to color spaces. SharkD Talk 02:40, 6 February 2010 (UTC)
- That doesn’t make any sense. You’d never try to compare gamuts of two RGB color spaces with respect to the HSV representation of one of them. It would just be a very complicated and arbitrary shape... and either way it has nothing to do with any distinction between “color model” and “color space”. –jacobolus (t) 02:14, 6 February 2010 (UTC)
- As in, mapping the HSL and HSV color models to a particular color space. If you were to place the coordinates with respect to differences in gamut, then the resulting cylinder would be distorted in much the same way as the RGB cube is in the CIELAB images. SharkD Talk 01:55, 6 February 2010 (UTC)
- Huh? I don’t know what “If mapped to a particular color space” means, in this context. If you plotted their colors in, e.g., CIELAB, you’d end up with the same gamut as the plots shown... because it’s the same colors either way, RGB or HSV. –jacobolus (t) 01:02, 6 February 2010 (UTC)
- Yes, that's exactly why I think "color model" should be used. HSL and HSV are transformations of the "overall" RGB model. If mapped to a particular color space, their shapes would look different based on the particular gamut used (such as in the sRGB and Adobe RGB images in the 'Disadvantages' section). Whereas a plot of the models' shapes would always remain the same. SharkD Talk 00:48, 6 February 2010 (UTC)
- Also, I think “color space” is more appropriate, as this depends completely on the particular RGB space in use: each RGB color space implies a different HSL/HSV representation. Whereas “RGB color model” to me indicates the overall idea of RGB. –jacobolus (t) 00:21, 6 February 2010 (UTC)
use "HLS" instead of "HSL"
This template must be substituted.
I've been reading all the papers I can find about these representations, and it seems that "HLS" is used as a name quite a bit more frequently than "HSL", especially in computer graphics literature. Both are very common, and on the web a query for "HLS color" turns up 290k results vs. 240k for "HSL color". So either is probably okay as a name for this article. But we should strive to be as accurate as possible, etc. So unless there are any objections, I'm going to move this article to "HLS and HSV" once I'm finished rewriting it (see previous talk page section). –jacobolus (t) 17:22, 29 January 2010 (UTC)
- There's a "Did you mean to search for: HSL color" message at the bottom of the Google search results. SharkD Talk 00:34, 31 January 2010 (UTC)
- Also, when searching for both search terms, "HLS HSV color" results in 135k hits, while "HSL HSV color" results in 985k hits. SharkD Talk 00:38, 31 January 2010 (UTC)
- I think that HSL is more common now than it once was (probably thanks at least in part to Misplaced Pages!), and especially when both are described people are tempted to mix up the letter order so they’re consistent, but HLS is used in almost all of the scientific papers about the subject, and by other “careful” sources (for instance, the Mac OS 8.0 color chooser which has both HLS and HSV modes, presenters at SIGGRAPH, etc.). I don’t think it’s too big a deal, but Misplaced Pages should strive to be as accurate as possible. –jacobolus (t) 02:05, 1 February 2010 (UTC)
- I guess. Here's a breakdown:
- I think that HSL is more common now than it once was (probably thanks at least in part to Misplaced Pages!), and especially when both are described people are tempted to mix up the letter order so they’re consistent, but HLS is used in almost all of the scientific papers about the subject, and by other “careful” sources (for instance, the Mac OS 8.0 color chooser which has both HLS and HSV modes, presenters at SIGGRAPH, etc.). I don’t think it’s too big a deal, but Misplaced Pages should strive to be as accurate as possible. –jacobolus (t) 02:05, 1 February 2010 (UTC)
Edited several times since the initial posting. Search term "HSL HSV" "HLS HSV" "HSL color" "HLS color" "HSL colour" "HLS colour" "HSL adobe" "HLS adobe" Google Web 1160k 279k 245k 278k 3160k 343k 92k 132k Google Blogs 1856 1166 9435 8680 10690 8680 4370 3422 Google Books 627 636 758 834 804 926 420 313 Google Scholar 1050 1390 6590 11800 6360 20100 742 7690 Google Web (2000 - 2010) unavailable Google Blogs (2000 - 2010) 1809 1153 9229 7585 10473 7884 4276 3062 Google Books (2000 - 2010) 305 332 666 650 674 667 309 245 Google Scholar (2000 - 2010) 524 681 3150 4150 3070 16800 450 3720
- I don't see "almost all of the scientific papers" anywhere in these numbers, or the relevance of the Mac OS color picker as the Windows color picker uses HSL. As far as book authors go, there's not much of a difference in numbers or date of authorship. Not sure what policy is in this regard. Generally, we're supposed to go by what most people are familiar with, for instance "dog" versus "Canis lupus" or "Zoe Saldana" versus "Zoë Saldaña". SharkD Talk 03:12, 2 February 2010 (UTC)
- w/r/t date of authorship, the original dimensions in Joblove and Greenberg (1978) were called "hue", "intensity", and "relative chroma". Then Tektronix introduced the 4027 terminal in 1979, which called it HLS (the only difference from the version described in this article being that blue was placed at 0°). Also in 1979, the Computer Graphics Standards Committee recommended the space, and called it HLS. Following that, every source from the 1970s and early 80s calls it HLS. By the time we get to the 1990s, both terms are in use, but the most authoritative computer graphics textbooks, and papers presented at SIGGRAPH, etc., seem to still almost exclusively use the term HLS. Microsoft’s color picker doesn’t use an abbreviation for this space anywhere, as far as I know: they just label their input boxes. Photoshop also doesn't put the abbreviation anywhere: it just has a "hue/saturation" tool. The real notable number in the chart above is the "HLS color" number from Google Scholar. –jacobolus (t) 03:42, 3 February 2010 (UTC)
- While it would be good to mention it for a historical perspective, I don't think it's necessary to change it in the text. Lots of terminology changes over time. Science and technology aren't static. My remark WRT the dates of authorship was in response to your statement that Misplaced Pages had somehow influenced the term's presence in external texts. The dates are spread fairly well across a wide time frame, leaving this conclusion in doubt. SharkD Talk 10:14, 3 February 2010 (UTC)
- I added a few more rows to the table with additional statistics based on date. Yes, the gap is growing closer, but HLS still seems to be in the lead as far as scholarly works and books are concerned. (I don't have data for Google Web.) As CSS3 takes hold this trend will probably continue. I also requested assistence over at WP:Village pump (policy)#Popular and recent usage, or scholarly and historical usage?, and they should get back to us here. SharkD Talk 10:47, 3 February 2010 (UTC)
- While it would be good to mention it for a historical perspective, I don't think it's necessary to change it in the text. Lots of terminology changes over time. Science and technology aren't static. My remark WRT the dates of authorship was in response to your statement that Misplaced Pages had somehow influenced the term's presence in external texts. The dates are spread fairly well across a wide time frame, leaving this conclusion in doubt. SharkD Talk 10:14, 3 February 2010 (UTC)
- Also, I'm pretty sure that we call her "Zoe Saldana" because that's her name according to the SAG, how she's listed in movie credits, etc. –jacobolus (t) 03:46, 3 February 2010 (UTC)
- Yes, that's my point. It's how we all know her now, not what she was (or may have been) named in the past. (The sources aren't consistent.) SharkD Talk 10:14, 3 February 2010 (UTC)
- One last bit of confusion: Alvy Ray Smith's 1978 paper describes HSV and a "hue"/"saturation"/"brightness" (HSL) model, but what he calls the HSL "triangle model" is quite different from the HSL/HLS that we are describing in this article. –jacobolus (t) 04:15, 3 February 2010 (UTC)
- I would like to see the paper if you happen to have a copy. SharkD Talk 10:14, 3 February 2010 (UTC)
- I can’t find your email address on your user page or homepage. Shoot me an email and I'll happily pass along any of these papers you want to see. –jacobolus (t) 04:40, 4 February 2010 (UTC)
- I would like to see the paper if you happen to have a copy. SharkD Talk 10:14, 3 February 2010 (UTC)
- w/r/t date of authorship, the original dimensions in Joblove and Greenberg (1978) were called "hue", "intensity", and "relative chroma". Then Tektronix introduced the 4027 terminal in 1979, which called it HLS (the only difference from the version described in this article being that blue was placed at 0°). Also in 1979, the Computer Graphics Standards Committee recommended the space, and called it HLS. Following that, every source from the 1970s and early 80s calls it HLS. By the time we get to the 1990s, both terms are in use, but the most authoritative computer graphics textbooks, and papers presented at SIGGRAPH, etc., seem to still almost exclusively use the term HLS. Microsoft’s color picker doesn’t use an abbreviation for this space anywhere, as far as I know: they just label their input boxes. Photoshop also doesn't put the abbreviation anywhere: it just has a "hue/saturation" tool. The real notable number in the chart above is the "HLS color" number from Google Scholar. –jacobolus (t) 03:42, 3 February 2010 (UTC)
- Firstly, don't forget "HSL colour" and "HLS colour". Personally, I have studied computer graphics courses and colour models at masters level, and worked with them for the past year, and have never seen "HLS". OrangeDog (τ • ε) 12:38, 3 February 2010 (UTC)
- OK, I added a column for "HSL colour" and "HLS colour". The Web vs. Scholar schism seems even more pronounced. SharkD Talk 05:52, 4 February 2010 (UTC)
- I think what might have happened is people re-constructed an acronym from looking at the order of Photoshop's hue/saturation tool ("hue", "saturation", "lightness") or MS's color picker ("hue", "sat", "lum"), or from taking the order from HSV (whose use is more common than HLS/HSL in software), rather than from the technical/academic descriptions, and then because those web descriptions were more accessible than journal articles, other people just looking the thing up came more and more to use the "HSL" order, to the point where among all the non-technical vague descriptions that one finds littered around the web, "HSL" has even overtaken "HLS" as the most common order. Not sure where that leaves Misplaced Pages though... I still think we should go for the abbreviation used more often by experts. –jacobolus (t) 10:59, 4 February 2010 (UTC)
- I asked for a third opinion since the village pump didn't result in much comment. SharkD Talk 03:37, 5 February 2010 (UTC)
| Is there any reason we can't simply allow both names to exist by leaving this page named with HSL and creating a redirect from the HLS page. The empirical search results above seem to indicate that (at least among search engines) there is no clear correct name for this. The article already contains a helpful reference to the fact that "HSL is often also called HLS or HSI, and HSV is often also called HSB". I am going to leave the 3O request open because this could probably benefit from more than just my eyes on it. 7 03:46, 5 February 2010 (UTC) |
.
| I also believe that both names should be left. After all it seems clear from above that there is no proper or "official" term. It would help to have both. Perhaps stating which one is most commonly use or recognized. 04:02, 5 February 2010 (UTC)—SoCal L.A. (talk) 04:02, 5 February 2010 (UTC) |
- It affects the name of the article as well. We already have two acronyms in the title. Adding the full selection would be a huge mess. Personally, I am more familiar with HSL, and like the symmetry with respect to HSV. SharkD Talk 04:40, 5 February 2010 (UTC)
- Levkowitz and Herman 1993.
- Wilhelm Ostwald (1916). Die Farbenfibel. Leipzig.
Wilhelm Ostwald (1918). Die Harmonie der Farben. Leipzig. - Gar A. Bergstedt (April 1983). US patent 4694286, “Apparatus and method for modifying displayed color images”. Filed 1983-04-08. Issued 1987-09-15. Assigned to Tektronix, Inc.


















 to make it a bi-cone.
to make it a bi-cone. 


 : The color gets darker, black for
: The color gets darker, black for  and unchanged for
and unchanged for  . This means scaling toward 0.
. This means scaling toward 0.

 : The color gets lighter, white for
: The color gets lighter, white for  and unchanged for
and unchanged for  (i.e. scale 0), the scaling factor is
(i.e. scale 0), the scaling factor is  (and not
(and not  ).
).
