This is an old revision of this page, as edited by 203.200.95.130 (talk) at 15:46, 21 June 2004. The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.
Revision as of 15:46, 21 June 2004 by 203.200.95.130 (talk)(diff) ← Previous revision | Latest revision (diff) | Newer revision → (diff)- This article is about an engineering theory called control theory. There is also a sociological theory of deviant behavior that is also called control theory.
In engineering and mathematics, control theory deals with the behaviour of dynamical systems over time. The desired output of a system is called the reference variable. When one or more output variables of a system need to show a certain behaviour over time, a controller tries to manipulate the inputs of the system to realize this behaviour at the output of the system.
An example
As an example, consider cruise control. In this case, the system is a car. The goal of the cruise control is to keep it at a constant speed. So, the output variable of the system is the speed of the car. The primary means to control the speed of the car is the amount of gas being fed into the engine.
A simple way to implement cruise control is to lock the position of the gas pedal the moment the driver engages cruise control. This is fine if the car is driving on perfectly flat terrain. On hilly terrain, the car will accelerate when going downhill and slow down when going uphill; something its driver may find highly undesirable.
This type of controller is called an open-loop controller because there is no direct connection between the output of the system and its input. One of the main disadvantages of this type of controller is the sensitivity to the dynamics of the system under control.
Classical control theory
To avoid the problems of the open-loop controller, control theory introduces feedback. The output of the system y is fed back to the reference value r. The controller C then takes the difference between the reference and the output, the error e, to change the inputs u to the system under control P. This is shown in the figure. This kind of controller is a closed-loop controller or feedback controller.
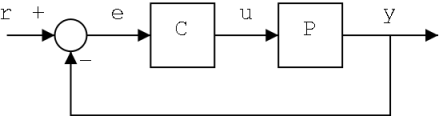
A simple feedback control loop
If we assume the controller C and the plant P are linear, time-invariant and all single input, single output, we can analyse the system above by using the Laplace transform on the variables. This gives us the following relations:
Solving for Y(s) in terms of R(s), we obtain:
The term PC/(1 + PC) is referred to as the transfer function of the system.
If we can ensure PC >> 1, then Y(s) is approximately equal to R(s).
This means we control the output by simply setting the reference.
State space representation
To get a coherent model for systems with multiple inputs and multiple outputs, we need a way to record every relation between any input variable and any output variable. With n inputs and m outputs, we have to write down mn Laplace transforms to encode all the information about a system. A more compact representation of a system is its state space representation using p internal states:
where
- .
For simplicity, D is often chosen to be the zero matrix.
The internal states are stored in the x(t) vector
Note: The internal state variables may not be physically measureable quantities. These variables do not represent real physical quantities, they are merely variables chosen to best represent the system as a whole.
- is the input vector
- is the output vector
After applying the Laplace transform, this representation takes the form:
The characteristic polynomial of the state space representation is:
Simple example of state space representation
Let's take the simplest possible example of the state space representation. Here we have a single input variable and a single output variable. Also the internal state of the system is only represented by a single variable.
- y(t) is the output variable
- u(t) is the input variable
- x(t) is the internal state variable
Here, the output y(t) is the result of a linear addition of the internal state x(t) with the linear addition of value of the input u(t)
The internal state can have the following relationship with the input.
Putting everything together, we have
Controllability and observability
Controllability is a measure for the ability to use a system's external inputs to manipulate its internal state. Observability is a measure for how well internal states of a system can be inferred by knowledge of its external outputs. The observability and controllability of a system are mathematical duals.
See also
- Control engineering
- process control
- robotic unicycle
- H infinity
- Optimal control
- Servo
- Non-linear control
- Adaptive control
- Intelligent Control










 .
.
 is the input vector
is the input vector is the output vector
is the output vector




