This is an old revision of this page, as edited by Incnis Mrsi (talk | contribs) at 11:15, 28 July 2012 (a proper disambiguation, cleansing after contaminations by user:Globbet and user:Jonah22). The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.
Revision as of 11:15, 28 July 2012 by Incnis Mrsi (talk | contribs) (a proper disambiguation, cleansing after contaminations by user:Globbet and user:Jonah22)(diff) ← Previous revision | Latest revision (diff) | Newer revision → (diff) This article is about Earth's and planets' nutation. For other uses, see Nutation (disambiguation).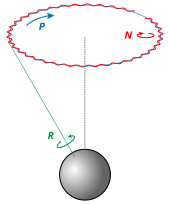
Nutation (from Latin: nūtāre, to nod) is a rocking, swaying, or nodding motion in the axis of rotation of a largely axially symmetric object, such as a gyroscope, planet, or bullet in flight, or as an intended behavior of a mechanism. A pure nutation is a movement of a rotational axis such that the first Euler angle (precession) is constant.
The nutation of a planet happens because of tidal forces that cause the precession of the equinoxes to vary over time so that the speed of precession is not constant. The nutation of the axis of the Earth was discovered in 1728 by the British astronomer James Bradley, but this nutation was not explained in detail until 20 years later.
Because the dynamic motions of the planets are so well-known, their nutations can be calculated to within arcseconds over periods of many decades. There is another disturbance of the Earth's rotation called polar motion that can be estimated for only a few months into the future because it is influenced by rapidly and unpredictably varying things such as ocean currents, wind systems, and motions in the liquid nickel-iron core of the Earth.
Values of nutations are usually divided into components parallel and perpendicular to the ecliptic. The component that works along the ecliptic is known as the nutation in longitude. The component perpendicular to the ecliptic is known as the nutation in obliquity. Celestial coordinate systems are based on an "equator" and "equinox," which means a great circle in the sky that is the projection of the Earth's equator outwards, and a line, the Vernal equinox intersecting that circle, which determines the starting point for measurement of right ascension. These items are affected both by precession of the equinoxes and nutation, and thus depend on the theories applied to precession and nutation, and on the date used as a reference date for the coordinate system. In simpler terms, nutation (and precession) values are important in observation from Earth for calculating the apparent positions of astronomical objects.
Earth

In the case of the Earth, the principal sources of tidal force are the Sun and Moon, which continuously change location relative to each other and thus cause nutation in Earth's axis. The largest component of Earth's nutation has a period of 18.6 years, the same as that of the precession of the Moon's orbital nodes. However, there are other significant periodical terms that must be calculated depending on the desired accuracy of the result. A mathematical description (set of equations) that represents nutation is called a "theory of nutation" (see, e.g., ). In the theory, parameters are adjusted in a more or less ad hoc method to obtain the best fit to data. As can be seen from the IERS publication just cited, nowadays simple rigid-body mechanics do not give the best theory; one has to account for deformations of the solid Earth.
Values
The principal term of nutation is due to the regression of the moon's nodal line and has the same period of 6798 days (18.6 years). It reaches plus or minus 17″ in longitude and 9″ in obliquity. All other terms are much smaller; the next-largest, with a period of 183 days (0.5 year), has amplitudes 1.3″ and 0.6″ respectively. The periods of all terms larger than 0.0001″ (about as accurately as one can measure) lie between 5.5 and 6798 days; for some reason they seem to avoid the range from 34.8 to 91 days, so it is customary to split the nutation into long-period and short-period terms. The long-period terms are calculated and mentioned in the almanacs, while the additional correction due to the short-period terms is usually taken from a table.