Misplaced Pages

This is an old revision of this page, as edited by DVdm (talk | contribs) at 14:41, 3 June 2013 (→A trivial refutation of one of Dingle's Fumbles (Ref: Talk:Herbert Dingle Archive): Darkened math colour to DarkGreen). The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.

This... This user has been on Misplaced Pages for 19 years and 8 months. This user listens to Frank Zappa. vn-82 This user page has been vandalized 82 times.

A trivial refutation of one of Dingle's Fumbles (Ref: Talk:Herbert Dingle Archive)

On page 230 in this appendix to "Science At the Crossroads", Dingle writes:

(start quote)

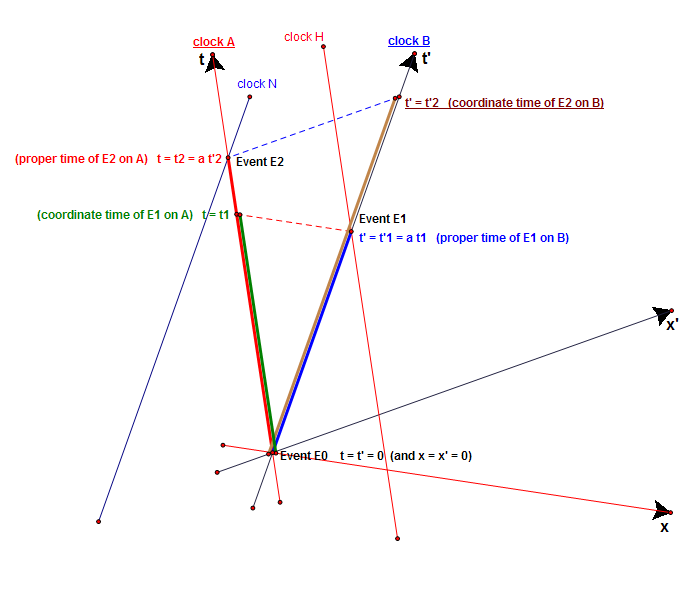
Thus, between events E0 and E1, A advances by ${\displaystyle \color {DarkGreen}{t_{1}}}$ and B by ${\displaystyle \color {Blue}{t'_{1}=at_{1}}}$ by (1). Therefore

${\displaystyle {\frac {\color {DarkGreen}{\text{rate of A}}}{\color {Blue}{\text{rate of B}}}}={\frac {\color {DarkGreen}{t_{1}}}{\color {Blue}{at_{1}}}}={\frac {1}{a}}>1\qquad {\text{(3)}}}$

...

Thus, between events E0 and E2, B advances by ${\displaystyle \color {Brown}{t'_{2}}}$ and A by ${\displaystyle \color {Red}{t_{2}=at'_{2}}}$ by (2). Therefore

${\displaystyle {\frac {\color {Red}{\text{rate of A}}}{\color {Brown}{\text{rate of B}}}}={\frac {\color {Red}{at'_{2}}}{\color {Brown}{t'_{2}}}}=a<1\qquad {\text{(4)}}}$

Equations (3) and (4) are contradictory: hence the theory requiring them must be false.

(end quote)

Dingle should have written as follows:

(start correction)

Thus, between events E0 and E1, A, which is not present at both events, advances by ${\displaystyle \color {DarkGreen}{t_{1}}}$ and B, which is present at both events, by ${\displaystyle \color {Blue}{t'_{1}=at_{1}}}$ by (1). Therefore

Failed to parse (syntax error): {\displaystyle \frac{\color{DirkGreen}{\text{rate of clock not present at both events E0 and E1}}}{\color{Blue}{\text{rate of clock present at both events E0 and E1}}} = \frac{\color{<<DarkGreen}{\text{coordinate time of E1}}}{\color{Blue}{\text{proper time of E1}}} = \frac{\color{DarkGreen}{\text{rate of A}}}{\color{Blue}{\text{rate of B}}} = \frac{\color{DirkGreen}{t_1}}{\color{Blue}{t'_1}} = \frac{\color{DarkGreen}{t_1}}{\color{Blue}{a t_1}} = \frac{1}{a} > 1 \qquad \text{(3)}}

...

Thus, between events E0 and E2, B, which is not present at both events, advances by ${\displaystyle \color {Brown}{t'_{2}}}$ and A, which is present at both events, by ${\displaystyle \color {Red}{t_{2}=at'_{2}}}$ by (2). Therefore

${\displaystyle {\frac {\color {Brown}{\text{rate of clock not present at both events E0 and E2}}}{\color {Red}{\text{rate of clock present at both events E0 and E2}}}}={\frac {\color {Brown}{\text{coordinate time of E2}}}{\color {Red}{\text{proper time of E2}}}}={\frac {\color {Brown}{\text{rate of B}}}{\color {Red}{\text{rate of A}}}}={\frac {\color {Brown}{t'_{2}}}{\color {Red}{t_{2}}}}={\frac {\color {Brown}{t'_{2}}}{\color {Red}{at'_{2}}}}={\frac {1}{a}}>1\qquad {\text{(4)}}}$

Equations (3) and (4) are consistent and say that any event's coordinate time is always larger than its proper time:

hence there is no reason to say that the theory requiring them must be false.

(end correction)

DVdm 12:18, 6 August 2007 (UTC)