This is an old revision of this page, as edited by David Eppstein (talk | contribs) at 20:24, 23 June 2013 (→Wondering why you un-PROD-ded Hayford Peirce: r). The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.
Revision as of 20:24, 23 June 2013 by David Eppstein (talk | contribs) (→Wondering why you un-PROD-ded Hayford Peirce: r)(diff) ← Previous revision | Latest revision (diff) | Newer revision → (diff)|
Archives |
|
2009a, 2009b, 2009c, 2009d, 2009e 2010a, 2010b, 2010c, 2010d 2011a, 2011b, 2011c, 2011d 2012a, 2012b, 2012c, 2012d 2013a |
Hi, and welcome to my User Talk page! For new discussions, I prefer you add your comments at the very bottom and use a section heading (e.g., by using the "New section" tab at the top of this page). I will respond on this page unless specifically requested otherwise.
No article on the dimension of a graph
Hi David,
I noticed English Misplaced Pages has articles on the metric dimension of a graph, or on the biclique dimension of a graph, but nothing on the notion described in Erd ̋os, P., Harary, F. and Tutte, W. T., On the dimension of a graph, Mathematika 12, 1965, pages 118–122.
They define it as the minimum number such that a graph can be embedded in the n-dimensional Euclidean space with every edge of being a segment of length 1.
Is the lack of an article on this topic intentional? The closest thing I have been able to find was the notion of dimension of a simplex, which is the geometrical equivalent in the special case of the complete graphs.
Best, --MathsPoetry (talk) 12:09, 20 March 2013 (UTC)
- It's not an intentional omission, but it is mentioned in Unit distance graph#Generalization to higher dimensions.
- OK, missed that one, thanks. And would it be worth an article, according to you? Alexander Soifer dedicates a whole chapter to that in his 2009 book "The Mathematical Coloring Book" (Springer). --MathsPoetry (talk) 16:35, 20 March 2013 (UTC)
- Sure, that sounds like plenty of material for an article. You could call it Euclidean dimension, maybe? —David Eppstein (talk) 16:46, 20 March 2013 (UTC)
- Okay, I will write it (in French Wikipédia), starting on tomorrow. I indeed have a lot of matter for it.
- My first intention was also to call it "Euclidian dimension" to distinguish it from "metric dimension' or "bipartite dimension", but:
- it would be "own work" of mine
- worse, Soifer introduces "Euclidian dimension" for a slightly different concept (which other people call "faithful dimension"), and which I intend to describe on the same page.
- So I think it will simply be "graph dimension" or "dimension (graph theory)". I agree it is suboptimal and it also bothers me. --MathsPoetry (talk) 17:05, 20 March 2013 (UTC)
- Sure, that sounds like plenty of material for an article. You could call it Euclidean dimension, maybe? —David Eppstein (talk) 16:46, 20 March 2013 (UTC)
- OK, missed that one, thanks. And would it be worth an article, according to you? Alexander Soifer dedicates a whole chapter to that in his 2009 book "The Mathematical Coloring Book" (Springer). --MathsPoetry (talk) 16:35, 20 March 2013 (UTC)
![]() Done, see fr:Dimension (théorie des graphes). I tried to remain entry-level, and to focus on the most important aspects. Feel free to reuse the images I had to create to illustrate this article. --MathsPoetry (talk) 18:30, 21 March 2013 (UTC)
Done, see fr:Dimension (théorie des graphes). I tried to remain entry-level, and to focus on the most important aspects. Feel free to reuse the images I had to create to illustrate this article. --MathsPoetry (talk) 18:30, 21 March 2013 (UTC)
- I have started to translate it into English, my work-in-progress is at User:Maproom/Dimension_(graph_theory). Maproom (talk) 21:43, 21 April 2013 (UTC)
- The French article uses templates with the names "démonstration" and "Théorème". If en:Misplaced Pages has equivalent templates (which seem to me an excellent device) I have failed to find them. What would you advise? My attempt to use {{Proof|state=collapsed}} did not have the result I had hoped for :-)
Template:Math proof Error caused by a symbol in proof: use proof parameter
Maproom (talk) 19:09, 22 April 2013 (UTC)
Andrew Gleason
Thanks for the work on this article. I still say to myself when I am depressed and find myself forced to listen to pompous and tiresome people "Well, I have known something you have never known, and that is the pleasure of dining and conversing with Gleason hundreds of times over many years, on something like equal terms, and to have been his friend."
I never got around to asking him what exactly he was doing in Berkeley. If you know, can you clarify that in the article?
EEng (talk) 12:17, 4 April 2013 (UTC)
- Unfortunately the book I used doesn't say why, it just says his family lived there for a semester, in spring 1936. He also tells a story from that time of regularly taking a trolley to the Chabot Observatory, and at some point buying a telescope to stargaze, but then back in Bronxville only being able to do so when it was too cold for comfort, and giving it up for that reason. —David Eppstein (talk) 16:13, 4 April 2013 (UTC)
- That's good enough, actually. Please keep an eye on my further edits (which may or may not be substantial in the immediate future, depending...) and, if you are amenable let's prod each other to further efforts periodically. I'm guessing from your CV that you probably never met him, but as you must have gathered he was a just plain extraordinary person as well as an extraordinary mathematician, and he deserves a much better article. Notice I've started citing the AMS appreciation, which is wonderful. EEng (talk) 16:40, 4 April 2013 (UTC)
- What the article is really missing is a discussion of his mathematical accomplishments. If we can cover that part, with about the same amount of text as the biographical material, and within a few days, we might be able to meet the 5x expansion requirements for WP:DYK. (It needs to be a 5x expansion of the prose of the article, not counting lists (like the previous list of publications) but also not counting block quotes.) —David Eppstein (talk) 17:50, 4 April 2013 (UTC)
- That's good enough, actually. Please keep an eye on my further edits (which may or may not be substantial in the immediate future, depending...) and, if you are amenable let's prod each other to further efforts periodically. I'm guessing from your CV that you probably never met him, but as you must have gathered he was a just plain extraordinary person as well as an extraordinary mathematician, and he deserves a much better article. Notice I've started citing the AMS appreciation, which is wonderful. EEng (talk) 16:40, 4 April 2013 (UTC)
Never thought of DYK -- isn't there a timespan within which the expansion must be completed? Hmmm.. what would be the fun fact -- his continuing cipher and security work no one knew abuot? The no-PhD bit (though that isn't, or at least wasn't, completely unheard of)? Wait... lots more is coming to mind. Oh goody. Let's do it!
But if it's gonna get main-page exposure the bio needs to be really tops. You mentioned his research as needing fleshing out but there are at least three areas that IMO we should be sure to cover /well/:
- research (as you mentioned)
- teaching (both his own + leadership in reforming/improving math teaching -- for a few years he spent one day a week with grade school kids trying out different ways of presenting concepts, and hearing how kids think about math and struggle through problems -- that might be a good DYK too)
- cipher work
This leaves out service to Harvard and learned societies, no doubt much Society of Fellows stuff, any number of worthwhile anecdotes (e.g. personally guarding (with other trusted faculty) Widener Library for several nights after a firebomb threat in the 60s -- I had that story from him but haven't run into it in sources yet; guessing the combination to an officer's safe when he was in the Navy; etc.) -- these and more (in yet other categories) are harder to source so we can only do our best.
Hope you don't fear I'm turning this into a giant project but I do hope we can do him justice. Since I'm in CS/Stat, not hard math, if you'll take the lead on his research I'll be happy to take the lead on the rest.
EEng (talk) 22:28, 4 April 2013 (UTC)
P.S. I figured you'd recognize the Hardy allusion in my first post above, but on the off chance you don't please follow the link so you won't think I'm strange.
- It's a pretty short deadline: five days from the start of expansion on April 3. DYK also has somewhat strict standards for sourcing: every paragraph (outside the lead section) needs at least one footnote. And unfortunately the timing is inconvenient for me: I'm traveling starting April 6, and likely to be incommunicado from the morning of the 6th (Pacific time) until the evening of the 7th (European central time). My own mathematical interests are separate enough that understanding his contributions is going to take some effort — Ramsey theory I understand well, but not so much the rest. But I'll see if I can find some time to work on it. As for Hardy, I didn't actually recognize the quote, so thanks for the link. —David Eppstein (talk) 23:43, 4 April 2013 (UTC)
- I've thought about what a mathematical biography aimed at laymen should try to do. My philosophy: give a layman a glimpse of what a mathematician does -- illustrated by what this mathematician did in at least one area. Hopefully there's enough technical detail to suggest to a math grad student where Gleason's work fits into the student's knowledge of the subject, but that's not as important as the text serving the layman -- there's a separate article on H5th for that (whether it's any good at the moment isn't our problem). So I envisage something like the following. (Please remember that while I may have understood this material in some vague way decades ago, I've completely made this up out of my head after just glancing at p.1245 of the AMS Notices bio, left column. I hope it doesn't make me seem too much like an idiot, nor that I'm prescribing what you should do. It's just to give the flavor I envisage.)
- AG is probably best known for his work on Hilbert's Fifth Problem, which concerns Lie groups. A large amount of work had been done on Lie groups, exploring their structure and their relationship to other mathematical ideas, such as /list/. However, much of this work assumed "formal statement of undesirable assumption" -- essentially, assuming /layman's analogy of assumption/ -- and H5thP asked whether the same results still held without that assumption. Gleason contributed two of the handful of critical steps in resolving this question, one in his 1949 "Title of paper", and the other in his 1952 "Other paper", which combined his earlier result with those of others who had published in the interim, to reach a much stronger etc etc.
- Gleason's two steps might understood by the following analogies. ///At this point if you're highly inspired you might be able to come up with something really effective here. But if not, OK, leave it out.///
- Soon after, Person X published essentially a final resolution of the question in a paper which used this stronger result to do this and that or something something or other. Since Lie groups are important in //impressive list of areas//, this was an important result, and its importance has increased over the years as applications in //further list// have been developed.
- I've thought about what a mathematical biography aimed at laymen should try to do. My philosophy: give a layman a glimpse of what a mathematician does -- illustrated by what this mathematician did in at least one area. Hopefully there's enough technical detail to suggest to a math grad student where Gleason's work fits into the student's knowledge of the subject, but that's not as important as the text serving the layman -- there's a separate article on H5th for that (whether it's any good at the moment isn't our problem). So I envisage something like the following. (Please remember that while I may have understood this material in some vague way decades ago, I've completely made this up out of my head after just glancing at p.1245 of the AMS Notices bio, left column. I hope it doesn't make me seem too much like an idiot, nor that I'm prescribing what you should do. It's just to give the flavor I envisage.)
- If the article had something like the above, plus a paragraph consisting of heavily linked one-sentence nods to each of his other major research areas, that would be absolutely fine to appear on main page. Or if even that's too much, just the paragraph of one-sentence nods -- there's only one chance for DYK on this (right?) and we should take it. I hope this doesn't make you regret having suggested it.
- However, my impression is that once the DYK nomination is in place at the end of the 5 days, there can be quite long periods of discussion about hooks and so on, and this would give time for further improvement.
- I'll take care of everything else, with priority to #2 and #3 in my list from my earlier post.
- So, whatcha think? Can we do it?
- EEng (talk) 02:15, 5 April 2013 (UTC)
- It does look within reach to me. In the meantime I've made some progress on understanding the 5th problem, so that's the part I was intending to work on next. —David Eppstein (talk) 04:03, 5 April 2013 (UTC)
- Ok, Hilbert done. By my count we've already reached the 5x expansion, but we can't nominate for DYK until it looks like a finished article; in particular, the "expand me" template in the Gleason's theorem section needs to be replaced by actual text. It's probably not too early to start thinking about DYK hooks; do you have any ideas for that? —David Eppstein (talk) 05:23, 5 April 2013 (UTC)
- See article Talk for hooks. I think you're overstating finished-ness requirement for DYK. From what I can see incredible crap is allowed through -- they seem to case only about superficial stuff like length, no s, no redlinks (?), MOS. I think no one will care if who subtopics are missing or inadequately treated (not that we want it that way). Again -- I think there's at least a few days' delay before article goes live on main page, during which additional work can be done. Here are some DYK links I found:
- WP:Did_you_know/Supplementary_guidelines
- WP:Did you know which btw says D7: There is a reasonable expectation that an article—even a short one—that is to appear on the front page should appear to be complete and not some sort of work in progress. Therefore, articles which include unexpanded headers are likely to be rejected. Articles that fail to deal adequately with the topic are also likely to be rejected. For example, an article about a book that fails to summarize the book's contents, but contains only a bio of the author and some critics' views, is likely to be rejected as insufficiently comprehensive. That's pretty weak.
- .
- EEng (talk) 06:45, 5 April 2013 (UTC)
- See article Talk for hooks. I think you're overstating finished-ness requirement for DYK. From what I can see incredible crap is allowed through -- they seem to case only about superficial stuff like length, no s, no redlinks (?), MOS. I think no one will care if who subtopics are missing or inadequately treated (not that we want it that way). Again -- I think there's at least a few days' delay before article goes live on main page, during which additional work can be done. Here are some DYK links I found:
- Ok, Hilbert done. By my count we've already reached the 5x expansion, but we can't nominate for DYK until it looks like a finished article; in particular, the "expand me" template in the Gleason's theorem section needs to be replaced by actual text. It's probably not too early to start thinking about DYK hooks; do you have any ideas for that? —David Eppstein (talk) 05:23, 5 April 2013 (UTC)
- It does look within reach to me. In the meantime I've made some progress on understanding the 5th problem, so that's the part I was intending to work on next. —David Eppstein (talk) 04:03, 5 April 2013 (UTC)
Sure, but right now the article does contain an unexpanded header, one of the things it warns against. —David Eppstein (talk) 06:56, 5 April 2013 (UTC)
- But my experience, limited as it is, is that no one at DYK cares if you just throw out all the s and please-expand templates and stuff -- the things which move article development forward -- as long as it doesn't make it obvious that the article is incomplete. I had a very unpleasant experience with an editor who, because he had a DYK nomination in, wanted certainly-true but momentarily material purged so it wouldn't hold up his DYK nominator . I believe DYK's the 5-day rush, and its article-quality criteria -- quite different from those for GA and FA -- which emphasize superficial stuff like "can't have ", combine to encourage the creation of "Potemkin" articles which pretend to be much more finished than they are. Some of them are downright embarrassing.
- Anyway, if time runs out any remaining research topics can be replaced by one-sentence summaries -- no one at DYK will care. It's a real shame, though, because the exposure from being on the main page should be an opportunity for people to see needs-improvement templates, , and so on, and jump in to help. DYK's criteria militate in the exact opposite direction.
- Great work you've been doing on this. See hook thoughts at Talk:Andrew Gleason.
- EEng (talk) 16:49, 5 April 2013 (UTC)
- Thanks. Sometimes DYK does work in the way you think it should: I've been seeing significant improvements on Tubutulik River (one of the nominations I reviewed before putting in my own most recent one) after its DYK yesterday. —David Eppstein (talk) 16:53, 5 April 2013 (UTC)
AG nominated
Template:Did_you_know_nominations/Andrew_Gleason EEng (talk) 06:34, 7 April 2013 (UTC)
DYK for Lipman Bers
| On 6 April 2013, Did you know? was updated with a fact from the article Lipman Bers, which you created or substantially expanded. The nomination discussion and review may be seen at Template:Did you know nominations/Lipman Bers. You are welcome to check how many hits the article got while on the front page (here's how, quick check) and it will be added to DYKSTATS if it got over 5,000. If you know of another interesting fact from a recently created article, then please suggest it on the Did you know? talk page. |
Materialscientist (talk) 00:40, 6 April 2013 (UTC)
Not alone anymore
EEng (talk) 03:14, 8 April 2013 (UTC)
- She's a UCI student doing quantum mechanics whom I asked to check the Gleason section. She tells me it looks good. —David Eppstein (talk) 03:21, 8 April 2013 (UTC)
- Should have guessed. I've had a personal distraction but I've got a lot of good material on teaching and personal, but it still needs distilling. Luckily it looks like DYK is way backed up. Good news: looks somewhat positive on getting a photo from Harvard. EEng (talk) 07:33, 10 April 2013 (UTC)
Topological graph theory and theory of topological graphs
Hi David, If you have an opinion on this it would be appreciated. Thanks. Brendan. McKay (talk) 05:14, 11 April 2013 (UTC)
Regards to Delta function
Hey,
I just wanted to say no worries. These situations can a bit confusing to follow sometimes, especially if the discussions are happening on a WikiProject talk page, as opposed to the talk page of the article itself. Anyways, I saw you reverted all of the edits; I was about to do it myself, but you beat me to it. Anyways, I apologize if this caused unnecessary frustration. Cheers! Steel1943 (talk) 23:46, 16 April 2013 (UTC)
San Diego Comic-Con International meetup proposal
![]() You are invited to join the discussion at Misplaced Pages talk:Meetup/LA/SDCC1. RightCowLeftCoast (talk) 17:58, 18 April 2013 (UTC)Template:Z48
You are invited to join the discussion at Misplaced Pages talk:Meetup/LA/SDCC1. RightCowLeftCoast (talk) 17:58, 18 April 2013 (UTC)Template:Z48
Alison Miller
You commented in this afd. The article has just be re-created with additional material, and I therefore declined a G4. You may want to have a look at it--and perhaps add some citation data. . You're the expert I trust for this subject DGG ( talk ) 20:58, 20 April 2013 (UTC)
- She has four papers in MathSciNet, one of which has a surprisingly high number of citations in Google scholar for something so recent (15 for "Arithmetic traces of non-holomorphic modular invariants"), and another of which ("Asymptotic bounds for permutations containing many different patterns") happens to be one of the main references for an active research project of mine. But I think it's still too early to write anything in the article about her research or the citation data for it. —David Eppstein (talk) 21:11, 20 April 2013 (UTC)
A question
I could have asked these on the Reference Desk but I preferred asking it to you instead. I am a high school guy interested in Mathematics and Computer Science. My question:
- Programming competitions like International Olympiad in Informatics
tend to emphasise more on algorithms. Is Algorithms the most important field in Computer Science. Major books on algorithms include Introduction to Algorithms and The Art of Computer Programming. Which books are taught after anyone has mastered them and what topics are taught when anyone has mastered algorithms. Thanks in advance. Solomon7968 (talk) 19:14, 21 April 2013 (UTC)
- Nobody knows what is taught after The Art of Computer Programming has been mastered, because no one have ever mastered it -- for one thing we're all still waiting for the other 14 volumes. EEng (talk) 19:25, 21 April 2013 (UTC)
- The study of algorithms and data structures is one of the more fundamental areas of computer science (you can't do much else without them) but that's not the same as being important. Many areas are important in different ways. As for "what is taught afterwards", in my department curriculum we have a required algorithms class that is not too different from the set of topics in Introduction to Algorithms (although I don't use that book — it teaches the subject in a way that makes it seem like an obscure branch of pure mathematics, divorced from actual programming), following which we have several electives on topics like graph algorithms and computational geometry. The course I'm currently teaching is data structures at a graduate level, with the assumption that our incoming graduate students are already familiar with algorithms as taught in the undergraduate curriculum. Even those classes only cover the basics of their subtopics; there is too much for any one person to master everything. —David Eppstein (talk) 19:38, 21 April 2013 (UTC)
- Thanks very much. The contents of Computer Science in itself is confusing to me. I am from India and we have weekly one or two Computer Science classes but all in field like Microsoft Office and Microsoft Word although BASIC is also taught. It is very inspiring then to hear advice from professional Computer scientists. Solomon7968 (talk) 19:53, 21 April 2013 (UTC)
Shame!
You're putting me to shame. I was hoping to get ahold of the festschrift Glimpses mentioned in the AMS Notices, but suddenly I find myself in S. America for two+ weeks. Meanwhile, I'm stalled on getting a photo, which I really had my heart set on -- but all potential sources are in the Boston area, where as you know things have been a bit hectic lately. In fact I was literally boarding the plane at the moment of truth. It's a weird feeling...by the time I get back probably all trace will be gone, like it never happened, even though I live just 500 yards away. Anyway, great work you're doing. I think I can scrounge a section on Teaching from the AMS material, schedule permitting. Now that things are moving again (do you have DYK nom watchlisted?) how much time do you think we have? EEng (talk) 20:53, 21 April 2013 (UTC)
- Yes, it's watchlisted. Given the review, we may have to come up with a hook that more closely reflects his specific accomplishments. —David Eppstein (talk) 20:57, 21 April 2013 (UTC)
- I don't want to clutter the discussion there too much, but a problem with ALTS mentioning G-G graph is that Greenwood-Gleason graph redirects to Clebsch graph, which takes a lot of the oomph out of the whole thing, don't you think? One thought is to not link Greenwood-Gleason graph in the hook, but can we just agree to go back to ALT1, since as it turns out our friend didn't object to it? EEng (talk) 22:42, 21 April 2013 (UTC)
- The problem with ALT1 is that the usual DYK rules don't tend to allow images that aren't in the article, and that image doesn't have much to do with the content of the article. So if you want to insist on ALT1, you're probably going to have to give up on using an image (unless we can acquire one of Gleason himself). In the meantime continuing to discuss the issue on the nomination page is likely to draw out the nomination process, which looked like it was about to finish; is that what you want? —David Eppstein (talk) 23:01, 21 April 2013 (UTC)
- I don't want to clutter the discussion there too much, but a problem with ALTS mentioning G-G graph is that Greenwood-Gleason graph redirects to Clebsch graph, which takes a lot of the oomph out of the whole thing, don't you think? One thought is to not link Greenwood-Gleason graph in the hook, but can we just agree to go back to ALT1, since as it turns out our friend didn't object to it? EEng (talk) 22:42, 21 April 2013 (UTC)
Gleason photos!
Great news! I just heard back from JB Gleason. Re the photos in Notices credited to her (all but 2 or 3) she writes, "I do hold the rights as noted in the article and do grant permission to include them in Misplaced Pages" -- though there may be a snag wrt to the Navy uniform one -- details later. Anyway, I'm reading up now on how to handle this with OTRS, but I see you're active now so I wanted to catch you -- maybe you know how to handle this. Can I upload the photos and fwd her email to OTRS? Or does she need to send an email directly? Only if you happen to know. Isn't this grand? EEng (talk) 00:01, 24 April 2013 (UTC)
- I think the procedural details of verifying that permission has been granted are less important than exactly what permission was granted. It's not enough to grant permission for the photos to be used in Misplaced Pages. They have to be given an appropriately open license — either CC-BY-SA or something even less restrictive, that would allow not just Misplaced Pages but anyone else to use them on the same terms. See Misplaced Pages:Requesting copyright permission. —David Eppstein (talk) 00:06, 24 April 2013 (UTC)
- Yes, I had decided to omit the 3x5-commons-left-upside-down-backcover-Antartica-release details until I established contact, then somehow forgot just now that her words above wouldn't be enough. In the meantime I've looked at procedures and what's clear (I think) is that I can go ahead and upload, tag OTRS-to-come, and add the images to the article. I'll give her instructions on how she can email formalities tmw to OTRS (they're backlogged 100 days anyway).
- Something else: in addition to the Notices photos I would dearly like to include this, copyright Harvard, and they're being quite stuffy about releasing it (with them I gave the CC lecture and they don't seem to know what I'm talking about, which suggests I haven't got to the right person). So I'm thinking a fair-use argument can be made. Some of the text I'm developing on "Teaching" (and I'll have to hurry) is about his great accessibility, office door open all the time, etc. -- there's a great passage about this in Notices. Well, this photo captures that uniquely, don't you think? The quiet giant in his cluttered office? Uniquely enhances the reader's understanding of this facet of that man? That seems reasonable to you, no? EEng (talk) 00:29, 24 April 2013 (UTC)
- I don't know, it just looks like a portrait of someone in an office to me — it doesn't convey that he is a mathematician or even an academic. I think fair use would have to rest on the argument that no free image of the subject can be found, not on any unique qualities of this image. —David Eppstein (talk) 00:44, 24 April 2013 (UTC)
- Who asked you anyway, you wet blanket!
- Seriously, I've been looking around and arguments not too different from this do fly. We shall see. EEng (talk) 00:57, 24 April 2013 (UTC)
- I don't know, it just looks like a portrait of someone in an office to me — it doesn't convey that he is a mathematician or even an academic. I think fair use would have to rest on the argument that no free image of the subject can be found, not on any unique qualities of this image. —David Eppstein (talk) 00:44, 24 April 2013 (UTC)
DYK for Andrew Gleason
| On 25 April 2013, Did you know? was updated with a fact from the article Andrew Gleason, which you created or substantially expanded. The fact was ... that mathematician Andrew Gleason liked to say that proofs (example pictured) "really aren't there to convince you that something is true—they're there to show you why it is true"? The nomination discussion and review may be seen at Template:Did you know nominations/Andrew Gleason. You are welcome to check how many hits the article got while on the front page (here's how, quick check) and it will be added to DYKSTATS if it got over 5,000. If you know of another interesting fact from a recently created article, then please suggest it on the Did you know? talk page. |
Casliber (talk · contribs) 16:02, 25 April 2013 (UTC)
1. Um, is it my imagination or are your edit summaries beginning to get testy? If I've offended please tell me, and I apologize in advance.
2. As to the gross formatting hack, it looks OK to me in IE and Chrome, and I'm concerned because I've used this syntax in another article for some time. Can you check whether your config also has this problem in Phineas Gage? And if not, can you do a further check, please? In Gage, the actual syntax is
- __TOC__<!--comment at this point (not that it should matter but you never know)-->
- {{clear}}
but in Gleason I used
- __TOC__{{clear}}
-- all on one line (which my better judgment told me not to do but it looked OK in IE so I threw caution to the wind). Is it only the one-line syntax that fails, or both, or what?
3. re Calculus Consortium, please know that I didn't intend an all-positive one-sidedness, but I was running out of time and I couldn't leave it out completely. I always rest easy knowing that you will keep things honest.
EEng (talk) 23:55, 25 April 2013 (UTC)
- In Phineas Gage, in the machine I am currently viewing this on, the text of the lead section extends to about the bottom of Gage's portrait. About 2/3 of a screenfull of space in the main article text is then blank, covering the remaining length of the infobox and the block quote. It looks really ugly. If it makes a difference, I'm viewing this in Chrome, on a Mac, with a monitor that's 1920 pixels wide and a browser window that covers most of that width, using the monobook skin in my Appearance preferences, with some custom CSS that makes the fonts a bit bigger, and with tables of contents disabled (I never see them). In general, my philosophy for this sort of thing is to do as little manual formatting of things as possible, and let the system's default formatting handle it; it's probably much better optimized for many different browsers, many different preference settings, and many different screen sizes than your manual formatting is likely to be. As for any testiness, sorry if that offended (although I get the impression you have thick skin), but I didn't want this to be one of the formatting changes you reverted, as you have sometimes done. —David Eppstein (talk) 00:02, 26 April 2013 (UTC)
- Oh, dear, the clear fixed excess whitespace I had been getting. I'll look into this more carefully, thanks.
- I wasn't offended. It was the combination of NPOV-Calc-Reform summary quickly followed by "gross formatting hack" summary that made me worry I'd pissed you off by e.g. here here, plus re frogs (about which you are absolutely, positively, unquestionably, DEAD WRONG, by the way, but we can take that up later). To know me is irresistibly to love me, but some people never get that far because I accidently piss them off right at the get-go, and I didn't want that to happen with you.
Mrs. AMG is very appreciative of our (really your) work on this. Just so you know the two new sections will grow to become more balanced, but not so fast now since DYK has come and gone. Also, I'm gonna remove the Pythag. Th. image, OK?
Gleason got 5000 clickthroughs, 3 nearest runners-up are 1/2 that or less. And Gleason beat the pants off "2013 Canadian Budget" as well as "added sugar" -- thank heaven, since it would be most disheartening to learn that the public would rather read an article on the Canadian budget than one on Andrew Gleason. I'm also going to tell Mrs. Gleason that our 5000 matches those for a hook from a few days ago re Leonard Nimoy's I Am Not Spock, which is saying something, I think (or is it no one under 50 knows who Leonard Nimoy is?). Of course being first on the list, with image, doesn't hurt.
EEng (talk) 02:48, 26 April 2013 (UTC)
- I've had IRL distractions again but wanted to drop by to acknowledge your continued good work. EEng (talk) 02:17, 10 May 2013 (UTC)
I have unreviewed a page you curated
Hi, I'm Daemonic Kangaroo. I wanted to let you know that I saw the page you reviewed, Allison Miller (disambiguation), and have un-reviewed it again. If you have any questions, please ask them on my talk page. Thank you. Daemonic Kangaroo (talk) 22:11, 29 April 2013 (UTC)
- I did not review that page; I created it. But perhaps that somehow caused it to be auto-reviewed. —David Eppstein (talk) 22:14, 29 April 2013 (UTC)
- I'm not sure what happened here. I seem to recall that I clicked on "unreview" in error and then reverted this, but didn't realise that this message had been sent automatically. Sorry to have bothered you. Best wishes. -- Daemonic Kangaroo (talk) 04:50, 30 April 2013 (UTC)
Your deletion of the Thompson entry in Godel
Dear David
You felt justified in peremptorily deleting the above without offering a justification.
I am aggrieved about this and am interested in taking it further.
I hope you have read the article. If you think its clearly makes untenable claims I suggest you respond to the following. Given the confidence your actions display a week should be enough time. its been posted elsewhere to give it the largest currency to be fair to the peremptory deleters like you.
It should be comprehensible by a computer science expert.
Godel's Theorems are not the pure stuff of mathematicians and it would not be surprising that a critique would be found in a philosophy journal. .Its a new journal. Its paywalled but you can find it (unpaywalled) at http://www.davidpublishing.com/davidpublishing/Upfile/2/29/2012/2012022981760545.pdf .
The first step is to try and read before taking down things without any acquaintance with them. A year or more ago a couple of editors tried to include something similar and it was suggested that it was too early to do so. Apart from Russell and Wittgenstein who were unhappy with the Theorems and who didn't seem to be be able to put a finger on what was wrong this is the first real challenge to the Theorems. Whilst the Theorems mights sound OK their counterpart Lob's Theorem is certainly hard to accept. As Boolos says it offerss a way of proving that Santa Claus exists. I'm not trying to give an authoritative account of what Thompson says but the paper is very short and not hard for anyone competent in logic to understand. Its certainly easier than Godel's!
A rough outline: In this context, a proof is a sequence of sentences using the standard rules of inferences and resulting in the conclusion which is also a sentence. Godel introduces the idea of arithematisation which translates a symbolic system into a system of numbers which serve an indexical function. His arithmetisation is intended to be isomorphic to the original system. He then introduces an arithmetic idea of proof which allows that any godel number of any formula is capable of proof including a single bracket. This is most odd and almost certainly wrong but doesn't matter that much.
Boolos' text talks about sentences being proved. Boolos' text does not draw a distinction between open sentences which contain a free variable and closed sentences where all the variables are bound. This doesn't seem surprising to mathematicians who tend to be focussed on formulas rather than sentences but in normal English its like using a sentence contain a pronoun where the person who is talked about is never identified. Quine, America's greatest logician point out that open sentences are true of things but not true or false in themselves. Sentences, properly so called must be true or false and open sentences are neither.
If you look at Godel's informal proof it quickly emerges that the sentence he talks about is an open sentence. As far as his formal proof is concerned arithmetic proof because it is intended to be isomorphic to ordinary proof can only be concerned with the proof of the godel numbers of closed sentences. His famous sentence starts with 'x is arithmetically unprovable' ; that formula has its own godel number; that godel number (which is the godel number of an open sentence) is then used to to create a new 'sentence' saying the godel number of the original open sentence is arithmetically unprovable. But its not a valid sentence if both proof (including arithmetic proof) is restricted to closed sentences. In theory, we could stick to Godel's idea of proof or something similar and allow open sentences into proof. But there's no good reason I can see for doing so.
If Thompson is right a lot of people will find it shocking but is that so important? I am certainly sure there is nothing crazy about what he is saying and that a lot of logicians think that there is a problem here. Lets ask all the snipping editors to get together and show (within say 7 days): Thompson's thesis rests on some untenable assumption or mode of reasoning or say Godel's approach to proof of open sentences is right. This shouldn't be too hard given their convictions about these things.
Your thoughts? Best of luck.
Fernandodelucia (talk)Fernando —Preceding undated comment added 10:15, 2 May 2013 (UTC)
- I note your deletion of the Thompson discussion. It was suggested that I put it there to allow editors to comment before I made some complaints. The aim was to offer other editors the chance to offer some reasons for saying that the Thompsson claims were untenable. As can be seen fromn the logs if there was any uncivility or discourtesy it was not from me. I will take the matter furtherFernandodelucia (talk) —Preceding undated comment added 06:44, 15 May 2013 (UTC)
Ganita Kaumudi, Narayana Pandit
I am the author of the first article which I made two weeks ago. I got a interesting reference of the third volume of Donald Knuth's The Art of Computer Programming through Google books. Will you be helpful just to give a expert look on the topic. Solomon7968 (talk) 21:03, 3 May 2013 (UTC)
Halved cube aka demihypercube graph
Hi David,
In case it interests you: fr:Graphe demi-hypercube. See also Demihypercube (géometrical approach) and Interesting Graphs and their Colourings Godsil 2004, pp 66-67. Best, --MathsPoetry (talk) 05:17, 4 May 2013 (UTC)
- Wikipédia ne possède pas d'article avec ce nom. But I found http://mathworld.wolfram.com/HalvedCubeGraph.html which is enough to convince me that this is an interesting graph that we should probably have an article about. —David Eppstein (talk) 06:00, 4 May 2013 (UTC)
- Sorry, it is fr:Demi-hypercube (graphe), I should have checked the link after typing it. And MathWorld's article was indeed my motivation for writing it, together with some remarks on fr:Graphe de Clebsch (Clebsch graph). The number of edges and vertices, the degree and the fact that they are Hamiltonian are "own work", I know it is bad, but it was so obvious... I did not include the stuff about chromatic number from Godsil, he has an upper bound for it. --MathsPoetry (talk) 08:20, 4 May 2013 (UTC)
- Ok, see new articles bipartite half and halved cube graph. —David Eppstein (talk) 20:48, 7 May 2013 (UTC)
- Oh, I missed this answer of yours.
- After reading the English version, I can make a few (unimportant) remarks:
- The mention of Hamming distance is nice, because it builds a bridge with computer science. However, I preferred using pure graph-theory language and mention one could add edges at distance 2 in .
- I preferred not giving any illustration of the complement of the Clebsch graph, because all the illustrations that we have on Commons hide one vertex behind another, or one edge behind another (as you mention it BTW).
- Why didn't you mention its hamiltonicity?
- Nice to have an article about half-bipartite graphs. Do you think it matches the geometrical notion of alternation? --MathsPoetry (talk) 19:57, 9 May 2013 (UTC)
- Ok, see new articles bipartite half and halved cube graph. —David Eppstein (talk) 20:48, 7 May 2013 (UTC)
- Sorry, it is fr:Demi-hypercube (graphe), I should have checked the link after typing it. And MathWorld's article was indeed my motivation for writing it, together with some remarks on fr:Graphe de Clebsch (Clebsch graph). The number of edges and vertices, the degree and the fact that they are Hamiltonian are "own work", I know it is bad, but it was so obvious... I did not include the stuff about chromatic number from Godsil, he has an upper bound for it. --MathsPoetry (talk) 08:20, 4 May 2013 (UTC)
Re Hamming distance: I don't see why we can't describe the same object in the languages of multiple fields, and this description is in the sources. Also I suspect that if there is a source to be found for the Hamiltonicity of this graph, it will be one that uses this formalism. Re the illustrations for n ≥ 5: Tomruen did those, and I'm not convinced that they add much to the article, but didn't want to violate WP:OWN by acting as a gatekeeper for what should be included or not. Re Hamiltonicity: it's obviously true (and should be mentioned in bipartite half — if the whole graph is Hamiltonian so is the half) but unfortunately we have no source. And re alternation: not quite. The difference is analogous to the difference between medial graphs and line graphs: when the polyhedron is not simple (it has vertices of degree four or higher) the medial graph and alternation will both remain planar, but the bipartite half and the line graph will be nonplanar (with a clique for each deleted vertex). —David Eppstein (talk) 20:06, 9 May 2013 (UTC)
- Hamming distance: it's not that we can't. It was mostly an editor choice, a matter of keeping it simple and consistant. But I should probably at least add a note on this to the French article.
- Yes, Hamiltonicity is "own work" of mine :-( . A source should not be hard to find though. And yes, it is generic to all bipartite halves.
- OK for the clique thing for deleted vertices, understood, thanks.
- The problem with the illustrations is that they might be misleading for the unattentive reader : for example, in the comp. of clebsch, they "look" like irregular graphs vith degrees like 7 or other values, while the graph itself is 10-regular. But I agree it's almost impossible to draw graphs like this one without having them look like a ball of fur. --MathsPoetry (talk) 20:27, 9 May 2013 (UTC)
- There's a prettier picture of here. I'm not sure about the order 5 case though. By the way, we should mention (we don't yet) that . That is, you can form the halved cube by adding distance-two edges to a cube of one smaller order, without taking a subset of the vertices. (Proof sketch: consider the length n − 1 binary strings together with a parity bit. If two of these strings differ by one bit, then their parity bits are different and the extended length n strings are adjacent in the halved cube. And if two of these strings differ by two bits, then their parity bits are the same and again the extended strings are adjacent in the halved cube.) —David Eppstein (talk) 20:56, 9 May 2013 (UTC)
- Oh, that's already in the French article, I thought it was on the English version as well. I even did an (ugly) drawing of a 3D cube with edges added between vertices at distance two. Feel free to reuse it if its graphical ugliness does not bother you too much.
- There's a prettier picture of here. I'm not sure about the order 5 case though. By the way, we should mention (we don't yet) that . That is, you can form the halved cube by adding distance-two edges to a cube of one smaller order, without taking a subset of the vertices. (Proof sketch: consider the length n − 1 binary strings together with a parity bit. If two of these strings differ by one bit, then their parity bits are different and the extended length n strings are adjacent in the halved cube. And if two of these strings differ by two bits, then their parity bits are the same and again the extended strings are adjacent in the halved cube.) —David Eppstein (talk) 20:56, 9 May 2013 (UTC)
- I have added right now the construction as a graph of relation between binary numbers at Hamming distance two. --MathsPoetry (talk) 21:02, 9 May 2013 (UTC)
P=NP Article
Hello Mr. Eppstein the P=NP article does not make any sense to me. Even worse none of the references or citations are neutral third parties or peer reviewed. I am told that content has to be verifiable, I was told this due to an article I was working on and I want to be a better Wikipedian by using verifiable facts. I just don't understand why the P=NP article is full of unverified content that does not need peer reviewed citations and references? Doesn't this violate the rules of Misplaced Pages? I am really confused on this, and I want to learn more about computer science and the P=NP theory. In order to do that I need more verified citations and references that are neutral third party and peer reviewed. Thomas Hard (talk) 22:42, 6 May 2013 (UTC)
- I am just a high school student but I am fascinated by the P versus NP problem. The best explanation of it I read is:
- If P = NP, then the world would be a profoundly different place than we usually assume it to be. There would be no special value in 'creative leaps,' no fundamental gap between solving a problem and recognizing the solution once it’s found. Everyone who could appreciate a symphony would be Mozart; everyone who could follow a step-by-step argument would be Gauss... — Scott Aaronson, MIT. Solomon7968 (talk) 22:59, 6 May 2013 (UTC)
I don't know what you think you mean by "neutral third parties" or "peer reviewed", but I don't think there's a big problem with the quality of the sourcing. We have sources that are both secondary (overviews of the problem) and reliably published, such as numbers 3, 4, 5, 14, 19, and 27. We have many reliably published (and generally peer reviewed) references for more specific facts that go to research papers rather than survey papers (such as numbers 1, 2, 7, 9, 10, etc) but that's ok too. And we have a few blogs and self-published lecture notes, but only by established experts in the subject (numbers 6, 8, 11, 15, etc), meeting the conditions of WP:SPS. Where there may be a problem is in the specificity of the sourcing: as you point out, there are a number of statements in the article that aren't sourced. But your strategy of peppering the article with dozens of cn tags seems counterproductive to me, and the sentences you chose seem random rather than standing out from the ones around them as being more in need of sourcing than the rest. I think it would work better either to find whole sections that are lacking references (they definitely exist here) and use one tag for the section, or place a much smaller number of cn tags more carefully, for the parts that really seem to stand out from the rest as surprising and in need of a source. And to Solomon7968, re your "best explanation", that's not saying what it *is*, it's saying what the truth of the problem *might lead to*. So it's a motivation, but not an explanation. —David Eppstein (talk) 23:14, 6 May 2013 (UTC)
- Every cited reference reads more like a Word salad than an academic paper or encyclopedia article. I put CN tags on parts of the article that were not cited. You removed them and claimed "this is very standard material — the references could definitely stand improvement" yet not improvement is made to make them better than word salad statements. Is this what Misplaced Pages has become now? Thomas Hard (talk) 16:10, 7 May 2013 (UTC)
- It is better that some articles in[REDACTED] (like computer science or Mathematics) be leaved to the experts. It is unlikely that any layman will search the web for P versus NP problem. Solomon7968 (talk) 17:02, 7 May 2013 (UTC)
- Isn't that just a cop-out to avoid making the article have better verified citations and better written to be easier to understand? You cannot just throw random stuff into an article, and when someone questions it just say 'leave it to the experts' and 'it is unlikely that any layman will search the web for it". I myself am trying to understand it, but nobody here is helping me to understand it. I don't consider myself a layman, I don't consider myself an expert on the subject either, but aren't most articles on Misplaced Pages written to help people learn and not written for experts who already understand it? I mean what is the point of Misplaced Pages if it is written so that you need a PHD on the subject to understand the article? How are people without a PHD going to understand the article and learn? Thomas Hard (talk) 19:57, 7 May 2013 (UTC)
- It is better that some articles in[REDACTED] (like computer science or Mathematics) be leaved to the experts. It is unlikely that any layman will search the web for P versus NP problem. Solomon7968 (talk) 17:02, 7 May 2013 (UTC)
- It is a computer science article. It is bound to be technical. I am not a expert but to understand the article I will suggest you to read first the Euclidean Algorithm which is the most basic algorithm and learn what is a polynomial-time algorithm. Probably then you can understand the article. Solomon7968 (talk) 20:17, 7 May 2013 (UTC)
- I checked out the page and I am really stuck with two unsourced claims:
- P versus NP problem#Context in 2nd line The most common resources are time (how many steps it takes to solve a problem) and space (how much memory it takes to solve a problem). There is a page on the time issue but no page or citation on what it means by Memory Complexity.
- P versus NP problem#Reasons to believe P ≠ NP really does not have reliable sources on the implication of the proof. There is only one reference that protein structure prediction will be affected. The rest paragraph is really full of Misplaced Pages:Peacock terms. Solomon7968 (talk) 20:54, 7 May 2013 (UTC)
- Re your first point, the article you are looking for is space complexity. I suspect it's too technical to be easily readable, though. The intuitive meaning is: how many bits of memory does your computer program use? —David Eppstein (talk) 22:41, 7 May 2013 (UTC)
- Well I know a binary 0 or 1 taks a bit space. So perhaps the number has the Space complexity of the number of bytes it takes to hold its binary representation. Am I right? or this is something else. Solomon7968 (talk) 22:47, 7 May 2013 (UTC)
- The more precise definition of space complexity is not actually in terms of bits, but rather in terms of cells of the tape of a Turing machine, and is only defined up to constant factors (blurring the distinction between bits and bytes). —David Eppstein (talk) 22:50, 7 May 2013 (UTC)
- The article Computational resource suggests you have not once edited it. I added two links, do check it and please add a link of the Cell you are talking. I could not figure out a link. Solomon7968 (talk) 22:57, 7 May 2013 (UTC)
- I don't think there is a better link than Turing machine for this. Please do remember that Misplaced Pages is an encyclopedia, not a textbook. You may be better off trying to read an actual textbook on complexity theory, of which there are many. —David Eppstein (talk) 23:05, 7 May 2013 (UTC)
Question
What was wrong with this suggestion? 94.116.38.81 (talk) 14:12, 7 May 2013 (UTC)
- Why do you think I think something was wrong with it? —David Eppstein (talk) 15:54, 7 May 2013 (UTC)
Revert of wikilink addition in Compound of three octahedra
Hi David, I noticed you undid this edit I made. I admit I am no expert. Does this mean that the redirect stellated rhombic dodecahedron is incorrect? In that case, I could start a new article for the stellated rhombic dodecahedron. Best. -- Toshio Yamaguchi 15:52, 9 May 2013 (UTC)
- Yes, the redirect is incorrect. The compound of three octahedra is different from the stellated rhombic dodecahedron. The vertex figures of the former are squares, and of the latter are rhombi. Maproom (talk) 16:20, 9 May 2013 (UTC)
- I think the redirect is there because the compound article talks about the stellation, which it resembles, but they are different shapes and should have separate articles. —David Eppstein (talk) 16:35, 9 May 2013 (UTC)
- I created a new article under First stellation of rhombic dodecahedron and pointed the redirect Escher's solid to that article. I also pointed the term stellated rhombic dodecahedron in stellated rhombic dodecahedral honeycomb to the new article. -- Toshio Yamaguchi 06:21, 10 May 2013 (UTC)
- Obviously it still needs a lot of work but thanks for starting this. —David Eppstein (talk) 06:22, 10 May 2013 (UTC)
- I created a new article under First stellation of rhombic dodecahedron and pointed the redirect Escher's solid to that article. I also pointed the term stellated rhombic dodecahedron in stellated rhombic dodecahedral honeycomb to the new article. -- Toshio Yamaguchi 06:21, 10 May 2013 (UTC)
- I think the redirect is there because the compound article talks about the stellation, which it resembles, but they are different shapes and should have separate articles. —David Eppstein (talk) 16:35, 9 May 2013 (UTC)
Courtesy notice of revert
As a courtesy, I'm letting you know I undid here http://en.wikipedia.org/search/?title=Continuous_function&diff=554524890&oldid=554059679 Transcendence
I'm not an expert with how categories work, so if this was in error with regards to the way categories work, feel free to undo my edit. (talk) 00:58, 11 May 2013 (UTC)
- Please familiarize yourself with Misplaced Pages:Categorization: "if a page belongs to a subcategory of C (or a subcategory of a subcategory of C, and so on) then it is not normally placed directly into C". Category:Mathematics should have very few articles directly in it (really, only Mathematics itself): everything else should be in a subcategory and therefore by standard Misplaced Pages categorization rules it should not also be in the parent category. —David Eppstein (talk) 01:01, 11 May 2013 (UTC)
Unblock request
You blocked IP 74.3.4.112 (talk · contribs) indefinitely in 2010 as a sock of User:Martin.musatov. The IP is now requesting unblock and says that it is a public system in an internet cafe. I am inclined to unblock and see what happens, as we don't usually indef IPs; but I'll pass the request to you as you know the background. Regards, JohnCD (talk) 19:55, 11 May 2013 (UTC)
 Done. —David Eppstein (talk) 20:07, 11 May 2013 (UTC)
Done. —David Eppstein (talk) 20:07, 11 May 2013 (UTC)
2013 Wikinic
| [REDACTED] | Great American Wikinic at Pan-Pacific Park | 
|
| You are invited to the third Great American Wikinic taking place in Pan-Pacific Park, in Los Angeles, on Saturday, June 22, 2013! We would love to see you there! —howcheng {chat} 01:03, 12 May 2013 (UTC) | ||
| If you would not like to receive future messages about meetups, please remove your name from Misplaced Pages:Meetup/LA/Invite. |
- Unlikely: that's the day I get back from RIo. —David Eppstein (talk) 02:21, 12 May 2013 (UTC)
arxiv
Hi David. Editors do not add any credibility to published material. They decide based on whether they think the material sells or not (occasionally, they might publish something for literature's sake). So if (and you seem not to be sure about it, either) the reference was printed on demand, that does not make it less reliable, only, presumably, less of a good business. 88.27.6.12 (talk) 09:43, 15 May 2013 (UTC)
- That may be true for your opinion of the credibility of the mateiral, but it is not how Misplaced Pages's policy on reliable sources works. —David Eppstein (talk) 15:12, 15 May 2013 (UTC)
Vladimir Ronin
I have posted a response to your entry on the AfD, which you may care to consider. Kind regards Jono2013 (talk) 11:09, 15 May 2013 (UTC)
Talkback

Message added 19:28, 15 May 2013 (UTC). You can remove this notice at any time by removing the {{Talkback}} or {{Tb}} template.
Codename Lisa (talk) 19:28, 15 May 2013 (UTC)
incompleteness
Hi David, part of the thread at incompleteness theorem that you moved to /Arguments deals with the issue of whether Kunen's formulation of the incompleteness theorem should be included in the page. Recall that currently only "true but unprobableunprovable" formulations currently appear in the page. Kunen's formulation (sourced in the thread) is of type "cannot be proved or disproved". Thus, the thread deals with an issue related to improving the page. Tkuvho (talk) 12:54, 16 May 2013 (UTC)
- Uh, oh! Please let's not add the "true but unprobable" into the mix -- last thing we need is a lot of Bayesians and catastrophe theorists joining this circus as well. EEng (talk) 13:49, 16 May 2013 (UTC)
- I don't think Kenneth Kunen associates with those types :-) Tkuvho (talk) 15:21, 16 May 2013 (UTC)
precise definition of vortex in graph minor structure theorem
Hi David -- in the precise definition of vortices, it says: "A circular interval for F is a set of vertices of the form {v_a, v_{a+1}, ..., v_{a+s}} where a and k are integers and where subscripts are reduced modulo n." k is later used to define the depth of the vortex. In this sentence, though, should the s be a k or vice versa? I was going to fix it myself, but then I realized that I wasn't sure. Thanks! — Preceding unsigned comment added by Glencora (talk • contribs) 23:06, 16 May 2013 (UTC)
- Hi Cora. I think the "where a and k are integers" should be "a and s" — the later k means something different. I've gone ahead and made that change. —David Eppstein (talk) 23:27, 16 May 2013 (UTC)
Grammatical evolution
This page has got virtually no edits since 2006 though a Google scholar search lists 1 close to 400 hits. Please take a expert look on the article. Solomon7968 (talk) 16:25, 17 May 2013 (UTC)
- I'm not very interested in general heuristic search techniques that don't guarantee runtime or result approximation quality, sorry. —David Eppstein (talk) 19:10, 17 May 2013 (UTC)
OOPs, probably you misunderstood what I said. As this article was largely written by a single User:Whenning I thought to cross check whether this is notable or not. Or in other words if this is suitable for wikipedia. I have zero knowledge of the topic. Solomon7968 (talk) 19:50, 17 May 2013 (UTC)
- Oh, I think something with that many GS hits is almost certainly notable enough. —David Eppstein (talk) 20:35, 17 May 2013 (UTC)
Invitation to take a short survey about communication and efficiency of WikiProjects for my research
Hi David, I'm working on a project to study the running of WikiProject and possible performance measures for it. I learn from WikiProject Mathematics talk page that you are an active member of the project. I would like to invite you to take a short survey for my study. If you are available to take our survey, could you please reply an email to me? I'm new to Misplaced Pages, I can't send too many emails to other editors due to anti-spam measure. Thank you very much for your time. Xiangju (talk) 15:37, 22 May 2013 (UTC)
The Grassmanns Justus, Hermann and Robert
Hi David,
I am suggesting that you add a link or a note referring to the work and influence of the Grassmanns in he section in which you discuss Riemann's Contribution.
I have written extensively on the Grassmanns in my blogs which you will find if you google "jehovajah Grassmann".
It is not appropriate to do more than a brief entry in this page , but it is less appropriate to leave them out! — Preceding unsigned comment added by Jehovajah (talk • contribs) 00:00, 27 May 2013 (UTC)
- Which article are you talking about? —David Eppstein (talk) 00:02, 27 May 2013 (UTC)
This section in Geometry.
″===Geometry beyond Euclid===
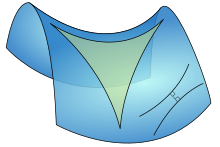
For nearly two thousand years since Euclid, while the range of geometrical questions asked and answered inevitably expanded, basic understanding of space remained essentially the same. Immanuel Kant argued that there is only one, absolute, geometry, which is known to be true a priori by an inner faculty of mind: Euclidean geometry was synthetic a priori. This dominant view was overturned by the revolutionary discovery of non-Euclidean geometry in the works of Gauss (who never published his theory), Bolyai, and Lobachevsky, who demonstrated that ordinary Euclidean space is only one possibility for development of geometry. A broad vision of the subject of geometry was then expressed by Riemann in his 1867 inauguration lecture Über die Hypothesen, welche der Geometrie zu Grunde liegen (On the hypotheses on which geometry is based), published only after his death. Riemann's new idea of space proved crucial in Einstein's general relativity theory and Riemannian geometry, which considers very general spaces in which the notion of length is defined, is a mainstay of modern geometry.″
If yoou did not write it or contribute to it , i am sorry. However could you direct me to who did in that case?Jehovajah (talk) 00:17, 27 May 2013 (UTC)
- It wasn't me, but it doesn't matter who wrote it; see WP:OWN. What matters is the consensus of the editors who remain interested in this article. So probably you would be best off taking this to Talk:Geometry where they could see it and discuss it. —David Eppstein (talk) 04:22, 27 May 2013 (UTC)
Thanks DavidJehovajah (talk) 08:53, 27 May 2013 (UTC)
Proposed deletion of Steven Lehar article
Hi: Someone has removed the PROD saying they "believe that this article represents an important nexus between Gestalt theory and neurophysiology." and that they "will elaborate" but are trying to "beat the time limit." I am pretty ignorant of how the PROD process goes here, so I may have a few questions about next steps if the editor's attempt doesn't fare well. I suppose I (or we?) will just have to cross the bridge if we get to it, and I just wanted to keep you in the loop in case you aren't watching the page. Thanks! Rschwieb (talk) 13:33, 28 May 2013 (UTC)
- Thanks. The obvious next step is to take it to an AfD. —David Eppstein (talk) 15:54, 28 May 2013 (UTC)
- PS on looking at this again (and particularly looking at his citation record in Google Scholar) I think there is a case to be made for passing WP:PROF, so although it has been so very badly sourced for eight years now (making a mockery of the "time limit" comment) it may be better to clean it up than to delete it. —David Eppstein (talk) 06:25, 1 June 2013 (UTC)
- Well, thanks for the advice. The whole thing that drew my attention to it was this, which I think when you read both the poster's question and self-answer, you will see why I doubted the value of the article. What happens if nobody cleans it up? I certainly don't think I could... Rschwieb (talk) 16:40, 1 June 2013 (UTC)
- PS on looking at this again (and particularly looking at his citation record in Google Scholar) I think there is a case to be made for passing WP:PROF, so although it has been so very badly sourced for eight years now (making a mockery of the "time limit" comment) it may be better to clean it up than to delete it. —David Eppstein (talk) 06:25, 1 June 2013 (UTC)
About image in Tesseract article
Hello Mr. Eppstein! I noticed you reverted my edit which added apparently a 'yet another image' to Tesseract article which was already rich in images. Actually this isn't the case. None of the image were traditional 2D representation of a tesseract. By traditional I mean what you do to make a cube on blackboard. All of them were Schlegel. So thinking need of at least one pure 2D representation I added it. Rawal of Jaisalmer (talk) 17:05, 1 June 2013 (UTC)
- They all appear two-dimensional on my screen. All of them. They are made of two-dimensional pixels. What about yours is special in that respect? —David Eppstein (talk) 17:11, 1 June 2013 (UTC)
- As I said they are using Schlegel which is not same as Isometric projection, ie what I do. They are diagrams of different families. Schlegel diagrams use isometrically 3D components to show 4D and are in now way 4D analog of 3D cube made by pure isometric projection. In other ways, Schlegel is in two steps, 1st step is making isometric projection of a 3D scenario and with respect to that tries to show a 4D scenario. This is a two step process. When you draw a cube in 2D you can directly do isometric projection and in one step it is done. But this wasn't done on 4D because of reasons like confusion of position of A'and B', same for H' and E'. This problem in my diagram is first time solved by use of colors and notations. So indeed this diagram is different to rest there. If some useless diagram have to be removed then I think there are already too may Schlegel diagrams to remove, removing only direct projection of 4D in 2D plane would be counter productive. It shows another (arguably easier?) view point in understanding what 4D space really is. So I again say diagram should be there, if you think there are too many diagrams remove any Schlegel diagrams. Rawal of Jaisalmer (talk) 03:38, 2 June 2013 (UTC)
- File:4-cube t0.svg, which was already in the article, is an isometric projection, and much prettier than yours. More, I'm not convinced that yours is actually isometric. Shouldn't it be true that, in an isometric embedding, each group of edges that are parallel to each other in 4d remain parallel and the same length? But in your drawing they aren't all the same length. —David Eppstein (talk) 03:50, 2 June 2013 (UTC)
- It is essentially of same length but appears otherwise. Most importance are given to angles. Diagram you cited is again not true isometric, I would disagree. That is again 2 step process. You can't just remove things without proper reason. Tell me the Misplaced Pages policy dealing with it. Rawal of Jaisalmer (talk) 05:30, 2 June 2013 (UTC)
- Meh, I like Rawal of Jaisalmer's more. --OCCullens (talk) 05:32, 2 June 2013 (UTC)
- The policy is, hash it out on Talk:Tesseract and try to obtain a consensus of the editors interested in that article. My personal opinion is that there are already far too many images there, so one more, especially of questionable meaning, is a step in the wrong direction. Ok, you say the angles are important, but they're wrong too: there are lots of 45 degree angles in your drawing, none in the actual tesseract. What part of the geometry, exactly, do you think it does depict accurately? What principle was used to obtain that drawing? What should a viewer be expected to learn about the tesseract by viewing that drawing that he or she would not learn from the other drawings? —David Eppstein (talk) 06:56, 2 June 2013 (UTC)
- Meh, I like Rawal of Jaisalmer's more. --OCCullens (talk) 05:32, 2 June 2013 (UTC)
- It is essentially of same length but appears otherwise. Most importance are given to angles. Diagram you cited is again not true isometric, I would disagree. That is again 2 step process. You can't just remove things without proper reason. Tell me the Misplaced Pages policy dealing with it. Rawal of Jaisalmer (talk) 05:30, 2 June 2013 (UTC)
- File:4-cube t0.svg, which was already in the article, is an isometric projection, and much prettier than yours. More, I'm not convinced that yours is actually isometric. Shouldn't it be true that, in an isometric embedding, each group of edges that are parallel to each other in 4d remain parallel and the same length? But in your drawing they aren't all the same length. —David Eppstein (talk) 03:50, 2 June 2013 (UTC)
- As I said they are using Schlegel which is not same as Isometric projection, ie what I do. They are diagrams of different families. Schlegel diagrams use isometrically 3D components to show 4D and are in now way 4D analog of 3D cube made by pure isometric projection. In other ways, Schlegel is in two steps, 1st step is making isometric projection of a 3D scenario and with respect to that tries to show a 4D scenario. This is a two step process. When you draw a cube in 2D you can directly do isometric projection and in one step it is done. But this wasn't done on 4D because of reasons like confusion of position of A'and B', same for H' and E'. This problem in my diagram is first time solved by use of colors and notations. So indeed this diagram is different to rest there. If some useless diagram have to be removed then I think there are already too may Schlegel diagrams to remove, removing only direct projection of 4D in 2D plane would be counter productive. It shows another (arguably easier?) view point in understanding what 4D space really is. So I again say diagram should be there, if you think there are too many diagrams remove any Schlegel diagrams. Rawal of Jaisalmer (talk) 03:38, 2 June 2013 (UTC)
45 degree respect to what? Angles are not absolute but relative... They(cube's angles)are absolutely 90 in respect to cube. Angle of the line segments joining edges of cube ABCDEFGH to there Tesseractic counterparts and length of those lines are also subjective to position of ABCDEFGH in tesseract. Angles and lenght would only be equal if it is absolutely in center of tesseract. I have measured length of cube ABCDEFGH's sides properly all are 100 points (by illustrator). Even if you see this diagram- http://upload.wikimedia.org/wikipedia/commons/a/a2/Schlegel_wireframe_8-cell.png There length don't appear to be same but are intended. Now question of what it can explain. A person who is new into these field of study, coming from classical maths/physics use normal isometric projection, label edges by (A, B, C... A', B'...), etc. Schlegel is absolutely not something they know about. It is for those casual knowledge seekrs who just want to know what tesseract really is without getting into details like special schlegel diagrams for it. If there work can be done in 2 minutes by my diagram why to make them first study about Schlegel diagrams? And then try to find what tesseract is? Rawal of Jaisalmer (talk) 12:07, 2 June 2013 (UTC)
- So may I consider consensus is reached and I may add image again? Rawal of Jaisalmer (talk) 08:40, 4 June 2013 (UTC)
Hello! There is a DR/N request you may have interest in.

This message is being sent to let you know of a discussion at the Misplaced Pages:Dispute resolution noticeboard regarding a content dispute discussion you may have participated in. Content disputes can hold up article development and make editing difficult for editors. You are not required to participate, but you are both invited and encouraged to help find a resolution. Please join us to help form a consensus. Thank you! -- Nbound (talk) 09:17, 4 June 2013 (UTC)
Edit War
You seem to be rude and unhelpful. You fail to discuss with no reply in many days. Then on what basis on EARTH you are reverting edits when you don't show enough courage to even discuss? That is extremely rude and offensive. I would report this to admins... Rawal of Jaisalmer (talk) 04:07, 6 June 2013 (UTC)
- Please see WP:BRD. This is normal editing progression. You make a bold change (your new image). Other editors object and revert. Then we talk on the talk page on the article and reach a consensus before you make any more attempts to restore the change. So far, I don't see you as having convinced anyone else that your change is an improvement. As for your bizarre complaint that I have not discussed this: see two sections up on this talk page, and (as soon as I made my most recent revert) this contribution to the article talk page. —David Eppstein (talk) 04:22, 6 June 2013 (UTC)
Stochastic cellular automaton
Hi, Re Stochastic cellular automaton,
<<can you please explain what you mean by your edit summary "copyright problems should be solved"? As far as I can tell (1) the original article was entirely copied inappropriately from other sources,>> when I tried to create a "probabilistic cellular automata" page, I noticed a "stochastic cellular automata" already exists. No sense to have a double page, just add a link to the existing page. No idea if it was copyrighted. I just added parts I wrote, no copyrighted.
<<(2) the article you moved back to Stochastic cellular automaton is identical to the version that was proposed for deletion because of these copyright problems. What exactly do you think has been done to "solve" the copyright problem here?>> the sections declared as problematic were cancelled. I can cancel more up to what I remember I did myself.
<<the comment above by GiantSnowman about consulting an administrator before moving back into article space: which administrator have you consulted? My first reaction is to move the article back into user space (or delete it) until I see some evidence that the copyright problems are indeed solved, but I'll wait for a day or so first to give you a chance to respond.>>
Absolutely no idea how I should contact an administrator and was thinking the "move" imply the agreement of an administrator, which is the case : you answered. PierreYvesLouis (talk) 21:36, 8 June 2013 (UTC)PierreYvesLouis
- The article as it exists now (even after your recent deletion) still contains material copied from research papers. It should not have been moved into article space until all such text was completely removed. —David Eppstein (talk) 21:45, 8 June 2013 (UTC)
Graph for abc
Is this a good idea, or not? --bender235 (talk) 15:08, 9 June 2013 (UTC)
Squaring the Circle
Dear Mr. Eppstein,
I realize that it is not possible to accomplish this task by traditional methods and I know why. Nevertheless, why did you delete my entry on the Misplaced Pages article about squaring the circle? Surely, the figures represented on my website are constructed with compass & straightedge. And if you consider them to be embedded in smooth Riemannian manifolds of positive curvature (i.e., perfect spheres) proportional to those depicted in my diagrams, they do indeed encompass a total amount of surface area exactly equal to pi. This finding is significant and indisputable. These shapes even retain most of their Euclidean characteristics despite the change in manifold. The square, for example, in both cases is embedded in a two-dimensional manifold, all four sides are equal in length, all angles are congruent; intersecting at right angles, the diagonal still obeys the Pythagorean Theorem, and for all intents & purposes opposite sides are "parallel." In other words, if you draw lines of longitude (i.e., great circles) through both sides of the "square," they will intersect each side orthogonally, and all points on one side remain equidistant from their corresponding points on the opposite side throughout their respective lengths.
Please respond at your earliest convenience.
Kindest regards, C. RicciRicci4.4428828 (talk) 00:46, 10 June 2013 (UTC)
- For the short answer to your question "Why?": See WP:NOR and WP:ELNO #11. —David Eppstein (talk) 01:01, 10 June 2013 (UTC)
Dear Mr. Eppstein,
Thank you for responding so quickly. I understand these reasons. I know you are a busy man & I've already taken much of your valuable time. If only I could ask one more thing: Will you please take another look at the website & let me know what you (personally) think? I know you are a highly educated & well respected man, and I would greatly appreciate any feedback I might gain. I worked very hard & long on this despite the fact that I already knew the feat was considered "impossible." The solution I arrived at is very unique & I'm sure there are many who would find it most intriguing; that is, if I could find an appropriate place to post it. Any suggestions or comments you might have will be seriously considered & greatly appreciated.
Again, thank you for your time.
C. RicciRicci4.4428828 (talk) 01:43, 10 June 2013 (UTC)
- I haven't looked at your web site but it is obvious that in a uniformly positively or negatively curved space there exist radii for which the circle of that radius has rational area, or has equal area to a square with rational side lengths (whichever you prefer), simply because this ratio varies continuously as a function of radius rather than being fixed at an irrational constant. —David Eppstein (talk) 02:11, 10 June 2013 (UTC)
User repeatedly adding an unwanted image at Tessellation
Hallo, I just went to User talk:Aughost to notify that user of a discussion I've started on the Tessellation talk page: an image that didn't seem to me necessary appeared in the article today; I reverted it with a brief explanation in the edit comment, and the user at once put it back. I wouldn't have taken it further, except that I saw your warning notice on the same issue (from January this year) just above, so perhaps you might like to keep an eye on the situation. All the best - Chiswick Chap (talk) 11:46, 19 June 2013 (UTC)
M. T. Naraniengar
Hello, Since you have access to JSTOR and HighBeam can you please help in the article. I have added a JSTOR reference which contains his biography. Thanks in advance. The Legend of Zorro 21:23, 19 June 2013 (UTC)
- I added a little from the JSTOR obit but there's nothing more there than the first page, which appears to be public. I think my highbeam access has expired. —David Eppstein (talk) 02:27, 20 June 2013 (UTC)
- Is "The Mathematics Student" published by Indian Mathematical Society available in Jstor or Highbeam? The page 200 to 201 in this contains his biography. The Legend of Zorro 08:22, 20 June 2013 (UTC)
Wondering why you un-PROD-ded Hayford Peirce
This is an article about a science fiction writer where there are essentially no independent third-party reviews of his books. My guess is mostly these books are self-published. There was a listing of the author in a science-fiction encyclopedia. I did some serious google searching and did not find anything remotely indicating reliable sources. So, my question: why did you un-PROD the Hayford Peirce page?--Tomwsulcer (talk) 11:46, 23 June 2013 (UTC)
- Tor is one of the biggest mainstream SF publishers, and Betancourt and Wildside are also known SF publishers. These are not self-published books. —David Eppstein (talk) 16:05, 23 June 2013 (UTC)
- Let's suppose they were not self-published. Where are reliable third-party reviews? Where is commentary on this author or these books? A mere listing of an author in an SF encyclopedia seems barely enough. My question remains: why did you support inclusion of this article?--Tomwsulcer (talk) 18:34, 23 June 2013 (UTC)
- Let's suppose you are not an idiot and can determine the difference between self-publishing and a reputable publisher yourself. Then, you should take that information to the AfD. —David Eppstein (talk) 20:24, 23 June 2013 (UTC)
- Let's suppose they were not self-published. Where are reliable third-party reviews? Where is commentary on this author or these books? A mere listing of an author in an SF encyclopedia seems barely enough. My question remains: why did you support inclusion of this article?--Tomwsulcer (talk) 18:34, 23 June 2013 (UTC)
- Kline (1972) "Mathematical thought from ancient to modern times", Oxford University Press, p. 1032. Kant did not reject the logical (analytic a priori) possibility of non-Euclidean geometry, see Jeremy Gray, "Ideas of Space Euclidean, Non-Euclidean, and Relativistic", Oxford, 1989; p. 85. Some have implied that, in light of this, Kant had in fact predicted the development of non-Euclidean geometry, cf. Leonard Nelson, "Philosophy and Axiomatics," Socratic Method and Critical Philosophy, Dover, 1965; p.164.
- http://www.maths.tcd.ie/pub/HistMath/People/Riemann/Geom/
 such that a graph
such that a graph  can be embedded in the n-dimensional Euclidean space
can be embedded in the n-dimensional Euclidean space  with every edge of
with every edge of  .
.
 . That is, you can form the halved cube by adding distance-two edges to a cube of one smaller order, without taking a subset of the vertices. (Proof sketch: consider the length n − 1 binary strings together with a parity bit. If two of these strings differ by one bit, then their parity bits are different and the extended length n strings are adjacent in the halved cube. And if two of these strings differ by two bits, then their parity bits are the same and again the extended strings are adjacent in the halved cube.) —
. That is, you can form the halved cube by adding distance-two edges to a cube of one smaller order, without taking a subset of the vertices. (Proof sketch: consider the length n − 1 binary strings together with a parity bit. If two of these strings differ by one bit, then their parity bits are different and the extended length n strings are adjacent in the halved cube. And if two of these strings differ by two bits, then their parity bits are the same and again the extended strings are adjacent in the halved cube.) —