This is an old revision of this page, as edited by Dixtosa talk | contribs ) at 12:55, 30 June 2013 (XD). The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision .
Revision as of 12:55, 30 June 2013 by Dixtosa talk | contribs ) (XD)(diff ) ← Previous revision | Latest revision (diff ) | Newer revision → (diff )
This...
This user has been on Misplaced Pages for 19 years, 8 months and 1 day .
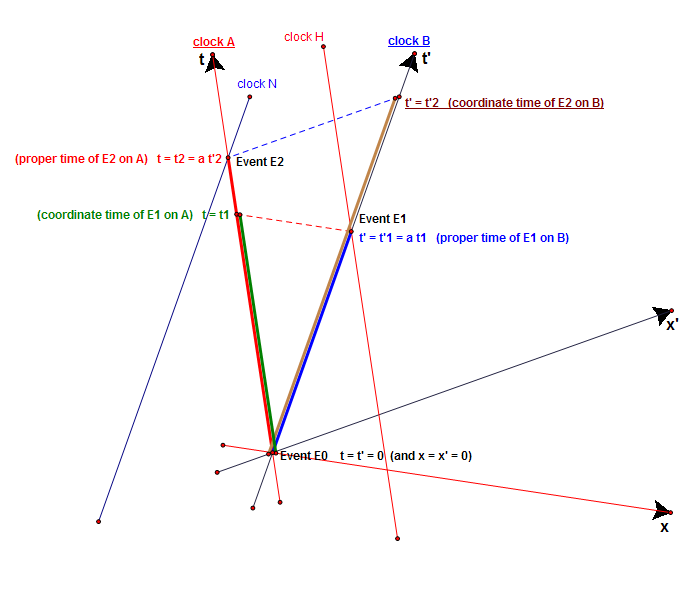
A trivial refutation of one of Dingle's Fumbles (Ref: Talk:Herbert Dingle Archive )
On page 230 in this appendix to "Science At the Crossroads" , Dingle writes:
(start quote) Thus, between events E0 and E1, A advances by
t
1
{\displaystyle \color {ForestGreen}{t_{1}}}
t
1
′
=
a
t
1
{\displaystyle \color {Blue}{t'_{1}=at_{1}}}
rate of A
rate of B
=
t
1
a
t
1
=
1
a
>
1
(3)
{\displaystyle {\frac {\color {ForestGreen}{\text{rate of A}}}{\color {Blue}{\text{rate of B}}}}={\frac {\color {ForestGreen}{t_{1}}}{\color {Blue}{at_{1}}}}={\frac {1}{a}}>1\qquad {\text{(3)}}}
...
Thus, between events E0 and E2, B advances by
t
2
′
{\displaystyle \color {Brown}{t'_{2}}}
t
2
=
a
t
2
′
{\displaystyle \color {Red}{t_{2}=at'_{2}}}
rate of A
rate of B
=
a
t
2
′
t
2
′
=
a
<
1
(4)
{\displaystyle {\frac {\color {Red}{\text{rate of A}}}{\color {Brown}{\text{rate of B}}}}={\frac {\color {Red}{at'_{2}}}{\color {Brown}{t'_{2}}}}=a<1\qquad {\text{(4)}}}
Equations (3) and (4) are contradictory: hence the theory requiring them must be false. (end quote) Dingle should have written as follows:
(start correction) Thus, between events E0 and E1, A, which is not present at both events, advances by
t
1
{\displaystyle \color {ForestGreen}{t_{1}}}
present at both events, by
t
1
′
=
a
t
1
{\displaystyle \color {Blue}{t'_{1}=at_{1}}}
rate of clock not present at both events E0 and E1
rate of clock present at both events E0 and E1
=
coordinate time of E1
proper time of E1
=
rate of A
rate of B
=
t
1
t
1
′
=
t
1
a
t
1
=
1
a
>
1
(3)
{\displaystyle {\frac {\color {ForestGreen}{\text{rate of clock not present at both events E0 and E1}}}{\color {Blue}{\text{rate of clock present at both events E0 and E1}}}}={\frac {\color {ForestGreen}{\text{coordinate time of E1}}}{\color {Blue}{\text{proper time of E1}}}}={\frac {\color {ForestGreen}{\text{rate of A}}}{\color {Blue}{\text{rate of B}}}}={\frac {\color {ForestGreen}{t_{1}}}{\color {Blue}{t'_{1}}}}={\frac {\color {ForestGreen}{t_{1}}}{\color {Blue}{at_{1}}}}={\frac {1}{a}}>1\qquad {\text{(3)}}}
...
Thus, between events E0 and E2, B, which is not present at both events, advances by
t
2
′
{\displaystyle \color {Brown}{t'_{2}}}
present at both events, by
t
2
=
a
t
2
′
{\displaystyle \color {Red}{t_{2}=at'_{2}}}
rate of clock not present at both events E0 and E2
rate of clock present at both events E0 and E2
=
coordinate time of E2
proper time of E2
=
rate of B
rate of A
=
t
2
′
t
2
=
t
2
′
a
t
2
′
=
1
a
>
1
(4)
{\displaystyle {\frac {\color {Brown}{\text{rate of clock not present at both events E0 and E2}}}{\color {Red}{\text{rate of clock present at both events E0 and E2}}}}={\frac {\color {Brown}{\text{coordinate time of E2}}}{\color {Red}{\text{proper time of E2}}}}={\frac {\color {Brown}{\text{rate of B}}}{\color {Red}{\text{rate of A}}}}={\frac {\color {Brown}{t'_{2}}}{\color {Red}{t_{2}}}}={\frac {\color {Brown}{t'_{2}}}{\color {Red}{at'_{2}}}}={\frac {1}{a}}>1\qquad {\text{(4)}}}
Equations (3) and (4) are consistent and say that any event's coordinate time is always larger than its proper time: hence there is no reason to say that the theory requiring them must be false.
(end correction) DVdm 12:18, 6 August 2007 (UTC)
Text is available under the Creative Commons Attribution-ShareAlike License. Additional terms may apply.
**DISCLAIMER** We are not affiliated with Wikipedia, and Cloudflare.
The information presented on this site is for general informational purposes only and does not constitute medical advice.
You should always have a personal consultation with a healthcare professional before making changes to your diet, medication, or exercise routine.
AI helps with the correspondence in our chat.
We participate in an affiliate program. If you buy something through a link, we may earn a commission 💕
↑
 and B by
and B by  by (1). Therefore
by (1). Therefore

 and A by
and A by  by (2). Therefore
by (2). Therefore


