This is an old revision of this page, as edited by David Eppstein (talk | contribs) at 21:05, 30 May 2016 (Undid revision 722904147 by R.e.b. (talk) teach the controversy — there are two valid but different defs of Archimedean and we should't take sides over which one is the right one). The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.
Revision as of 21:05, 30 May 2016 by David Eppstein (talk | contribs) (Undid revision 722904147 by R.e.b. (talk) teach the controversy — there are two valid but different defs of Archimedean and we should't take sides over which one is the right one)(diff) ← Previous revision | Latest revision (diff) | Newer revision → (diff)| Elongated square gyrobicupola | |
|---|---|
 | |
| Type | Johnson J36 - J37 - J38 |
| Faces | 8 triangles 18 squares |
| Edges | 48 |
| Vertices | 24 |
| Vertex configuration | 8+16(3.4) |
| Symmetry group | D4d |
| Dual polyhedron | Pseudo-deltoidal icositetrahedron |
| Properties | convex, singular vertex figure |
| Net | |
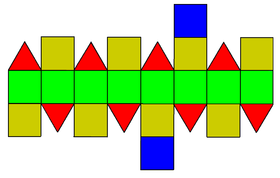 | |
In geometry, the elongated square gyrobicupola or pseudorhombicuboctahedron is one of the Johnson solids (J37). It is sometimes considered to be an Archimedean solid, because its faces consist of regular polygons that meet in the same pattern at each of its vertices. However, unlike the rest of the Archimedean solids, it lacks a set of global symmetries that take every vertex to every other vertex.
This shape may have been discovered by Johannes Kepler in his enumeration of the Archimedean solids, but its first clear appearance in print appears to be the work of Duncan Sommerville in 1905. It was independently rediscovered by J. C. P. Miller in 1930 (allegedly by mistake while attempting to construct a model of the rhombicuboctahedron) and again by V. G. Ashkinuse in 1957.
A Johnson solid is one of 92 strictly convex polyhedra that is composed of regular polygon faces but are not uniform polyhedra (that is, they are not Platonic solids, Archimedean solids, prisms, or antiprisms). They were named by Norman Johnson, who first listed these polyhedra in 1966.
Construction and relation to the rhombicuboctahedron
As the name suggests, it can be constructed by elongating a square gyrobicupola (J29) and inserting an octagonal prism between its two halves.
 Rhombicuboctahedron |
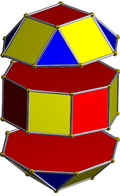 Exploded sections of rhombicuboctahedron |
 Pseudo-rhombicuboctahedron |
The solid can also be seen as the result of twisting one of the square cupolae (J4) on a rhombicuboctahedron (one of the Archimedean solids; a.k.a. the elongated square orthobicupola) by 45 degrees. It is therefore a gyrate rhombicuboctahedron. Its similarity to the rhombicuboctahedron gives it the alternative name pseudorhombicuboctahedron. It has occasionally been referred to as "the fourteenth Archimedean solid".
This property does not carry over to its pentagonal-faced counterpart, the gyrate rhombicosidodecahedron.
Symmetry and classification
The elongated square gyrobicupola possesses D4d symmetry. It is locally vertex-regular — the arrangement of the four faces incident on any vertex is the same for all vertices; this is unique among the Johnson solids. However, it is not vertex-transitive, and consequently not usually considered to be one of the Archimedean solids, as there are pairs of vertices such that there is no isometry of the solid which maps one into the other. Essentially, the two types of vertices can be distinguished by their "neighbors of neighbors." Another way to see that the polyhedron is not vertex-transitive is to note that there is exactly one belt of eight squares around its equator, which distinguishes vertices on the belt from vertices on either side. With faces colored by its D4d symmetry, it can look like this:
| pseudorhombicuboctahedron | Pseudo-deltoidal icositetrahedron (Dual) | |
|---|---|---|
 net |
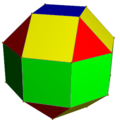
|

|
There are 8 (green) squares around its equator, 4 (red) triangles and 4 (yellow) squares above and below, and one (blue) square on each pole.
Related polyhedra and honeycombs
The elongated square gyrobicupola can form a space-filling honeycomb with the regular tetrahedron, cube, and cuboctahedron. It can also form another honeycomb with the tetrahedron, square pyramid and various combinations of cubes, elongated square pyramids, and elongated square bipyramids.
References
- Sommerville, D. M. Y. (1905), "Semi-regular networks of the plane in absolute geometry", Transactions of the Royal Society of Edinburgh, 41: 725–747, doi:10.1017/s0080456800035560. As cited by Grünbaum (2009).
- Grünbaum, Branko (2009), "An enduring error" (PDF), Elemente der Mathematik, 64 (3): 89–101, doi:10.4171/EM/120, MR 2520469 Reprinted in Pitici, Mircea, ed. (2011). The Best Writing on Mathematics 2010. Princeton University Press. pp. 18–31..
- Johnson, Norman W. (1966), "Convex polyhedra with regular faces", Canadian Journal of Mathematics, 18: 169–200, doi:10.4153/cjm-1966-021-8, MR 0185507, Zbl 0132.14603.
- "J37 honeycombs", Gallery of Wooden Polyhedra, retrieved 2016-03-21
Additional reading
- Anthony Pugh (1976), Polyhedra: A visual approach, California: University of California Press Berkeley, ISBN 0-520-03056-7 Chapter 2: Archimedean polyhedra, prisma and antiprisms, p. 25 Pseudo-rhombicuboctahedron
External links
- Weisstein, Eric W., "Elongated square gyrobicupola" ("Johnson solid") at MathWorld.
- George Hart: pseudo-rhombicuboctahedra