Misplaced Pages

This is an old revision of this page, as edited by WillowW (talk | contribs) at 21:51, 15 September 2006 (it's important to define "light" for the rest of the article). The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.

Photon
Classification
Elementary particle Boson Gauge boson Electromagnetic interaction
Properties
Symbol: ${\displaystyle \gamma \ \mathrm {or} \ h\nu }$ Mass: 0 Electric Charge: 0 Spin: 1

In modern physics, the photon is the elementary particle responsible for electromagnetic interactions. It is the fundamental constituent of light, i.e., all forms of electromagnetic radiation.

The modern concept of the photon was developed gradually (1905-1917) by Albert Einstein to account for experimental observations that cannot be explained by the classical wave model of light. In particular, the photon model captured the dependence of light's energy and momentum on its frequency, and accounted for the ability of matter and radiation to be in thermal equilibrium. Other physicists sought to explain these anomalous observations by semiclassical models, in which light is still described by Maxwell's equations but the material objects that emit and absorb light are quantized. Although these semiclassical models contributed to the development of quantum mechanics, experiments eventually proved Einstein's hypothesis that light itself is particulate.

The photon concept led to many advances in theoretical and experimental physics, such as the laser, Bose–Einstein condensation, quantum field theory, and the probabilistic interpretation of quantum mechanics. According to the best modern theory of physics (the so-called Standard Model), photons are responsible for producing all electric and magnetic fields, and are themselves the product of requiring that physical laws have a certain symmetry at every point in spacetime. The intrinsic properties of photons (such as charge, mass and spin) are determined by the properties of this gauge symmetry. Photons have many applications in technology, such as super-powerful quantum computers and unbreakable quantum cryptography.

Nomenclature

The photon was originally called a "light quantum" (das Lichtquant) by its inventor, Albert Einstein. The modern name "photon" derives from the Greek word Template:Polytonic, "phōs" (meaning light) and was coined in 1926 by the distinguished physical chemist Gilbert N. Lewis, who published a speculative theory in which photons were "uncreatable and indestructible". Although Lewis' theory was never accepted — being contradicted by many experiments — his new name, photon, was adopted immediately by most physicists.

In physics, a photon is usually denoted by the symbol ${\displaystyle \gamma \!}$, the Greek letter gamma. In chemistry and optical engineering, photons are usually symbolized by ${\displaystyle h\nu \!}$ (the energy of a photon) where ${\displaystyle h\!}$ is Planck's constant and ${\displaystyle \nu \!}$ (the Greek letter nu) is the photon's frequency.

Physical properties of the photon

The photon is massless, has no electric charge and does not decay spontaneously in empty space. A photon has two possible helicities (polarization states) and is described by three continuous parameters: the components of its wave vector, which determine its wavelength ${\displaystyle \lambda \!}$ and its direction of propagation. Photons are emitted in many natural processes, e.g., when a charge is accelerated, when an atom or a nucleus jumps from a higher to lower energy level, or when a particle and its antiparticle are annihilated. Photons are absorbed in the time-reversed processes, e.g., in the production of particle–antiparticle pairs or in an atomic or nuclear transition to a higher energy level.

Since the photon is massless, the photon moves at ${\displaystyle c\!}$ (the speed of light in empty space) and its energy ${\displaystyle E\!}$ and momentum ${\displaystyle \mathbf {p} }$ are related by ${\displaystyle E=c\,p\!}$, where ${\displaystyle p\!}$ is the magnitude of the momentum. For comparison, the corresponding equation for particles with an invariant mass ${\displaystyle m\!}$ would be ${\displaystyle E^{2}=c^{2}p^{2}+m^{2}c^{4}\!}$, as shown in special relativity.

The energy and momentum of a photon depend only on its frequency ${\displaystyle \nu \!}$ or, equivalently, its wavelength ${\displaystyle \lambda \!}$

${\displaystyle E=\hbar \omega =h\nu \!}$

${\displaystyle \mathbf {p} =\hbar \mathbf {k} }$

and consequently the magnitude of the momentum is

${\displaystyle p=\hbar k={\frac {h}{\lambda }}={\frac {h\nu }{c}}}$

where ${\displaystyle \hbar }$ is Planck's reduced constant, ${\displaystyle h/2\pi \!}$; ${\displaystyle \mathbf {k} }$ is the wave vector and ${\displaystyle k\!}$ is its magnitude, the wave number, ${\displaystyle 2\pi /\lambda \!}$; and ${\displaystyle \omega \!}$ is the angular frequency, ${\displaystyle 2\pi \nu \!}$. Notice that ${\displaystyle \mathbf {k} }$ points in the direction of the photon's propagation. The photon also carries spin angular momentum that does not depend on its frequency; the component of the spin in the direction of the momentum is ${\displaystyle \pm \hbar }$.

To illustrate these formulae, the annihilation of a particle with its antiparticle must result in at least two photons (not one) for the following reason. In the center of mass frame, the colliding antiparticles have no net momentum, whereas a single photon always has momentum. Hence, conservation of momentum requires that at least two photons are created, with zero net momentum. The energy of the two photons (and, hence, their frequency) may be determined from conservation of four-momentum. The reverse process, pair production, is the dominant mechanism by which high-energy photons (such as gamma rays) lose energy while passing through matter.

The classical formulae for the energy and momentum of electromagnetic radiation can be re-expressed in terms of photon events. For example, the pressure of electromagnetic radiation on an object derives from the transfer of photon momentum per unit time and unit area to that object, since pressure is force per unit area and force is the change in momentum per unit time.

Historical development of the photon concept

Most theories up to the eighteenth century hypothesized that light was composed of particles. Since particle models cannot easily account for the refraction, diffraction and birefringence of light, wave theories of light were proposed by René Descartes (1637), Robert Hooke (~1665), and Christian Huygens (1678); however, particle models remained the dominant theory, chiefly due to the influence of Isaac Newton. In the early nineteenth century, Thomas Young and August Fresnel clearly demonstrated the interference and diffraction of light and, by 1850, wave models had become dominant. In 1865, James Clerk Maxwell's prediction that light was an electromagnetic wave — which was confirmed experimentally in 1888 by Heinrich Hertz's detection of radio waves — seemed to be the final blow to particle models of light.

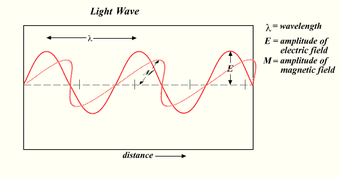
The Maxwell wave theory, however, does not account for all properties of light. The Maxwell theory predicts that the energy of a light wave depends only on its intensity, not on its frequency; nevertheless, several independent types of experiments show that the energy imparted by light to atoms depends only on the light's frequency, not on its intensity. For example, some chemical reactions can be provoked only by light of frequency higher than a certain threshold; light of lower frequency, no matter how intense, is incapable of exciting the reaction. Similarly, electrons can be ejected from a metal plate by shining light of sufficiently high frequency on it (the photoelectric effect); the energy of the ejected electron is related only to the light's frequency, not to its intensity.

At the same time, investigations of blackbody radiation carried out over four decades (1860–1900) by various researchers culminated in Max Planck's hypothesis that the energy of any system that absorbs or emits electromagnetic radiation of frequency ${\displaystyle \nu \!}$ is an integer multiple of an energy quantum ${\displaystyle E=h\nu \!}$. As shown by Albert Einstein, some form of energy quantization must be assumed to account for the thermal equilibrium observed between matter and electromagnetic radiation.

Since the Maxwell theory of light allows for all possible energies of electromagnetic radiation, most physicists assumed initially that the energy quantization resulted from some unknown constraint on the matter that absorbs or emits the radiation. In 1905, Einstein was the first to propose that energy quantization was a property of electromagnetic radiation itself. Although he accepted the validity of Maxwell's theory, Einstein pointed out that many anomalous experiments could be explained if the energy of a Maxwellian light wave were localized into point-like quanta that move independently of one another, even if the wave itself is spread continuously over space. In 1909 and 1916, Einstein showed that, if Planck's law of black-body radiation is accepted, the energy quanta must also carry momentum ${\displaystyle p={\frac {h}{\lambda }}}$, making them full-fledged particles. This photon momentum was observed experimentally by Arthur Compton, for which he received the Nobel Prize in 1927. The pivotal question was then: how to unify Maxwell's wave theory of light with its experimentally observed particle nature? The answer to this question occupied Albert Einstein for the rest of his life, and was solved in quantum electrodynamics and its successor, the Standard Model.

Early objections to the photon hypothesis

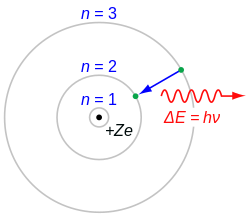
Einstein's 1905 predictions were verified experimentally in several ways within the first two decades of the 20th century, as recounted in Robert Millikan's Nobel lecture. However, before Compton's famous experiment in 1922, most physicists were reluctant to believe that electromagnetic radiation itself might be particulate. (See, for example, the Nobel lectures of Wien, Planck and Millikan.) This reluctance is understandable, given the success and plausibility of Maxwell's electromagnetic wave model of light. Therefore, most physicists assumed rather that energy quantization resulted from some unknown constraint on the matter that absorbs or emits radiation. Niels Bohr, Arnold Sommerfeld and others developed atomic models with discrete energy levels that could account qualitatively for the sharp spectral lines and energy quantization observed in the emission and absorption of light by atoms; their models agreed excellently with the spectrum of hydrogen, but not with those of other atoms. It was only the Compton scattering of a photon by a free electron (which can have no energy levels, since it has no internal structure) that convinced most physicists that light itself was quantized.

Even after Compton's experiment, Bohr, Hendrik Kramers and John Slater made one last attempt to preserve the Maxwell's continuous electromagnetic field model of light, the so-called BKS model. To account for the then-available data, two drastic hypotheses had to be made:

• Energy and momentum are conserved only on the average in interactions between matter and radiation, not in elementary processes such as absorption and emission. This allows one to reconcile the discontinuously changing energy of the atom (jump between energy states) with the continuously release of energy into radiation.

• Causality is abandoned. For example, spontaneous emissions are merely emissions induced by a "virtual" electromagnetic field.

However, refined Compton experiments showed that energy-momentum is conserved extraordinarily well in elementary processes; and also that the jolting of the electron and the generation of a new photon in Compton scattering obey causality to within 10 ps. Accordingly, Bohr and his co-workers gave their model "as honorable a funeral as possible". Nevertheless, the BKS model inspired Werner Heisenberg in his development of quantum mechanics.

A few physicists persisted in developing semiclassical models in which electromagnetic radiation is not quantized, but matter obeys the laws of quantum mechanics. Although the evidence for photons from chemical and physical experiments was overwhelming by the 1970's, this evidence could not be considered as absolutely definitive; since it relied on the interaction of light with matter, a sufficiently complicated theory of matter could in principle account for the evidence. Nevertheless, all semiclassical theories were refuted definitively in the 1970's and 1980's by elegant photon-correlation experiments. Hence, Einstein's hypothesis that quantization is a property of electromagnetic radiation itself is considered to be proven.

Wave–particle duality

The dual wave–particle nature of photons is difficult to visualize, and warrants further discussion. On the one hand, the photon displays diffraction and interference (wave phenomena) on the length scale of its wavelength. For example, a single photon passing through a double-slit experiment lands on the screen with a probability distribution given by its interference pattern determined by Maxwell's equations. However, experiments confirm that the photon is not a short pulse of electromagnetic radiation; it does not spread out as it propagates, nor does it divide when it encounters a beam splitter. Rather, the photon seems like a point-like particle, since it is absorbed or emitted as a whole by arbitrarily small systems, systems much smaller than its wavelength, such as an atomic nucleus (≈10 m across) or even the point-like electron. Nevertheless, the photon is not a point-like particle whose trajectory is shaped probabilistically by the electromagnetic field, as conceived by Einstein and others; that hypothesis was also refuted by the photon-correlation experiments cited above. According to our present understanding, the electromagnetic field itself is produced by photons, which in turn result from a local gauge symmetry and the laws of quantum field theory (see below).

The quantum mechanics of material particles features an uncertainty principle that forbids the simultaneous measurement of the position and momentum of a particle in the same direction. An analogous principle for photons forbids the simultaneous measurement of the number ${\displaystyle n}$ of photons (see Fock state and below) in an electromagnetic wave and the phase ${\displaystyle \phi }$ of that wave

${\displaystyle \Delta n\Delta \phi >1}$

See coherent state and squeezed coherent state for more details.

Remarkably, the quantization of light into photons and even the frequency dependence of the photon's energy and momentum can be seen as necessary consequences of the quantum mechanics of charged, material particles such as the electron. An elegant illustration is Werner Heisenberg's thought experiment for locating an electron with an ideal microscope. The position of the electron can be determined to within the resolving power of the microscope, which is given by a formula from classical optics

${\displaystyle \Delta x\sim {\frac {\lambda }{\sin \theta }}}$

where ${\displaystyle \theta }$ is the aperture angle of the microscope. Thus, the position uncertainty ${\displaystyle \Delta x}$ can be made arbitrarily small by reducing the wavelength (e.g., gamma rays). The momentum of the electron is uncertain, since it received a "kick" ${\displaystyle \Delta p}$ from the light scattering from it into the microscope. If light were not quantized into photons, the uncertainty ${\displaystyle \Delta p}$ could be made arbitrarily small by reducing the light's intensity. In that case, since the wavelength and intensity of light can be varied independently, one could simultaneously determine the position and momentum to arbitrarily high accuracy, violating the uncertainty principle. By contrast, Einstein's photon momentum law preserves the uncertainty principle; since the photon is scattered anywhere within the aperture, the uncertainty of momentum transferred equals

${\displaystyle \Delta p\sim p_{\mathrm {photon} }\sin \theta ={\frac {h}{\lambda }}\sin \theta }$

giving the product ${\displaystyle \Delta x\Delta p\,\sim \,h}$, which is Heisenberg's uncertainty principle. Thus, all the world is quantized; both matter and fields must obey a consistent set of quantum laws, if either one is to be quantized (more below).

Bose–Einstein model of a photon gas

In 1924, Satyendra Nath Bose derived Planck's law of black-body radiation without using any electromagnetism, but rather a modification of coarse-grained counting of phase space. Einstein showed that this modification is equivalent to assuming that photons are rigorously identical and that it implied a "mysterious non-local interaction", now understood as the requirement for a symmetric quantum mechanical state. This work led to the concept of coherent states and the development of the laser. In the same papers, Einstein extended Bose's formalism to material particles (bosons) and predicted that they would condense into their lowest quantum state at low enough temperatures (Bose–Einstein condensation).

Photons must obey Bose–Einstein statistics if they are to allow the superposition principle of electromagnetic fields (i.e., the condition that Maxwell's equations are linear). All particles are divided into bosons and fermions, depending on whether they have integer or half-integer spin, respectively. The spin-statistics theorem shows that all bosons obey Bose–Einstein statistics, whereas all fermions obey Fermi-Dirac statistics or, equivalently, the Pauli exclusion principle, which states that at most one particle can occupy any given state. Thus, if the photon were a fermion, only one photon could move in a particular direction at a time. This is inconsistent with the experimental observation that lasers can produce coherent light of arbitrary intensity, that is, with many photons moving in the same direction. Hence, the photon must be a boson and obey Bose–Einstein statistics. As described below, photons have spin 1, corresponding to their two possible helicities (corresponding to left- and right-circularly polarized light).

Stimulated and spontaneous emission

In 1916, Einstein showed that Planck's quantum hypothesis ${\displaystyle E=h\nu }$ could be derived from a kinetic rate equation. Consider a cavity in thermal equilibrium and filled with electromagnetic radiation and systems that can emit and absorb that radiation. Thermal equilibrium requires that the number density ${\displaystyle \rho (\nu )}$ of photons with frequency ${\displaystyle \nu }$ is constant in time; hence, the rate of emitting photons of that frequency must equal the rate of absorbing them.

Einstein hypothesized that the rate ${\displaystyle R_{ji}}$ for a system to absorb a photon of frequency ${\displaystyle \nu }$ and transition from a lower energy ${\displaystyle E_{j}}$ to a higher energy ${\displaystyle E_{i}}$ was proportional to the number ${\displaystyle N_{j}}$ of molecules with energy ${\displaystyle E_{j}}$ and to the number density ${\displaystyle \rho (\nu )}$ of ambient photons with that frequency

${\displaystyle R_{ji}=N_{j}B_{ji}\rho (\nu )\!}$

where ${\displaystyle B_{ji}}$ is the rate constant for absorption.

More daringly, Einstein hypothesized that the reverse rate ${\displaystyle R_{ij}}$ for a system to emit a photon of frequency ${\displaystyle \nu }$ and transition from a higher energy ${\displaystyle E_{i}}$ to a lower energy ${\displaystyle E_{j}}$ was composed of two terms:

${\displaystyle R_{ij}=N_{i}A_{ij}+N_{i}B_{ij}\rho (\nu )\!}$

where ${\displaystyle A_{ij}}$ is the rate constant for emitting a photon spontaneously, and ${\displaystyle B_{ij}}$ is the rate constant for emitting it in response to ambient photons (induced or stimulated emission). Einstein showed that Planck's energy law ${\displaystyle E=h\nu }$ is a necessary consequence of these hypothesized rate equations and the basic requirements that the ambient radiation be in thermal equilibrium with the systems that absorb and emit the radiation and independent of the systems' material composition.

This simple kinetic model was a powerful stimulus for research. Einstein was able to show that ${\displaystyle B_{ij}=B_{ji}}$ (i.e., the rate constants for induced emission and absorption are equal) and, perhaps more remarkably,

${\displaystyle A_{ij}={\frac {8\pi h\nu ^{3}}{c^{3}}}B_{ij}}$

Einstein did not attempt to justify his rate equations but noted that ${\displaystyle A_{ij}}$ and ${\displaystyle B_{ij}}$ should be derivable from a "mechanics and electrodynamics modified to accommodate the quantum hypothesis". This prediction was borne out in quantum mechanics and quantum electrodynamics, respectively; both are required to derive Einstein's rate constants from first principles. Paul Dirac derived the ${\displaystyle B_{ij}}$ rate constants in 1926 using a semiclassical approach, and, in 1927, succeeded in deriving all the rate constants from first principles. Dirac's work was the foundation of quantum electrodynamics, i.e., the quantization of the electromagnetic field itself. Dirac's approach is also called second quantization or quantum field theory; the earlier quantum mechanics (the quantization of material particles moving in a potential) represents the "first quantization".

Einstein was troubled by the fact that his theory seemed incomplete, since it did not determine the direction of a spontaneously emitted photon. A probabilistic nature of light-particle motion was first considered by Newton in his treatment of birefringence and, more generally, of the splitting of light beams at interfaces into a transmitted beam and a reflected beam. Newton hypothesized that hidden variables in the light particle determined which path it would follow. Similarly, Einstein hoped for a more complete theory that would leave nothing to chance, beginning his separation from quantum mechanics. Ironically, Max Born's probabilistic interpretation of the wave function was inspired by Einstein's later work searching for a more complete theory.

Second quantization

In 1910, Peter Debye derived Planck's law of black-body radiation from a relatively simple assumption. He correctly decomposed the electromagnetic field in a cavity into its Fourier modes, and assumed that the energy in any mode was an integer multiple of ${\displaystyle h\nu \!}$, where ${\displaystyle \nu \!}$ is the frequency of the electromagnetic mode. Planck's law of black-body radiation follows immediately as a geometric sum. However, Debye's approach failed to give the correct formula for the energy fluctuations of blackbody radiation, which were derived by Einstein in 1909.

In 1925, Born, Heisenberg and Jordan reinterpreted Debye's concept in a key way. The electromagnetic Fourier modes (defined by their wave vector ${\displaystyle \mathbf {k} }$ and polarization state) are equivalent to a set of uncoupled simple harmonic oscillators, as may be shown classically. Treated quantum mechanically, the energy levels of such oscillators are known to be ${\displaystyle E=nh\nu \!}$, where ${\displaystyle \nu \!}$ is the oscillator frequency. The key new step was to identify an electromagnetic mode with energy ${\displaystyle E=nh\nu \!}$ as a state with ${\displaystyle n\!}$ photons, each of energy ${\displaystyle h\nu \!}$. This approach gives the correct energy fluctuation formula.

Dirac took this one step further. He treated the interaction between a charge and an electromagnetic field as a small perturbation that induces transitions in the photon states, changing the numbers of photons in the modes, while conserving energy and momentum overall. Dirac was able to derive Einstein's ${\displaystyle A_{ij}\!}$ and ${\displaystyle B_{ij}\!}$ coefficients from first principles, and showed that the Bose–Einstein statistics of photons is a natural consequence of quantizing the electromagnetic field correctly. (Bose's reasoning went in the opposite direction; he derived Planck's law of black body radiation by assuming BE statistics.) In Dirac's time, it was not yet known that all bosons, including photons, must obey BE statistics.

Dirac's second-order perturbation theory can involve virtual photons, transient intermediate states of the electromagnetic field; the static electric and magnetic interactions are mediated by such virtual photons. In such quantum field theories, the probability of observable events is calculated by summing over all possible intermediate steps, even ones that are unphysical; hence, virtual photons are not constrained to satisfy ${\displaystyle E=p\,c\!}$, and may have extra polarization states (three or four depending on the gauge used, instead of the two states of real photons). Although these transient virtual photons can never be observed, they contribute measurably to the probabilities of observable events. Indeed, such second-order and higher-order perturbation calculations can make infinite contributions, a problem that was overcome in quantum electrodynamics by using renormalization.

In modern physics notation, the quantum state of the electromagnetic field is written as a Fock state, a tensor product of the states for each electromagnetic mode

${\displaystyle |n_{k_{0}}\rangle \otimes |n_{k_{1}}\rangle \otimes \dots \otimes |n_{k_{n}}\rangle \dots }$

where ${\displaystyle |n_{k_{i}}\rangle }$ represents the state in which ${\displaystyle \,n_{k_{i}}}$ photons are in the mode ${\displaystyle \,k_{i}}$. In this notation, the creation of a new photon in mode ${\displaystyle \,k_{i}}$ (e.g., emitted from an atomic transition) is written as ${\displaystyle |n_{k_{i}}\rangle \rightarrow |n_{k_{i}}+1\rangle }$. This notation merely expresses the concept of Born, Heisenberg and Jordan described above, and does not add any physics.

The photon as a gauge boson

The electromagnetic field can be understood as a gauge theory, i.e., as a field that results from requiring that a symmetry hold independently at every position in spacetime. For the electromagnetic field, this gauge symmetry is the U(1) symmetry of a complex number, i.e., the ability to vary the phase of a complex number without affecting real numbers constructed from it (such as the energy or the Lagrangian).

The quanta of a gauge field must be massless bosons, as long as the symmetry is not broken; hence, the photon is predicted to be massless and to have integer spin. The particular form of the electromagnetic interaction specifies that the photon must have zero electric charge and spin ±1, i.e, its spin (not orbital) angular momentum measured along its direction of motion must be ${\displaystyle \pm \hbar }$. These two components correspond to the classical concepts of right-handed and left-handed circularly polarized light. However, the transient virtual photons of quantum electrodynamics may also adopt unphysical polarization states.

In the prevailing Standard Model of physics, the photon is one of four gauge bosons in the electroweak interaction; the other three are denoted W, W and Z and are responsible for the weak interaction. Unlike the photon, these gauge bosons have invariant mass, owing to a mechanism that breaks their SU(2) gauge symmetry. The unification of the photon with W and Z gauge bosons in the electroweak interaction was accomplished by Sheldon Glashow, Abdus Salam and Steven Weinberg, for which they were awarded the 1979 Nobel Prize in physics. Physicists continue to hypothesize grand unified theories that connect these four gauge bosons with the eight gluon gauge bosons of quantum chromodynamics; however, key predictions of these theories (such as proton decay) have not been observed experimentally.

Contributions of photons to the invariant mass of a system

Although the photon is itself massless, it adds to the invariant mass of any system to which it belongs; this is true for every form of energy, as predicted by the special theory of relativity. For example, the invariant mass of a system that emits a photon is decreased by an amount ${\displaystyle {E}/{c^{2}}}$ upon emission (where ${\displaystyle E}$ is the energy of the photon in the frame of the emitting system). Similarly, the invariant mass of a system that absorbs a photon is increased by a corresponding amount based on the energy of the photon in the frame of the absorbing system.

This concept is applied in a key prediction of QED, the theory of quantum electrodynamics begun by Dirac (described above). QED is able to predict the magnetic dipole moment of leptons (such as that of the electron) to extremely high accuracy (16 decimal places); experimental measurements of these magnetic dipole moments have agreed with these predictions perfectly. The predictions, however, require counting the contributions of virtual photons to the invariant mass of the lepton. Another example of such contributions verified experimentally is the QED prediction of the hyperfine structure (the Lamb shift) of bound lepton pairs, such as muonium and positronium.

Since photons contribute to the stress-energy tensor, they exert a gravitational attraction on other objects, according to the theory of general relativity. Conversely, photons are themselves affected by gravity; their normally straight trajectories may be bent by warped spacetime (cf. gravitational lensing) and their frequencies may be lowered by moving to a higher gravitational potential (cf. the Pound-Rebka experiment). However, these effects are not specific to photons; exactly the same effects would be predicted for classical electromagnetic waves.

Photons in matter

Photons of different frequencies travel through matter at different speeds; this is called dispersion. In matter, the photon blends with quantum excitations of the matter (quasi-particles such as phonons and excitons) to form a polariton; this polariton has a nonzero effective mass, which means that it cannot travel at c, the speed of light in a vacuum. This is the formal reason why light is slower in media (such as glass) than in vacuum. The polariton propagation speed ${\displaystyle v}$ (its group velocity) is the derivative of the energy with respect to momentum

${\displaystyle v={\frac {d\omega }{dk}}={\frac {dE}{dp}}}$

where, as above, ${\displaystyle E}$ and ${\displaystyle p}$ are the photon's energy and momentum magnitude, and ${\displaystyle \omega }$ and ${\displaystyle k}$ are its angular frequency and wave number, respectively. In some cases, the dispersion can result in extremely slow speeds of light. The effects of photon interactions with other quasi-particles may be observed directly in Raman scattering and Brillouin scattering.

Recent research in photons

The fundamental nature of the photon is believed to be understood theoretically; the prevailing Standard Model predicts that the photon is a massless, chargeless boson of spin 1 that results from a local U(1) gauge symmetry and mediates the electromagnetic interaction. However, physicists continue to check for discrepancies between experiment and the Standard Model predictions, in the hopes of finding clues to physics beyond the Standard Model. In particular, physicists continue to set ever better upper limits on the charge and mass of the photon; a nonzero value for either parameter would be a serious violation of the Standard Model. However, all experimental data hitherto are consistent with the photon having zero charge and mass. The best universally accepted upper limits on the photon charge and mass are 10 C and 1.8x10 kg, respectively.

Much research has been devoted to applications of photons in the field of quantum optics. Photons seem well-suited to be elements of an ultra-fast quantum computer, and the quantum entanglement of photons is a focus of research. Nonlinear optical processes (such as two-photon absorption, self-phase modulation and optical parametric oscillators) are another active research area, although such processes generally do not require the assumption of photons per se; they may often be modeled by treating atoms as nonlinear oscillators. The nonlinear process of spontaneous parametric down conversion is often used to produce single-photon states. Finally, photons are essential in some aspects of optical communication, especially for quantum cryptography.

See also

• Light
• Electromagnetic radiation
• Quantum optics
• Photonics
• Photon polarization

Footnotes

1. ^ Einstein, A (1905). "Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt (trans. A Heuristic Model of the Creation and Transformation of Light)". Annalen der Physik. 17: 132–148. Template:De icon. An English translation is available from Wikisource.
2. ^ Einstein, A (1909). "Über die Entwicklung unserer Anschauungen über das Wesen und die Konstitution der Strahlung (trans. The Development of Our Views on the Composition and Essence of Radiation)". Physikalische Zeitschrift. 10: 817–825. Template:De icon. An English translation is available from Wikisource.
3. ^ Einstein, A (1916a). "Strahlungs-emission und -absorption nach der Quantentheorie". Verhandlungen der Deutschen Physikalischen Gesellschaft. 18: 318. Template:De icon
4. ^ Einstein, A (1916b). "Zur Quantentheorie der Strahlung". Mitteilungen der Physikalischen Geselschaft zu Zürich. 16: 47. Also Physikalische Zeitschrift, 18, 121—128 (1917). Template:De icon
5. Lewis, GN (1926). "The conservation of photons". Nature. 118: 874–875.
6. The intrinsic or "invariant" mass of the photon is believed to be exactly zero, based on experiment and theoretical considerations, as described above. This is the standard definition of "mass" among physicists. However, some popularizations of physics have ascribed to the photon a relativistic mass, defined as E/c, where E represents the photon's energy. See mass in special relativity for a discussion of the relationship between invariant mass and relativistic mass.
7. ^ Cocconi, G (1992). "Upper Limits on the Electric Charge of the Photon". American Journal of Physics. 60: 750–751. {{cite journal}}: External link in |title= (help)
8. ^ Newton, I (1730). Opticks (4th edition ed.). Dover Publications. pp. Book II, Part III, Propositions XII-XX, Queries 25-29. ISBN 0-486-60205-2. {{cite book}}: |edition= has extra text (help)
9. Buchwald, Jed Z. (1989). The Rise of the Wave Theory of Light: Optical Theory and Experiment in the Early Nineteenth Century. University of Chicago Press. ISBN 0226078868.
10. Maxwell, JC (1865). "A Dynamical Theory of the Electromagnetic Field". Philosophical Transactions of the Royal Society of London. 155: 459–512. This article followed a presentation by Maxwell on 8 December 1864 to the Royal Society.
11. Hertz, H (1888). "Über Strahlen elektrischer Kraft". Sitzungsberichte der Preussischen Akademie der Wissenschaften (Berlin). 1888: 1297–1307.
12. ^ "Wilhelm Wien Nobel Lecture". Delivered 11 December 1911.
13. Planck, M (1901). "Über das Gesetz der Energieverteilung im Normalspectrum". Annalen der Physik. 4: 553–563. Template:De icon
14. ^ "Max Planck's Nobel Lecture". Delivered 2 June 1920.
15. ^ Compton, A (1923). "A Quantum Theory of the Scattering of X-rays by Light Elements". Physical Review. 21: 483–502.
16. ^ "Robert A. Millikan's Nobel Lecture". Delivered 23 May 1924.
17. Bohr, N (1924). "The Quantum Theory of Radiation". Philosophical Magazine. 47: 785–802. {{cite journal}}: Unknown parameter |coauthors= ignored (|author= suggested) (help) Also Zeitschrift für Physik, 24, 69 (1924).
18. ^ Pais, A (1982). Subtle is the Lord: The Science and the Life of Albert Einstein. Oxford University Press. pp. 364–388, 402–415.
19. Heisenberg Nobel lecture, delivered 11 December 1933.
20. Mandel, L (1976). E. Wolf, ed. (ed.). "The case for and against semiclassical radiation theory". Progress in Optics. XIII. North-Holland: 27–69. {{cite journal}}: |editor= has generic name (help)
21. ^ These experiments produce results that cannot be explained by any classical theory of light, since they involve anticorrelations that result from the quantum measurement process. In 1974, the first such experiment was carried out by Clauser, who reported a violation of a classical Cauchy–Schwarz inequality. In 1977, Kimble et al. demonstrated a analogous anti-bunching effect of photons interacting with a beam splitter; this approach was simplified and sources of error eliminated in the photon-anticorrelation experiment of Grangier et al. (1986). This work is reviewed and simplified further in Thorn et al. (2004). (These references are listed below under Additional references.)
22. Taylor, GI (1909). "Interference fringes with feeble light". Proceedings of the Cambridge Philosophical Society. 15: 114–115.
23. Heisenberg, W (1927). "Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik". Zeitschrift für Physik. 43: 172–198.
24. Bose, SN (1924). "Plancks Gesetz und Lichtquantenhypothese". Zeitschrift für Physik. 26: 178–181. Template:De icon
25. Einstein, A (1924). "Quantentheorie des einatomigen idealen Gases". Sitzungsberichte der Preussischen Akademie der Wissenschaften (Berlin), Physikalisch-mathematische Klasse. 1924: 261–267. Template:De icon
26. Einstein, A (1925). "Quantentheorie des einatomigen idealen Gases, Zweite Abhandlung". Sitzungsberichte der Preussischen Akademie der Wissenschaften (Berlin), Physikalisch-mathematische Klasse. 1925: 3–14. Template:De icon
27. Dirac, PAM (1926). "On the Theory of Quantum Mechanics". Proc. Roy. Soc. A. 112: 661–677.
28. ^ Dirac, PAM (1927a). "The Quantum Theory of the Emission and Absorption of Radiation". Proc. Roy. Soc. A. 114: 243–265.
29. ^ Dirac, PAM (1927b). "The Quantum Theory of Dispersion". Proc. Roy. Soc. A. 114: 710–728.
30. Heisenberg, W (1929). "Zur Quantentheorie der Wellenfelder". Zeitschrift für Physik. 56: 1. {{cite journal}}: Unknown parameter |coauthors= ignored (|author= suggested) (help) Template:De icon
31. Heisenberg, W (1930). "Zur Quantentheorie der Wellenfelder". Zeitschrift für Physik. 59: 139. {{cite journal}}: Unknown parameter |coauthors= ignored (|author= suggested) (help) Template:De icon
32. Fermi, E (1932). "Quantum Theory of Radiation". Reviews of Modern Physics. 4: 87.
33. Born, M (1926a). "Zur Quantenmechanik der Stossvorgänge". Zeitschrift für Physik. 37: 863–867. Template:De icon
34. Born, M (1926b). "Zur Quantenmechanik der Stossvorgänge". Zeitschrift für Physik. 38: 803. {{cite journal}}: Cite has empty unknown parameter: |1= (help) Template:De icon
35. Pais, A (1986). Inward Bound: Of Matter and Forces in the Physical World. Oxford University Press. Specifically, Born claimed to have been inspired by Einstein's never-published attempts to develop a "ghost-field" theory, in which point-like photons are guided probabilistically by ghost fields that follow Maxwell's equations.
36. Debye, P (1910). "Der Wahrscheinlichkeitsbegriff in der Theorie der Strahlung". Annalen der Physik. 33: 1427–1434. Template:De icon
37. Born, M (1925). "Quantenmechanik II". Zeitschrift für Physik. 35: 557–615. {{cite journal}}: Unknown parameter |coauthors= ignored (|author= suggested) (help) Template:De icon
38. ^ Ryder, LH (1996). Quantum field theory (2nd edition ed.). Cambridge University Press. ISBN 0521478146. {{cite book}}: |edition= has extra text (help)
39. Sheldon Glashow Nobel lecture, delivered 8 December 1979.
40. Abdus Salam Nobel lecture, delivered 8 December 1979.
41. Steven Weinberg Nobel lecture, delivered 8 December 1979.
42. (a) Goldhaber, AS (1971). "Terrestrial and Extraterrestrial Limits on The Photon Mass". Reviews of Modern Physics. 43: 277—296. {{cite journal}}: External link in |title= (help)
    (b) Fischbach, E (1994). "New Geomagnetic Limits on the Photon Mass and on Long-Range Forces Coexisting with Electromagnetism". Physical Review Letters. 73: 514—517. {{cite journal}}: Unknown parameter |coauthors= ignored (|author= suggested) (help)
    (c) Official particle table http://pdg.lbl.gov/2005/tables/gxxx.pdf
    (d) Davis, L (1975). "Limit on Photon Mass Deduced from Pioneer-10 Observations of Jupiter's Magnetic Field". Physical Review Letters. 35: 1402—1405. {{cite journal}}: Unknown parameter |coauthors= ignored (|author= suggested) (help)
    (e) Luo, J (1999). "Determination of the limit of photon mass and cosmic magnetic vector with rotating torsion balance". Physical Review A. 270: 288—292. {{cite journal}}: Unknown parameter |coauthors= ignored (|author= suggested) (help)
    (f) Schaeffer, BE (1999). "Severe limits on variations of the speed of light with frequency". Physical Review Letters. 82: 4964—4966.
    (g) Luo, J (2003). "New experimental limit on the photon rest mass with a rotating torsion balance". Physical Review Letters. 90: Art. No. 081801. {{cite journal}}: Unknown parameter |coauthors= ignored (|author= suggested) (help)
    (h) Williams, ER (1971). "New Experimental Test of Coulomb's Law: A Laboratory Upper Limit on the Photon Rest Mass". Physical Review Letters. 26: 721–724. {{cite journal}}: External link in |title= (help); Unknown parameter |coauthors= ignored (|author= suggested) (help)
    (i) Lakes, R (1998). "Experimental Limits on the Photon Mass and Cosmic Magnetic Vector Potential". Physical Review Letters. 80: 1826. {{cite journal}}: External link in |title= (help)
    (j) 2006 PDG listing for photon
    (k) Adelberger E, Dvali G, and Gruzinov A, Photon Mass Bound Destroyed by Vortices, preprint

Additional references

• Clauser, JF. (1974). "Experimental distinction between the quantum and classical field-theoretic predictions for the photoelectric effect". Phys. Rev. D. 9: 853–860.

• Kimble, HJ (1977). "Photon Anti-bunching in Resonance Fluorescence". Phys. Rev. Lett. 39: 691. {{cite journal}}: Unknown parameter |coauthors= ignored (|author= suggested) (help)

• Grangier, P (1986). "Experimental Evidence for a Photon Anticorrelation Effect on a Beam Splitter: A New Light on Single-Photon Interferences". Europhysics Letters. 1: 501–504. {{cite journal}}: Unknown parameter |coauthors= ignored (|author= suggested) (help)

• Thorn, JJ (2004). "Observing the quantum behavior of light in an undergraduate laboratory". American Journal of Physics. 72: 1210–1219. {{cite journal}}: Unknown parameter |coauthors= ignored (|author= suggested) (help)

• Pais, A. (1982). Subtle is the Lord: The Science and the Life of Albert Einstein. Oxford University Press. pp. 364–388, 402–415. An excellent history of the photon's early development.

• "Ray Glauber's Nobel Lecture, "100 Years of Light Quanta"". Delivered 8 December 2005. Another history of the photon, summarized by a key physicist who developed the concepts of coherent states of photons.

External links

• The Nature of Light: What Is A Photon? OPN Trends, Oct 2003
• MISN-0-212 Characteristics of Photons (PDF file) by Peter Signell and Ken Gilbert for Project PHYSNET.
• How to entangle photons experimentally

Template:Elementary

• Bosons
• Electromagnetism
• Optics