This is the current revision of this page, as edited by Halibutt (talk | contribs) at 00:18, 27 October 2017 (←Created page with '=== Lorentz transformations === {{main|Lorentz transformation|Lorentz group}} #Summary Lorentz transformations|'''''Click here for a brief section summary'''''...'). The present address (URL) is a permanent link to this version.
Revision as of 00:18, 27 October 2017 by Halibutt (talk | contribs) (←Created page with '=== Lorentz transformations === {{main|Lorentz transformation|Lorentz group}} #Summary Lorentz transformations|'''''Click here for a brief section summary'''''...')(diff) ← Previous revision | Latest revision (diff) | Newer revision → (diff)Lorentz transformations
Main articles: Lorentz transformation and Lorentz groupClick here for a brief section summary
The Galilean transformations and their consequent commonsense law of addition of velocities work well in our ordinary low-speed world of planes, cars and balls. Beginning in the mid-1800s, however, sensitive scientific instrumentation began finding anomalies that did not fit well with the ordinary addition of velocities.
To transform the coordinates of an event from one frame to another in special relativity, we use the Lorentz transformations.
The Lorentz factor appears in the Lorentz transformations:
The inverse Lorentz transformations are:
When v ≪ c, the v/c and vx/c terms approach zero, and the Lorentz transformations approximate to the Galilean transformations.
As noted before, when we write and so forth, we most often really mean and so forth. Although, for brevity, we write the Lorentz transformation equations without deltas, it should be understood that x means Δx, etc. We are, in general, always concerned with the space and time differences between events.
Note on nomenclature: Calling one set of transformations the normal Lorentz transformations and the other the inverse transformations is misleading, since there is no intrinsic difference between the frames. Different authors call one or the other set of transformations the "inverse" set. The forwards and inverse transformations are trivially related to each other, since the S frame can only be moving forwards or reverse with respect to S′. So inverting the equations simply entails switching the primed and unprimed variables and replacing v with −v.
Example: Terence and Stella are at an Earth-to-Mars space race. Terence is an official at the starting line, while Stella is a participant. At time t = t′ = 0, Stella's spaceship accelerates instantaneously to a speed of 0.5 c. The distance from Earth to Mars is 300 light-seconds (about 90.0×10 km). Terence observes Stella crossing the finish-line clock at t = 600.00 s. But Stella observes the time on her ship chronometer to be t′ = (t − vx/c) = 519.62 s as she passes the finish line, and she calculates the distance between the starting and finish lines, as measured in her frame, to be 259.81 light-seconds (about 77.9×10 km). 1).
Deriving the Lorentz transformations
Main article: Derivations of the Lorentz transformations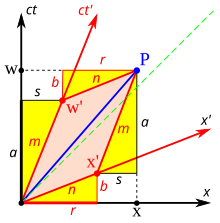
There have been many dozens of derivations of the Lorentz transformations since Einstein's original work in 1905, each with its particular focus. Although Einstein's derivation was based on the invariance of the speed of light, there are other physical principles that may serve as starting points. Ultimately, these alternative starting points can be considered different expressions of the underlying principle of locality, which states that the influence that one particle exerts on another can not be transmitted instantaneously.
The derivation given here and illustrated in Fig. 3‑5 is based on one presented by Bais and makes use of previous results from the Relativistic Composition of Velocities, Time Dilation, and Length Contraction sections. Event P has coordinates (w, x) in the black "rest system" and coordinates (w′, x′) in the red frame that is moving with velocity parameter β = v/c. How do we determine w′ and x′ in terms of w and x? (Or the other way around, of course.)
It is easier at first to derive the inverse Lorentz transformation.
- We start by noting that there can be no such thing as length expansion/contraction in the transverse directions. y' must equal y and z′ must equal z, otherwise whether a fast moving 1 m ball could fit through a 1 m circular hole would depend on the observer. The first postulate of relativity states that all inertial frames are equivalent, and transverse expansion/contraction would violate this law.
- From the drawing, w = a + b and x = r + s
- From previous results using similar triangles, we know that s/a = b/r = v/c = β.
- We know that because of time dilation, a = γw′
- Substituting equation (4) into s/a = β yields s = γw′β.
- Length contraction and similar triangles give us r = γx′ and b = βr = βγ'x′
- Substituting the expressions for s, a, r and b into the equations in Step 2 immediately yield
The above equations are alternate expressions for the t and x equations of the inverse Lorentz transformation, as can be seen by substituting ct for w, ct′ for w′, and v/c for β. From the inverse transformation, the equations of the forwards transformation can be derived by solving for t′ and x′.
Linearity of the Lorentz transformations
The Lorentz transformations have a mathematical property called linearity, since x' and t' are obtained as linear combinations of x and t, with no higher powers involved. The linearity of the transformation reflects a fundamental property of spacetime that we tacitly assumed while performing the derivation, namely, that the properties of inertial frames of reference are independent of location and time. In the absence of gravity, spacetime looks the same everywhere. All inertial observers will agree on what constitutes accelerating and non-accelerating motion. Any one observer can use her own measurements of space and time, but there is nothing absolute about them. Another observer's conventions will do just as well.
A result of linearity is that if two Lorentz transformations are applied sequentially, the result is also a Lorentz transformation.
Example: Terence observes Stella speeding away from him at 0.500 c, and he can use the Lorentz transformations with β = 0.500 to relate Stella's measurements to his own. Stella, in her frame, observes Ursula traveling away from her at 0.250 c, and she can use the Lorentz transformations with β = 0.250 to relate Ursula's measurements with her own. Because of the linearity of the transformations and the relativistic composition of velocities, Terence can use the Lorentz transformations with β = 0.666 to relate Ursula's measurements with his own.
Doppler effect
Main articles: Doppler effect and Relativistic Doppler effectClick here for a brief section summary
The Doppler effect is the change in frequency or wavelength of a wave for a receiver and source in relative motion. For simplicity, we consider here two basic scenarios: (1) The motions of the source and/or receiver are exactly along the line connecting them (longitudinal Doppler effect), and (2) the motions are at right angles to the said line (transverse Doppler effect). We are ignoring scenarios where they move along intermediate angles.
Longitudinal Doppler effect
The classical Doppler analysis deals with waves that are propagating in a medium, such as sound waves or water ripples, and which are transmitted between sources and receivers that are moving towards or away from each other. The analysis of such waves depends on whether the source, the receiver, or both are moving relative to the medium. Given the scenario where the receiver is stationary with respect to the medium, and the source is moving directly away from the receiver at a speed of vs for a velocity parameter of βs, the wavelength is increased, and the observed frequency f is given by
On the other hand, given the scenario where source is stationary, and the receiver is moving directly away from the source at a speed of vr for a velocity parameter of βr, the wavelength is not changed, but the transmission velocity of the waves relative to the receiver is decreased, and the observed frequency f is given by
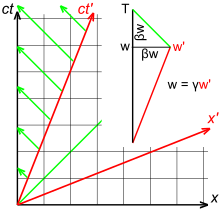
Light, unlike sound or water ripples, does not propagate through a medium, and there is no distinction between a source moving away from the receiver or a receiver moving away from the source. Fig. 3‑6 illustrates a relativistic spacetime diagram showing a source separating from the receiver with a velocity parameter β, so that the separation between source and receiver at time w is βw. Because of time dilation, w = γw'. Since the slope of the green light ray is −1, T = w+βw = γw'(1+β). Hence, the relativistic Doppler effect is given by
Transverse Doppler effect

Suppose that a source, moving in a straight line, is at its closest point to the receiver. It would appear that the classical analysis predicts that the receiver detects no Doppler shift. Due to subtleties in the analysis, that expectation is not necessarily true. Nevertheless, when appropriately defined, transverse Doppler shift is a relativistic effect that has no classical analog. The subtleties are these:
- Fig. 3-7a. If a source, moving in a straight line, is crossing the receiver's field of view, what is the frequency measurement when the source is at its closest approach to the receiver?
- Fig. 3-7b. If a source is moving in a straight line, what is the frequency measurement when the receiver sees the source as being closest to it?
- Fig. 3-7c. If receiver is moving in a circle around the source, what frequency does the receiver measure?
- Fig. 3-7d. If the source is moving in a circle around the receiver, what frequency does the receiver measure?
In scenario (a), when the source is closest to the receiver, the light hitting the receiver actually comes from a direction where the source had been some time back, and it has a significant longitudinal component, making an analysis from the frame of the receiver tricky. It is easier to make the analysis from S', the frame of the source. The point of closest approach is frame-independent and represents the moment where there is no change in distance versus time (i.e. dr/dt = 0 where r is the distance between receiver and source) and hence no longitudinal Doppler shift. The source observes the receiver as being illuminated by light of frequency f', but also observes the receiver as having a time-dilated clock. In frame S, the receiver is therefore illuminated by blueshifted light of frequency
Scenario (b) is best analyzed from S, the frame of the receiver. The illustration shows the receiver being illuminated by light from when the source was closest to the receiver, even though the source has moved on. Because the source's clocks are time dilated, and since dr/dt was equal to zero at this point, the light from the source, emitted from this closest point, is redshifted with frequency
Scenarios (c) and (d) can be analyzed by simple time dilation arguments. In (c), the receiver observes light from the source as being blueshifted by a factor of , and in (d), the light is redshifted. The only seeming complication is that the orbiting objects are in accelerated motion. However, if an inertial observer looks at an accelerating clock, only the clock's instantaneous speed is important when computing time dilation. (The converse, however, is not true.) Most reports of transverse Doppler shift refer to the effect as a redshift and analyze the effect in terms of scenarios (b) or (d).
Energy and momentum
Main articles: Four-momentum, Momentum, and Mass–energy equivalenceClick here for a brief section summary
Extending momentum to four dimensions

In classical mechanics, the state of motion of a particle is characterized by its mass and its velocity. Linear momentum, the product of a particle's mass and velocity, is a vector quantity, possessing the same direction as the velocity: p = mv. It is a conserved quantity, meaning that if a closed system is not affected by external forces, its total linear momentum cannot change.
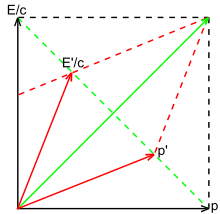
In relativistic mechanics, the momentum vector is extended to four dimensions. Added to the momentum vector is a time component that allows the spacetime momentum vector to transform like the spacetime position vector (x, t). In exploring the properties of the spacetime momentum, we start, in Fig. 3‑8a, by examining what a particle looks like at rest. In the rest frame, the spatial component of the momentum is zero, i.e. p = 0, but the time component equals mc.
We can obtain the transformed components of this vector in the moving frame by using the Lorentz transformations, or we can read it directly from the figure because we know that (mc)' = γmc and p' = −βγmc, since the red axes are rescaled by gamma. Fig. 3‑8b illustrates the situation as it appears in the moving frame. It is apparent that the space and time components of the four-momentum go to infinity as the velocity of the moving frame approaches c.
We will use this information shortly to obtain an expression for the four-momentum.
Momentum of light
Light particles, or photons, travel at the speed of c, the constant that is conventionally known as the speed of light. This statement is not a tautology, since many modern formulations of relativity do not start with constant speed of light as a postulate. Photons therefore propagate along a light-like world line and, in appropriate units, have equal space and time components for every observer.
A consequence of Maxwell's theory of electromagnetism is that light carries energy and momentum, and that their ratio is a constant: E/p = c. Rearranging, E/c = p, and since for photons, the space and time components are equal, E/c must therefore be equated with the time component of the spacetime momentum vector.
Photons travel at the speed of light, yet have finite momentum and energy. For this to be so, the mass term in γmc must be zero, meaning that photons are massless particles. Infinity times zero is an ill-defined quantity, but E/c is well-defined.
By this analysis, if the energy of a photon equals E in the rest frame, it equals E' = (1 − β)γE in a moving frame. This result can by derived by inspection of Fig. 3‑9 or by application of the Lorentz transformations, and is consistent with the analysis of Doppler effect given previously.
Mass-energy relationship
Consideration of the interrelationships between the various components of the relativistic momentum vector led Einstein to several famous conclusions.
- In the low speed limit as β = v/c approaches zero, approaches 1, so the spatial component of the relativistic momentum βγmc = γmv approaches mv, the classical term for momentum. Following this perspective, γm can be interpreted as a relativistic generalization of m. Einstein proposed that the relativistic mass of an object increases with velocity according to the formula mrel = γm.
- Likewise, comparing the time component of the relativistic momentum with that of the photon, γmc = mrelc = E/c, so that Einstein arrived at the relationship E = mrelc. Simplified to the case of zero velocity, this is Einstein's famous equation relating energy and mass.
Another way of looking at the relationship between mass and energy is to consider a series expansion of γmc at low velocity:
The second term is just an expression for the kinetic energy of the particle. Mass indeed appears to be another form of energy.
The concept of relativistic mass that Einstein introduced in 1905, mrel, although amply validated every day in particle accelerators around the globe (or indeed in any instrumentation whose use depends on high velocity particles, such as electron microscopes, old-fashioned color television sets, etc.), has nevertheless not proven to be a fruitful concept in physics in the sense that it is not a concept that has served as a basis for other theoretical development. Relativistic mass, for instance, plays no role in general relativity.
For this reason, as well as for pedagogical concerns, most physicists currently prefer a different terminology when referring to the relationship between mass and energy. "Relativistic mass" is a deprecated term. The term "mass" by itself refers to the rest mass or invariant mass, and is equal to the invariant length of the relativistic momentum vector. Expressed as a formula,
This formula applies to all particles, massless as well as massive. For massless photons, it yields the same relationship that we had earlier established, E = ±pc.
- ^ Morin, David (2017). Special Relativity for the Enthusiastic Beginner. CreateSpace Independent Publishing Platform. ISBN 9781542323512.
- Landau, L. D.; Lifshitz, E. M. (2006). The Classical Theory of Fields, Course of Theoretical Physics, Volume 2 (4th ed.). Amsterdam: Elsevier. pp. 1–24. ISBN 9780750627689.
- ^ Cite error: The named reference
Baiswas invoked but never defined (see the help page). - Cite error: The named reference
Schutzwas invoked but never defined (see the help page). - Rose, H. H. (21 April 2008). "Optics of high-performance electron microscopes". Science and Technology of Advanced Materials. 9 (1): 014107. Bibcode:2008STAdM...9a4107R. doi:10.1088/0031-8949/9/1/014107. Retrieved 4 July 2017.
- Griffiths, David J. (2013). Revolutions in Twentieth-Century Physics. Cambridge: Cambridge University Press. p. 60. ISBN 9781107602175. Retrieved 24 May 2017.
Cite error: There are <ref group=note> tags on this page, but the references will not show without a {{reflist|group=note}} template (see the help page).



 and so forth, we most often really mean
and so forth, we most often really mean 
 and so forth. Although, for brevity, we write the Lorentz transformation equations without deltas, it should be understood that x means Δx, etc. We are, in general, always concerned with the space and time differences between events.
and so forth. Although, for brevity, we write the Lorentz transformation equations without deltas, it should be understood that x means Δx, etc. We are, in general, always concerned with the space and time differences between events.
 (t − vx/c) = 519.62 s as she passes the finish line, and she calculates the distance between the starting and finish lines, as measured in her frame, to be 259.81 light-seconds (about 77.9×10 km).
1).
(t − vx/c) = 519.62 s as she passes the finish line, and she calculates the distance between the starting and finish lines, as measured in her frame, to be 259.81 light-seconds (about 77.9×10 km).
1).









