This is an old revision of this page, as edited by 213.130.5.38 (talk) at 14:51, 29 January 2005 (+uk). The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.
Revision as of 14:51, 29 January 2005 by 213.130.5.38 (talk) (+uk)(diff) ← Previous revision | Latest revision (diff) | Newer revision → (diff)In computer science, a linked list is one of the fundamental data structures used in computer programming. It consists of a sequence of nodes, each containing arbitrary data fields and one or two references ("links") pointing to the next and/or previous nodes. A linked list is called a self-referential datatype because it contains a pointer or link to another data of the same type. Linked lists permit insertion and removal of nodes at any point in the list in constant time, but do not allow random access. Several different types of linked list exist: single linked lists, double linked lists and circular linked lists.
Linked lists are most closely related to arrays, however a linked list has certain advantages over an array: it is easier to insert and delete nodes into a linked list than it is to an array, and you do not need to know ahead of time how much memory is needed as this can be determined at the point a node is inserted. An array does have advantages over a linked list: because you must recurse (or step through) every node in a linked list until an nth node is found, an array is much faster at this sort of operation because it can directly access data based on an array index.
Linked lists can be implemented in most languages. Lisp and Scheme have the data structure built in, along with operations to access the linked list. Languages such as C and C++ rely on pointers and memory addressing to create linked lists.
History
Linked lists were originally proposed by Maurice Wilkes when he introduced a "link field" to his arrays, which basically consisted of a pointer to the next record. These he called "lists". In 1964 he wrote a paper "Lists and Why They are Useful" which explained "in an expository manner what goes on in the computer memory when list-processing operations are performed, and takes as an example the formal differentiation of an algebraic expressions written in Polish notation".
LISP, standing for list processor, was created by John McCarthy in 1958 while he was at MIT and in 1960 he published its design in a paper in the Communications of the ACM, entitled "Recursive Functions of Symbolic Expressions and Their Computation by Machine, Part I". One of LISP's major data structures is the linked list. Wilkes also experimented with linked lists in languages and in 1964 produced the paper "An Experiment with a Self-compiling Compiler for a Simple List-Processing Language".
Variants
Singly-linked list
The simplest kind of linked list is a singly linked list (or slist for short), which has one link per node. This link points to the next node in the list, or to a null value or empty list if it is the last node.
A singly linked list containing three integer values
Doubly-linked list
A more sophisticated kind of linked list is a doubly linked list. Each node has two links, one to the previous node and one to the next.

An example of a doubly linked list.
In some very low level languages, Xor-linking offers a way to implement doubly-linked lists using a single word for both links, although the use of this technique is usually discouraged.
Circular list
In a circularly linked list, the first and last nodes are linked together. This can be done for both singly and doubly linked lists. To traverse a circular linked list, you begin at any node and follow the list in either direction until you return to the original node.
Singly linked lists are often handled by giving the address of the last element — because that element also provides quick access to the first one, whereas the converse is not true.
Sentinel nodes
Linked lists sometimes have a special dummy or sentinel node at the beginning and/or at the end of the list, which is not used to store data. Its purpose is to simplify or speed up some operations, by ensuring that every data node always has a previous and/or next node, and that every list (even one that contains no data elements) always has a "first" and "last" node.
Applications of linked lists
Linked lists are used as a building block for many other data structures, such as stacks, queues and their variations.
The "data" field of a node can be another linked list. By this device, one can construct many linked data structures with lists; this practice originated in the Lisp programming language, where linked lists are a primary (though by no means the only) data structure, and is now a common feature of the functional programming style.
Sometimes, linked lists are used to implement associative arrays, and are in this context called association lists. There is very little good to be said about this use of linked lists; they are easily outperformed by other data structures such as self-balancing binary search trees even on small data sets (see the discussion in associative array). However, sometimes a linked list is dynamically created out of a subset of nodes in such a tree, and used to more efficiently traverse that set.
Tradeoffs
As with most choices in computer programming and design, no method is well suited to all circumstances. A linked list data structure might work well in one case, but cause problems in another. This is a list of some of the common tradeoffs involving linked list structures. In general, if you have a dynamic collection, where elements are frequently being added and deleted, and the location of new elements added to the list is significant, then benefits of a linked list increase.
Linked lists vs. arrays
| Array | Linked list | |
|---|---|---|
| Indexing | O(1) | O(n) |
| Inserting | O(n) | O(1) |
| Deleting | O(n) | O(1) |
| Persistent | No | Singly yes |
| Locality | Great | Bad |
Linked lists have several advantages over arrays. They allow a new element to be inserted or deleted at any position in a constant number of operations (changing some references), while arrays require a linear (O(n)) number of operations. Elements can also be inserted into linked lists indefinitely, while an array will eventually either fill up or need to be resized, an expensive operation that may not even be possible if memory is fragmented. Similarly, an array from which many elements are removed may become wastefully empty or need to be made smaller.
Further memory savings can be achieved, in certain cases, by sharing the same "tail" of elements among two or more lists — that is, the lists end in the same sequence of elements. In this way, one can add new elements to the front of the list while keeping a reference to both the new and the old versions — a simple example of a persistent data structure.
On the other hand, arrays allow random access, while linked lists allow only sequential access to elements. Singly-linked lists, in fact, can only be traversed in one direction. This makes linked lists unsuitable for applications where it's useful to look up an element by its index quickly, such as heapsort. Sequential access on arrays is also faster than on linked lists on many machines due to locality of reference and data caches. Linked lists receive almost no benefit from the cache.
Another disadvantage of linked lists is the extra storage needed for references, which often makes them impractical for lists of small data items such as characters or boolean values. It can also be slow, and with a naïve allocator, wasteful, to allocate memory separately for each new element, a problem generally solved using memory pools.
A number of linked list variants exist that aim to ameliorate some of the above problems. Unrolled linked lists store several elements in each list node, increasing cache performance while decreasing memory overhead for references. CDR coding does both these as well, by replacing references with the actual data referenced, which extends off the end of the referencing record.
A good example that highlights the pros and cons of using arrays vs. linked lists is by implementing a program that resolves the Josephus problem. The Josephus problem is an election method that works by having a group of people stand in a circle. Starting at a pretermined person, you count around the circle n times. Once you reach nth person, take them out of the circle and have the members close the circle. Then count around the circle the same n times and repeat the process, until only one person is left. That person wins the election. This shows the strengths and weaknesses of a linked list vs. an array, because if you view the people as connected nodes in a circular linked list then it shows how easily the linked list is able to delete nodes (as it only has to rearrange the links to the different nodes). However, the linked list will be poor at finding the next person to remove and will need to recurse through the list till it finds that person. An array, on the other hand, will be poor at deleting nodes (or elements) as it cannot remove one node without individually shifting all the elements up the list by one. However, it is exceptionally easy to find the nth person in the circle by directly referencing them by their position in the array.
Double-linking vs. single-linking
Double-linked lists require more space per node (unless one uses xor-linking), and their elementary operations are more expensive; but they are often easier to manipulate because they allow sequential access to the list in both directions. In particular, one can insert or delete a node in a constant number of operations given only that node's address. Some algorithms require access in both directions. On the other hand, they do not allow tail-sharing, and cannot be used as persistent data structures.
Circular lists
Circular linked lists are most useful for describing naturally circular structures, and have the advantage of regular structure and being able to traverse the list starting at any point. They also allow quick access to the first and last records through a single pointer (the address of the last element). Their main disadvantage is the complexity of iteration, which has subtle special cases.
Sentinel nodes
Sentinel nodes may simplify certain list operations, by ensuring that the next and/or previous nodes exist for every element. However sentinel nodes use up extra space (especially in applications that use many short lists), and they may complicate other operations. To avoid the extra space requirement the sentinel nodes can often be reused as head and/or tail pointers.
Linked list operations
When manipulating linked lists in-place, care must be taken to not use values that you have invalidated in previous assignments. This makes algorithms for inserting or deleting linked list nodes somewhat subtle. This section gives pseudocode for adding or removing nodes from singly, doubly, and circularly linked lists in-place. Throughout we will use null to refer to an end-of-list marker or sentinel, which may be implemented in a number of ways.
Singly-linked lists
Our node data structure will have two fields. We also keep a variable head which always points to the first node in the list, or is null for an empty list.
record Node {
data // The data being stored in the node; often a reference to the actual data
next // A reference to the next node
}
Node head // points to front of list
Node nodeBeingRemoved // used in later examples
Traversal of a singly-linked list is easy, beginning at the first node and following each next link until we come to the end:
node := head // start at front of list
while node not null { // loop through list
(do something with node.data)
node := node.next // go to next node in list
}
The following code inserts a node after an existing node in a singly linked list. The diagram shows how it works. Inserting a node before an existing one cannot be done; instead, you have to locate it while keeping track of the previous node.
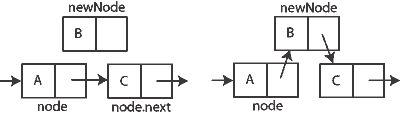
function insertAfter(Node node, Node newNode) { // insert newNode after node
newNode.next := node.next // point new node to next node
node.next := newNode // add new node to list
}
Inserting at the beginning of the list requires a separate function. This requires updating head.
function insertBeginning(Node newNode) { // insert node before current head
newNode.next := head // point to rest of list
head := newNode // new front of list
}
Similarly, we have functions for removing the node after a given node, and for removing a node from the beginning of the list. The diagram demonstrates the former. To find and remove a particular node, one must again keep track of the previous element.
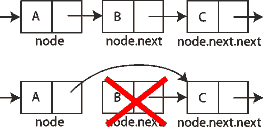
function removeAfter(Node node) { // remove node past this one
nodeBeingRemoved := node.next // this is the node to delete
node.next := node.next.next // point past node
(the above statement could be node.next = nodeBeingRemoved.next)
destroy nodeBeingRemoved // free up deleted node
}
function removeBeginning(Node node) { // remove head node
nodeBeingRemoved := head // this is the node to delete
head := head.next // point past deleted node
destroy nodeBeingRemoved // free up deleted node
}
Notice that removeBeginning() sets head to null when removing the last node in the list.
Doubly-linked lists
With doubly-linked lists there are even more pointers to update, but also less information is needed, since we can use backwards pointers to observe preceding elements in the list. This enables new operations, and eliminates special-case functions. We will add a prev field to our nodes, pointing to the previous element, and a tail variable which always points to the last node in the list. Both head and tail are null for an empty list.
Iterating through a doubly linked list can be done in either direction. In fact, direction can change many times, if desired.
Forwards
node := head
while node ≠ null
<do something with node.data>
node := node.next
Backwards
node := tail
while node ≠ null
<do something with node.data>
node := node.prev
These symmetric functions add a node either after or before a given node, with the diagram demonstrating after:

function insertAfter(node, newNode)
newNode.prev := node
newNode.next := node.next
if node.next = null
tail := newNode
else
node.next.prev := newNode
node.next := newNode
function insertBefore(node, newNode)
newNode.prev := node.prev
newNode.next := node
if node.prev is null
head := newNode
else
node.prev.next := newNode
node.prev := newNode
We also need a function to insert a node at the beginning of a possibly-empty list:
function insertBeginning(newNode)
if head = null
head := newNode
tail := newNode
newNode.prev := null
newNode.next := null
else
insertBefore(head, newNode)
A symmetric function inserts at the end:
function insertEnd(newNode)
if tail = null
insertBeginning(newNode)
else
insertAfter(tail, newNode)
Removing a node is easier, only requiring care with head and tail:
function remove(node)
if node.prev = null
head = node.next
else
node.prev.next = node.next
if node.next = null
tail := node.prev
else
node.next.prev = node.prev
destroy node
One subtle consequence of this procedure is that deleting the last element of a list sets both head and tail to null.
Circularly-linked lists
Circularly-linked lists can be either singly or doubly linked. In a circularly linked list, all nodes are linked in a continuous circle, without using null. For lists with a front and a back (such as a queue), one stores a reference to the last node in the list. The next node after the last node is the first node. Elements can be added to the back of the list and removed from the front in constant time.
Both types of circularly-linked lists benefit from the ability to traverse the full list beginning at any given node. This often allows us to avoid storing head and tail, although if the list may be empty we need a special representation for the empty list, such as a head variable which points to some node in the list or is null if it's empty; we use such a head here. This representation significantly simplifies adding and removing nodes with a non-empty list, but empty lists are then a special case.
Assuming that someNode is some node in a non-empty list, this code iterates through that list starting with someNode:
Forwards
node := someNode
do
do something with node.value
node := node.next
while node &neq; someNode
Backwards
node := someNode
do
do something with node.value
node := node.prev
while node &neq; someNode
Notice the postponing of the test to the end of the loop. This is important for the case where the list contains only the single node someNode.
This simple function inserts a node into a doubly-linked circularly linked list after a given element:
function insertAfter(node, newNode)
newNode.next := node.next
newNode.prev := node
node.next.prev := newNode
node.next := newNode
Inserting an element in a possibly empty list requires a special function:
function insertBeginning(node)
if head = null
node.prev := node
node.next := node
else
insertAfter(head.prev, node)
head := node
Finally, removing a node must deal with the case where the list empties:
function remove(node)
if node.next = node
head := null
else
node.next.prev := node.prev
node.prev.next := node.next
destroy node
Linked lists using arrays of nodes
Languages that don't support any type of reference can still create links by replacing pointers with array indices. The approach is to keep an array of records, where each record has integer fields indicating the index of the next and (possibly) previous node in the array. Not all nodes in the array need be used. If even records are not supported, parallel arrays can often be used instead.
As an example, consider the following linked list record that uses arrays instead of pointers:
record Entry {
integer next; // location of next entry in array
integer prev; // previous entry (if double-linked)
string Name; // Name on account
real balance; // Account balance
}
By creating an array of these structures, and an integer variable to store the index of the head element, a linked list can be built:
integer listHead; Entry Records;
Links between elements are formed by placing the array index of the next (or previous) cell into the Next or Prev field within a given element. For example:
| Index | Next | Prev | Name | Balance |
|---|---|---|---|---|
| 0 | 1 | 4 | Jones, John | 123.45 |
| 1 | -1 | 0 | Smith, Joseph | 234.56 |
| 2 | 4 | -1 | Adams, Adam | 0.00 |
| 3 | Ignore, Ignatius | 999.99 | ||
| 4 | 0 | 2 | Another, Anita | 876.54 |
| 5 | ||||
| 6 | ||||
| 7 |
In the above example, ListHead would be set to 4, the location of the first entry in the list. Notice that entry 3 and 5 through 7 are not part of the list. These cells are available for any additions to the list. By creating a ListFree integer variable, a free list could be created to keep track of what cells are available. If all entries are in use, the size of the array would have to be increased or some elements would have to be deleted before new entries can be stored in the list.
The following code would traverse the list and display names and account balance:
i := listHead; // start at beginning of list
while i >= 0 { '// loop through the list
print i, Records.name, Records.balance // print entry
i = Records.next; // next entry in list
}
When faced with a choice, the advantages of this approach include:
- The linked list is relocatable, meaning it can be moved about in memory at will, and it can also be quickly and directly serialized for storage on disk or transfer over a network.
- Especially for a small list, array indexes can occupy significantly less space than a full pointer on many architectures.
- Locality of reference can be improved by keeping the nodes together in memory and by periodically rearranging them, although this can also be done in a general store.
- Naïve dynamic memory allocators can produce an excessive amount of overhead storage for each node allocated; almost no allocation overhead is incurred per node in this approach.
This approach has one main disadvantage, however: it creates and manages a private memory space for its nodes. Not only does this increase complexity of the implementation, but growing it may be difficult or impossible, because it is large, whereas finding space for a new linked list node in a large, general memory pool is easier. This slow growth also affects algorithmic performance, as it causes a few insert operations to unexpectedly take linear (O(n)) instead of constant time (although it's still amortized constant). Using a general memory pool also leaves more memory for other data if the list is smaller than expected or if many nodes are freed. However, since this approach is mainly used for languages that do not support dynamic memory allocation, the block of memory is created at compile / load time, this is usually not an issue.
Language support
Many programming languages such as Lisp and Scheme have singly linked lists built in. In many functional languages, these lists are constructed from nodes, each called a cons or cons cell. The cons has two fields: the car, a reference to the data for that node, and the cdr, a reference to the next node. Although cons cells can be used to build other data structures, this is their primary purpose.
In other languages, linked list are typically built using references together with records. Here is a complete example in C:
#include <stdio.h> /* for printf */
#include <stdlib.h> /* for malloc */
typedef struct ns {
int data;
struct ns *next;
} node;
node *list_add(node ** p, int i) {
node *n = malloc(sizeof(*n));
n->next = *p;
*p = n;
n->data = i;
return n;
}
void list_remove(node ** p) {
if (p) {
node *n = *p;
*p = (*p)->next;
free(n);
}
}
node **list_search(node ** n, int i) {
if (!n) return NULL;
while (*n) {
if ((*n)->data == i) {
return n;
}
n = &(*n)->next;
}
return NULL;
}
void list_print(node * n) {
if (!n) printf("list is empty\n");
while (n) {
printf("print %p %p %i \n", n, n->next, n->data);
n = n->next;
}
}
int main(void) {
node *n = NULL;
list_add(&n, 0);
list_add(&n, 1);
list_add(&n, 2);
list_add(&n, 3);
list_add(&n, 4);
list_print(n);
list_remove(&n); /* remove head */
list_remove(&n->next); /* remove second */
list_remove(list_search(&n, 1));
list_remove(&n->next); /* remove tail */
list_remove(&n); /* remove last */
list_print(n);
return 0;
}
Internal and external storage
When constructing a linked list, one is faced with the choice of whether to store the data of the list directly in the linked list nodes, called internal storage, or to merely store a reference to the data, called external storage. Internal storage has the advantage of making access to the data more efficient, requiring less storage overall, having better locality of reference, and simplifying memory management for the list (its data is allocated and deallocated at the same time as the list nodes).
External storage, on the other hand, has the advantage of being more generic, in that the same data structure and machine code can be used for a linked list no matter what the size of the data is. It also makes it easy to place the same data in multiple linked lists. Note, however, that even with internal storage the same data can be placed in multiple lists, either by including multiple next references in the node data structure, or by having other linked lists store references to the nodes of the linked list containing the data.
A common misconception is that every list using internal storage requires a new set of functions to operate on the linked list, consuming more effort and code space than an approach using external storage. This is true with a naïve approach, but as long as the next pointers are located in the same place in each record, it is possible to create a generic implementation of linked lists with internal storage that only needs to be supplied for each type of list a way of creating and destroying nodes.
Example
Suppose you wanted to create a linked list of families and their members. Using internal storage, the structure might look like the following:
record member { // structure for a member of a family
member next // pointer to other members of family
string fname // first name
integer age // age of member
}
record family { // structure for the family itself
family next // pointer to other families
string lname // last name of family
string address // address of family
string phone // phone number of family
member members // pointer to list of members of family
}
To print a complete list of families and their members using internal storage, we could write:
aFamily := Families // start at head of list
while aFamily ≠ null { // loop through list of families
print information about family
aMember := aFamily.members // get list of family members
while aMember ≠ null { // loop through list of members
print information about member
aMember := aMember.next // go to next member
}
aFamily := aFamily.next // go to next family
}
Using external storage, we would create the following structures:
record node { // generic link structure
node next // pointer to next node
pointer data // generic pointer for data at node
}
record member { // structure for family member
string fname // first name
integer age // age of member
}
record family { // structure for family
string lname // last name of family
string address // address of family
string phone // phone number of family
node members // pointer to list of members of family
}
To print a complete list of families and their members using external storage, we could write:
famNode := Families // start at head of list
while famNode ≠ null { // loop through list of families
aFamily = (family)famNode.data // extract family from node
print information about family
memNode := aFamily.members // get list of family members
while memNode ≠ null { // loop through list of members
aMember := (member)memNode.data // extract member from node
print information about member
memNode := memNode.next // get next family member
}
famNode := famNode.next // get next family in list
}
Notice that when using external storage, an extra step is needed to extract the record from the node and cast it into the proper data type.
Related data structures
The skip list is a linked list augmented with layers of pointers for quickly jumping over large numbers of elements, and then descending to the next layer. This process continues down to the bottom layer, which is the actual list.
A binary tree can be seen as a type of linked list where the elements are themselves linked lists of the same nature. The result is that each node may include a reference to the head node of one or two other linked lists, which, together with their contents, form the subtrees below that node.
An unrolled linked list is a linked list in which each node contains an array of data values. This leads to improved cache performance, since more list elements are contiguous in memory, and reduced memory overhead, because less metadata needs to be stored for each element of the list.
References
- National Institute of Standards and Technology (August 16, 2004). Definition of a linked list. Retrieved December 14, 2004.
- Antonakos, James L. and Mansfield, Kenneth C., Jr. Practical Data Structures Using C/C++ (1999). Prentice-Hall. ISBN 0-13-280843-9, pp. 165–190
- Collins, William J. Data Structures and the Java Collections Framework (2002,2005) New York, NY: McGraw Hill. ISBN 0-07-282379-8, pp. 239–303
- Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford Introductions to Algorithms (2003). MIT Press. ISBN 0-262-03293-7, pp. 205–213, 501–505
- McCarthy, John (1960). Recursive Functions of Symbolic Expressions and Their Computation by Machine, Part I. Communications of the ACM. HTML DVI PDF PostScript
- Parlante, Nick (2001). Linked list basics. Stanford University. PDF
- Sedgewick, Robert Algorithms in C (1998). Addison Wesley. ISBN 0-201-31452-5, pp. 90–109
- Shaffer, Clifford A. A Practical Introduction to Data Structures and Algorithm Analysis (1998). NJ: Prentice Hall. ISBN 0-13-660911-2, pp. 77–102
- Wilkes, Maurice Vincent (1964). An Experiment with a Self-compiling Compiler for a Simple List-Processing Language. Annual Review in Automatic Programming 4, 1. Published by Pergamon Press. TIFF format
- Wilkes, Maurice Vincent (1964). Lists and Why They are Useful. Proceeds of the ACM National Conference, Philadelphia 1964 (ACM Publication P-64 page F1-1); Also Computer Journal 7, 278 (1965).
External links
- Description from the Dictionary of Algorithms and Data Structures
- Some linked list materials are available from the Stanford University Computer Science department:
- Citations from CiteSeer