Misplaced Pages

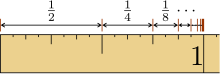
In mathematics, the infinite series ⁠1/2⁠ + ⁠1/4⁠ + ⁠1/8⁠ + ⁠1/16⁠ + ··· is an elementary example of a geometric series that converges absolutely. The sum of the series is 1. In summation notation, this may be expressed as

${\displaystyle {\frac {1}{2}}+{\frac {1}{4}}+{\frac {1}{8}}+{\frac {1}{16}}+\cdots =\sum _{n=1}^{\infty }\left({\frac {1}{2}}\right)^{n}=1.}$

The series is related to philosophical questions considered in antiquity, particularly to Zeno's paradoxes.

Proof

As with any infinite series, the sum

${\displaystyle {\frac {1}{2}}+{\frac {1}{4}}+{\frac {1}{8}}+{\frac {1}{16}}+\cdots }$

is defined to mean the limit of the partial sum of the first n terms

${\displaystyle s_{n}={\frac {1}{2}}+{\frac {1}{4}}+{\frac {1}{8}}+{\frac {1}{16}}+\cdots +{\frac {1}{2^{n-1}}}+{\frac {1}{2^{n}}}}$

as n approaches infinity, if it exists. By various arguments, one can show that each finite sum is equal to

${\displaystyle s_{n}=1-{\frac {1}{2^{n}}},}$

and as n approaches infinity, the term ${\displaystyle {\frac {1}{2^{n}}}}$ approaches 0 and so s_n approaches 1.

History

Zeno's paradox

This series was used as a representation of two of Zeno's paradoxes. For example, in the paradox of Achilles and the Tortoise, the warrior Achilles was to race against a tortoise. The track is 100 meters long. Achilles could run at 10 m/s, while the tortoise only 5. The tortoise, with a 10-meter advantage, Zeno argued, would win. Achilles would have to move 10 meters to catch up to the tortoise, but the tortoise would already have moved another five meters by then. Achilles would then have to move 5 meters, where the tortoise would move 2.5 meters, and so on. Zeno argued that the tortoise would always remain ahead of Achilles. Similarly, Zeno's dichotomy paradox arises from the supposition that to move a certain distance, one would have to move half of it, then half of the remaining distance, and so on, therefore having infinitely many time intervals.

In both cases, each time interval is a term of this infinite geometric series, and so even in the limit of infinite terms it would sum to a finite total time. This is sometimes considered to resolve Zeno's paradoxes. However, insofar as Zeno was concerned with the problems of division of a continuum into an actual infinity of sub-parts, rather than the problem of their sum, it may not address the philosophical heart of Zeno's argument.

The Eye of Horus

The parts of the Eye of Horus were once thought to represent the first six summands of the series.

In Zhuangzi

A version of the series appears in the ancient Taoist book Zhuangzi. The miscellaneous chapters "All Under Heaven" include the following sentence: "Take a chi long stick and remove half every day, in a myriad ages it will not be exhausted."

See also

• 0.999...
• 1/2 − 1/4 + 1/8 − 1/16 + ⋯
• Actual infinity

Notes

1. For example: multiplying s_n by 2 yields ${\displaystyle 2s_{n}={\frac {2}{2}}+{\frac {2}{4}}+{\frac {2}{8}}+{\frac {2}{16}}+\cdots +{\frac {2}{2^{n}}}=1+\left=1+\left.}$ Subtracting s_n from both sides, one concludes ${\displaystyle s_{n}=1-{\frac {1}{2^{n}}}.}$ Other arguments might proceed by mathematical induction, or by adding ${\displaystyle {\frac {1}{2^{n}}}}$ to both sides of ${\displaystyle s_{n}={\frac {1}{2}}+{\frac {1}{4}}+{\frac {1}{8}}+{\frac {1}{16}}+\cdots +{\frac {1}{2^{n-1}}}+{\frac {1}{2^{n}}}}$ and manipulating to show that the right side of the result is equal to 1.

References

1. Abramowitz, M.; Stegun, I. A., eds. (1972). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables (9th printing). New York: Dover. p. 10.
2. ^ Field, Paul and Weisstein, Eric W. "Zeno's Paradoxes." From MathWorld--A Wolfram Web Resource. https://mathworld.wolfram.com/ZenosParadoxes.html
3. Huggett, Nick (2010). "Zeno's Paradoxes: 5. Zeno's Influence on Philosophy". Stanford Encyclopedia of Philosophy. Archived from the original on 2022-03-01. Retrieved 2011-03-07.
4. Papa-Grimaldi, Alba (1996). "Why Mathematical Solutions of Zeno's Paradoxes Miss the Point: Zeno's One and Many Relation and Parmenides' Prohibition" (PDF). The Review of Metaphysics. 50: 299–314. Archived (PDF) from the original on 2012-06-09. Retrieved 2012-03-06.
5. Stewart, Ian (2009). Professor Stewart's Hoard of Mathematical Treasures. Profile Books. pp. 76–80. ISBN 978-1-84668-292-6.

v t e Sequences and series
Integer sequences	Basic Arithmetic progression Geometric progression Harmonic progression Square number Cubic number Factorial Powers of two Powers of three Powers of 10 Advanced (list) Complete sequence Fibonacci sequence Figurate number Heptagonal number Hexagonal number Lucas number Pell number Pentagonal number Polygonal number Triangular number array
Properties of sequences	Cauchy sequence Monotonic function Periodic sequence
Properties of series	Series Alternating Convergent Divergent Telescoping Convergence Absolute Conditional Uniform
Explicit series	Convergent 1/2 − 1/4 + 1/8 − 1/16 + ⋯ 1/2 + 1/4 + 1/8 + 1/16 + ⋯ 1/4 + 1/16 + 1/64 + 1/256 + ⋯ 1 + 1/2 + 1/3 + ... (Riemann zeta function) Divergent 1 + 1 + 1 + 1 + ⋯ 1 − 1 + 1 − 1 + ⋯ (Grandi's series) 1 + 2 + 3 + 4 + ⋯ 1 − 2 + 3 − 4 + ⋯ 1 + 2 + 4 + 8 + ⋯ 1 − 2 + 4 − 8 + ⋯ Infinite arithmetic series 1 − 1 + 2 − 6 + 24 − 120 + ⋯ (alternating factorials) 1 + 1/2 + 1/3 + 1/4 + ⋯ (harmonic series) 1/2 + 1/3 + 1/5 + 1/7 + 1/11 + ⋯ (inverses of primes)
Kinds of series	Taylor series Power series Formal power series Laurent series Puiseux series Dirichlet series Trigonometric series Fourier series Generating series
Hypergeometric series	Generalized hypergeometric series Hypergeometric function of a matrix argument Lauricella hypergeometric series Modular hypergeometric series Riemann's differential equation Theta hypergeometric series
Category

• Geometric series
• 1 (number)