| This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Limiting reagent" – news · newspapers · books · scholar · JSTOR (June 2015) (Learn how and when to remove this message) |
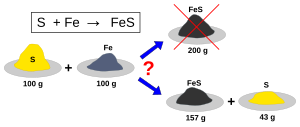
The limiting reagent (or limiting reactant or limiting agent) in a chemical reaction is a reactant that is totally consumed when the chemical reaction is completed. The amount of product formed is limited by this reagent, since the reaction cannot continue without it. If one or more other reagents are present in excess of the quantities required to react with the limiting reagent, they are described as excess reagents or excess reactants (sometimes abbreviated as "xs"), or to be in abundance.
The limiting reagent must be identified in order to calculate the percentage yield of a reaction since the theoretical yield is defined as the amount of product obtained when the limiting reagent reacts completely. Given the balanced chemical equation, which describes the reaction, there are several equivalent ways to identify the limiting reagent and evaluate the excess quantities of other reagents.
Method 1: Comparison of reactant amounts
This method is most useful when there are only two reactants. One reactant (A) is chosen, and the balanced chemical equation is used to determine the amount of the other reactant (B) necessary to react with A. If the amount of B actually present exceeds the amount required, then B is in excess and A is the limiting reagent. If the amount of B present is less than required, then B is the limiting reagent.
Example for two reactants
Consider the combustion of benzene, represented by the following chemical equation:
This means that 15 moles of molecular oxygen (O2) is required to react with 2 moles of benzene (C6H6)
The amount of oxygen required for other quantities of benzene can be calculated using cross-multiplication (the rule of three). For example, if 1.5 mol C6H6 is present, 11.25 mol O2 is required:
If in fact 18 mol O2 are present, there will be an excess of (18 - 11.25) = 6.75 mol of unreacted oxygen when all the benzene is consumed. Benzene is then the limiting reagent.
This conclusion can be verified by comparing the mole ratio of O2 and C6H6 required by the balanced equation with the mole ratio actually present:
- required:
- actual:
Since the actual ratio is larger than required, O2 is the reagent in excess, which confirms that benzene is the limiting reagent.
Method 2: Comparison of product amounts which can be formed from each reactant
In this method the chemical equation is used to calculate the amount of one product which can be formed from each reactant in the amount present. The limiting reactant is the one which can form the smallest amount of the product considered. This method can be extended to any number of reactants more easily than the first method.
Example
20.0 g of iron (III) oxide (Fe2O3) are reacted with 8.00 g aluminium (Al) in the following thermite reaction:
Since the reactant amounts are given in grams, they must be first converted into moles for comparison with the chemical equation, in order to determine how many moles of Fe can be produced from either reactant.
- Moles of Fe which can be produced from reactant Fe2O3
- Moles of Fe which can be produced from reactant Al
There is enough Al to produce 0.297 mol Fe, but only enough Fe2O3 to produce 0.250 mol Fe. This means that the amount of Fe actually produced is limited by the Fe2O3 present, which is therefore the limiting reagent.
Shortcut
It can be seen from the example above that the amount of product (Fe) formed from each reagent X (Fe2O3 or Al) is proportional to the quantity
This suggests a shortcut which works for any number of reagents. Just calculate this formula for each reagent, and the reagent that has the lowest value of this formula is the limiting reagent. We can apply this shortcut in the above example.
See also
References
- Olmsted, John; Williams, Gregory M. (1997). Chemistry: The Molecular Science. Jones & Bartlett Learning. p. 163. ISBN 0815184506.
- Zumdahl, Steven S. (2006). Chemical Principles (4th ed.). New York: Houghton Mifflin Company. ISBN 0-618-37206-7.
- Masterton, William L.; Hurley, Cecile N. (2008). Chemistry: Principles and Reactions (6 ed.). Cengage Learning. ISBN 978-0-495-12671-3.









