
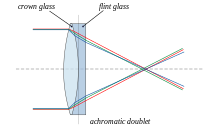

An achromatic lens or achromat is a lens that is designed to limit the effects of chromatic and spherical aberration. Achromatic lenses are corrected to bring two wavelengths (typically red and blue) into focus on the same plane. Wavelengths in between these two then have better focus error than could be obtained with a simple lens.
The most common type of achromat is the achromatic doublet, which is composed of two individual lenses made from glasses with different amounts of dispersion. Typically, one element is a negative (concave) element made out of flint glass such as F2, which has relatively high dispersion, and the other is a positive (convex) element made of crown glass such as BK7, which has lower dispersion. The lens elements are mounted next to each other, often cemented together, and shaped so that the chromatic aberration of one is counterbalanced by that of the other.
In the most common type (shown), the positive power of the crown lens element is not quite equalled by the negative power of the flint lens element. Together they form a weak positive lens that will bring two different wavelengths of light to a common focus. Negative doublets, in which the negative-power element predominates, are also made.
History
Theoretical considerations of the feasibility of correcting chromatic aberration were debated in the 18th century following Newton's statement that such a correction was impossible (see History of the telescope). Credit for the invention of the first achromatic doublet is often given to an English barrister and amateur optician named Chester Moore Hall. Hall wished to keep his work on the achromatic lenses a secret and contracted the manufacture of the crown and flint lenses to two different opticians, Edward Scarlett and James Mann. They in turn sub-contracted the work to the same person, George Bass. He realized the two components were for the same client and, after fitting the two parts together, noted the achromatic properties. Hall used the achromatic lens to build the first achromatic telescope, but his invention did not become widely known at the time.
In the late 1750s, Bass mentioned Hall's lenses to John Dollond, who understood their potential and was able to reproduce their design. Dollond applied for and was granted a patent on the technology in 1758, which led to bitter fights with other opticians over the right to make and sell achromatic doublets.
Dollond's son Peter invented the apochromat, an improvement on the achromat, in 1763.
Types
Several different types of achromat have been devised. They differ in the shape of the included lens elements as well as in the optical properties of their glass (most notably in their optical dispersion or Abbe number).
In the following, R denotes the radius of the spheres that define the optically relevant refracting lens surfaces. By convention, R1 denotes the first lens surface counted from the object. A doublet lens has four surfaces with radii R1 through R2 . Surfaces with positive radii curve away from the object (R1 positive is a convex first surface); negative radii curve toward the object (R1 negative is a concave first surface).
The descriptions of the achromat lens designs mention advantages of designs that do not produce "ghost" images. Historically, this was indeed a driving concern for lens makers up to the 19th century and a primary criterion for early optical designs. However, in the mid 20th century, the development of advanced optical coatings for the most part has eliminated the issue of ghost images, and modern optical designs are preferred for other merits.
Littrow doublet
Uses an equiconvex crown glass lens (i.e. R1 > 0 with −R1 = R2 ) and a complementary-curved second flint glass lens (with R3 = R2 ). The back of the flint glass lens is flat ( R4 = ∞ ). A Littrow doublet can produce a ghost image between R2 and R3 because the lens surfaces of the two lenses have the same radii.
Fraunhofer doublet (Fraunhofer objective)
The first lens has positive refractive power, the second negative. R1 > 0 is set greater than −R2 , and R3 is set close to, but not quite equal to, −R2 . R4 is usually greater than −R3 . In a Fraunhofer doublet, the dissimilar curvatures of −R2 and R3 are mounted close, but not quite in contact. This design yields more degrees of freedom (one more free radius, length of the air space) to correct for optical aberrations.
Clark doublet
Early Clark lenses follow the Fraunhofer design. After the late 1860s, they changed to the Littrow design, approximately equiconvex crown, R1 = R2 , and a flint with R3 ≃ R2 and R4 ≫ R3 . By about 1880, Clark lenses had R3 set slightly shorter than R2 to create a focus mismatch between R2 and R3, thereby avoiding ghosting caused by reflections within the airspace.
Oil-spaced doublet
The use of oil between the crown and flint eliminates the effect of ghosting, particularly where R2 ≈ R3 . It can also increase light transmission slightly and reduce the impact of errors in R2 and R3 .
Steinheil doublet
The Steinheil doublet, devised by Carl August von Steinheil, is a flint-first doublet. In contrast to the Fraunhofer doublet, it has a negative lens first followed by a positive lens. It needs stronger curvature than the Fraunhofer doublet.
Dialyte
Dialyte lenses have a wide air space between the two elements. They were originally devised in the 19th century to allow much smaller flint glass elements down stream since flint glass was hard to produce and expensive. They are also lenses where the elements can not be cemented because R2 and R3 have different absolute values.
Design
The first-order design of an achromat involves choosing the overall power of the doublet and the two glasses to use. The choice of glass gives the mean refractive index, often written as (for the refractive index at the Fraunhofer "d" spectral line wavelength), and the Abbe number (for the reciprocal of the glass dispersion). To make the linear dispersion of the system zero, the system must satisfy the equations
where the lens power is for a lens with focal length . Solving these two equations for and gives
- and
Since and the Abbe numbers are positive-valued, the power of the second element in the doublet is negative when the first element is positive, and vice-versa.
Removing other aberrations
Optical aberrations other than just color are present in all lenses. For example, coma remains after spherical and chromatic aberrations are corrected. In order to correct other aberrations, the front and back curvatures of each of the two lenses remain free parameters, since the color correction design only prescribes the net focal length of each lens, and separately This leaves a continuum of different combinations of front and back lens curvatures for design tweaks ( and for lens 1; and and for lens 2) that will all produce the same and required by the achromat design. Other adjustable lens parameters include the thickness of each lens and the space between the two, all constrained only by the two required focal lengths. Normally, the free parameters are adjusted to minimize non-color-related optical aberrations.
Further color correction

Lens designs more complex than achromatic can improve the precision of color images by bringing more wavelengths into exact focus, but require more expensive types of glass, and more careful shaping and spacing of the combination of simple lenses:
- apochromatic lenses
- bring three wavelengths into a common focus and requires costly materials
- superachromatic lenses
- bring four wavelengths into focus and must be manufactured with even more expensive fluoride glass and to considerably tighter tolerances
In theory, the process can continue indefinitely: Compound lenses used in cameras typically have six or more simple lenses (e.g. double-Gauss lens); several of those lenses can be made with different types of glass, with slightly altered curvatures, in order to bring more colors into focus. The constraint is extra manufacturing cost, and diminishing returns of improved image for the effort.
See also
References
- Daumas, Maurice, Scientific Instruments of the Seventeenth and Eighteenth Centuries and Their Makers, Portman Books, London 1989 ISBN 978-0-7134-0727-3
- ^ Watson, Fred (2007). Stargazer: the life and times of the telescope. Allen & Unwin. pp. 140–55. ISBN 978-1-74175-383-7.
- Fred Hoyle, Astronomy; A history of man's investigation of the universe, Rathbone Books, 1962, LCCN 62-14108
- J. A. B. "Peter Dollond answers Jesse Ramsden". Sphaera 8. Museum of the History of Science, Oxford. Retrieved November 27, 2017. – A review of the events of the invention of the achromatic doublet with emphasis on the roles of Hall, Bass, John Dollond and others.
- Dokland, Terje; Ng, Mary Mah-Lee (2006). Techniques in microscopy for biomedical applications. p. 23. ISBN 981-256-434-9.
- "Chester Moor Hall". Encyclopædia Britannica. Retrieved 16 February 2019.
- Wolfe, William L. (2007). Optics Made Clear: The nature of light and how We Use it. Press monograph. Vol. 163 (illustrated ed.). SPIE. p. 38. ISBN 9780819463074.
- Warner, Deborah Jean; Ariail, Robert B. (1995). Alvan Clark & Sons, Artists In Optics (2nd ed.). Willmann-Bell. p. 174.
- Kidger, M.J. (2002). Fundamental Optical Design. Bellingham, WA: SPIE Press. p. 174 ff.
- Manly, Peter L. (1995). Unusual Telescopes. Cambridge University Press. p. 55. ISBN 978-0-521-48393-3.
- Carson, Fred A. Basic Optics and Optical Instruments. p. AJ-4.
External links
 Media related to Achromatic lenses at Wikimedia Commons
Media related to Achromatic lenses at Wikimedia Commons
 of the doublet and the two glasses to use. The choice of glass gives the mean refractive index, often written as
of the doublet and the two glasses to use. The choice of glass gives the mean refractive index, often written as  (for the refractive index at the
(for the refractive index at the  (for the reciprocal of the glass
(for the reciprocal of the glass 
 for a lens with
for a lens with  . Solving these two equations for
. Solving these two equations for  and
and  gives
gives
 and
and 
 and the
and the  This leaves a continuum of different combinations of front and back lens curvatures for design tweaks (
This leaves a continuum of different combinations of front and back lens curvatures for design tweaks ( and
and  for lens 1; and
for lens 1; and  and
and  for lens 2) that will all produce the same
for lens 2) that will all produce the same