 | |
| Paradigm | Object-oriented, Prototype-oriented |
|---|---|
| Developer | Altarica Association |
| First appeared | 1998 |
| Stable release | 3.0 / 3.0 (2020) |
| OS | Cross-platform |
| License | Proprietary software |
| Filename extensions | .alt |
| Website | www |
| Major implementations | |
| Cecilia OCAS, Safety Designer, SIMFIA, AltaRica Wizard | |
| Influenced by | |
| Lustre7, Modellica | |
AltaRica is an object-oriented modeling language dedicated to probabilistic risk and safety analyses. It is a representative of the so-called model-based approach in reliability engineering. Since its version 3.0, it is developed by the non-profit AltaRica Association, which develops jointly the associated modeling environment AltaRica Wizard.
History
The design of AltaRica started at the end of the nineties at the computer science department of Bordeaux University (LaBRI). The rationale for the creation of a new modeling language was to overcome difficulties encountered by safety analysts (in avionic, nuclear, automotive and oil and gas industries) with "classical" modeling formalisms such as fault trees, Markov chains or stochastic Petri nets. These formalisms lack actually either of expressive power, or of structuring constructs, or both. The first scientific articles. about the language were published from 1998 to 2008. The original version of the language relied of three technologies: finite-state automata that were extensively studied by the LaBRI's team working of the formal methods for software verification, structured programming taking inspiration of the modeling language Lustre, and constraint programming. This last technology, though elegant and powerful, proved inefficient in practice. Constraint resolution was too computationally expensive to scale on industrial size systems. The LaBRI team went on working however on this original version, mainly for educational purposes, improving tools over the years. A first turn has been therefore taken with the design of a data-flow version of the language. In AltaRica data-flow, variables are updated by propagating values in a fixed order. This order is determined at compile time, from the annotations given in the model. AltaRica Data-Flow raised a significant academic and industrial interest. Integrated modeling environments have been developed for the language: Cecilia OCAS by Dassault Aviation, Simfia v2 by Airbus-Apsys and Safety Designer by Dassault Systèmes (this latter tool was initially a clone of Cecilia OCAS, but evolved separately afterward). Successful industrial applications have been realized. For example, AltaRica Data-Flow was used to certify the flight control system of the aircraft Falcon 7X (Dassault Aviation). A number of PhD theses were also dedicated to the language and its use in various contexts. In a word, AltaRica Data-Flow reached scientific and industrial maturity. It is still daily used for a wide variety of applications.
Experience showed however that AltaRica Data-Flow could be improved in several ways, hence justifying to seriously rework the language. This rework gave eventually raise to AltaRica 3.0 which improves AltaRica Data-Flow into several directions. The syntax of AltaRica 3.0 is closer to Modelica than to AltaRica data-flow, so to facilitate bridges between multiphysics modeling and simulation and probabilistic risk and safety analyses. Object-oriented and prototype-oriented structuring constructs have been assembled so to give the language a versatile and coherent set of structuring constructs, via S2ML (for System Structure Modeling Language), which is probably the most complete of all existing behavioral modeling languages. Moreover, AltaRica 3.0 semantics has been reinforced, via GTS (for Guarded Transition Systems), which opens new opportunities in terms of assessment of models.
Guarded transition systems
Guarded transition systems belong to the family of mathematical models of computation gathered under the generic term of (stochastic) finite-state automata. They have been introduced in 2008 and later refined
To illustrate the ideas behind guarded transition systems, consider a motor pump that is normally in stand-by, that can be started on demand and stopped when there is no more demand. Assume moreover that this pump may fail in operation, with a certain failure rate λ, and that it can also fail on-demand with a certain probability γ, Assume finally that the pump can be repaired, with a certain mean time to repair τ.
We can then represent the behavior of this pump by means of a (stochastic) finite state automaton pictured hereafter.
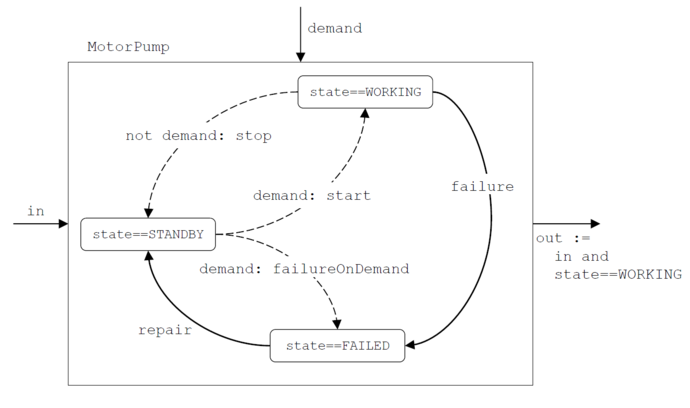
From outside, the motor pump can be seen as a black box with an input flow of liquid "in", an input flow of information "demand" and an output flow of liquid "out", i.e. as a transfer function that given the values "in" and "demand" calculates the value "out". In the framework on reliability studies, the behavior of systems must be abstracted out to avoid the combinatorial explosion of situations to look at. Flows are thus typically abstracted as Boolean values, true interpreted as the presence of the flow and false as its absence.
The equation linking "in" and "demand" to "out" cannot be written directly since the motor pump has an internal state. Namely, we can consider that the pump can be in three states: "STANDBY", "WORKING" or "FAILED". On the figure before, states are represented as rounded rectangle. The output flow "out" takes the value true if and only if the pump is working and the input flow "in" is true (hence the equation on the right hand side of the figure above).
A fundamental abstraction made by finite-state automata consists in considering that the system under study can change of state only under the occurrence of an event. In between two occurrences of events, nothing changes. Occurrences of events are described by means of transitions, represented as arrows on the figure. In guarded transition systems, a transition is labeled with an event, has a certain pre-condition called the guard of the transition and a certain effect called the action of the transition. For instance, the event "failure" can only occur in the state "WORKING". Its effect is to make the pump pass from this state "WORKING" to the state "FAILED". The event "start" can occur if the pump is in the state "STANDBY" and if the input flow "demand" is true. Its effect is to make the pump pass from the state "STANDBY" to the state "WORKING". And so on.
Now, some changes of states may take time, while some other happen as soon as they are possible. For instance, a failure takes a certain time before occurring, while the pump is started as soon as needed (at least at the level of abstraction of reliability models). Guarded transition systems associate delays with events, and thus transitions. These delays can be either deterministic as for the event "start", or stochastic as for the event "failure". On the figure, deterministic delays are represented by dashed arrows while stochastic ones are represented by plain arrows.
To finish, transitions can be in competition in a state. For instance, the transition "stop" is in competition with the transition "failure" in the state "WORKING". This competition is however not a real one as the transition "stop" is immediately fired (performed) when the input flow "demand" ceases to be true. A real competition occurs between the transitions "start" and "failureOnDemand" in the state "STANDBY". Both are fired immediately when the input flow "demand" becomes true. In guarded transition systems, it is possible to associate a probability of occurrence to each transition in competition, namely γ to "failureOnDemand" and to "start" in our example.
Eventually, the AltaRica code for the guarded transition system we sketched is given in the Figure hereafter. The motor pump is represented as a "block", i.e. as a container for basic elements. The block declares four variables: a state variable "_state" that takes its value in the domain (set of symbolic constants) "MotorPumpState", and three Boolean flow variables "demand", "in", and "out". Initially, "_state" takes the value "STANDBY". The transfer function is represented by means of the assertion. Assertions tell how to calculate the values of output flow variables from the values of input flow variables and the values of state variables.
domain MotorPumpState {STANDBY, WORKING, FAILED}
block MotorPump
MotorPumpState _state (init = STANDBY);
Boolean demand, in, out (reset = false);
event start (delay = Dirac(0), expectation=gamma);
event failureOnDemand (delay = Dirac(0), expectation=1-gamma);
event stop (delay = Dirac(0));
event failure (delay = exponential(lambda));
event repair (delay = exponential(1/tau));
parameter Real lambda = 1.0e-4;
parameter Real tau = 8;
parameter Real gamma = 0.02;
transition
start: demand and _state==STANDBY -> _state := WORKING;
failureOnDemand: demand and _state==STANDBY -> _state := FAILED;
stop: not demand and _state==WORKING -> _state := STANDBY;
failure: _state==WORKING -> _state := FAILED;
repair: _state==FAILED -> _state := STANDBY;
assertion
out := in and _state==WORKING;
end
The block "MotorPump" declares also five events and as many transitions. Guards of transitions are Boolean conditions on state and flow variables. Actions of transitions modify the values of state variables. Events are associated with delays and possibly expectations (which are used to calculate probabilities of occurrence of transitions in competition). The description of both delays and expectations may involve parameters.
System Structure Modeling Language
In general, systems under study are not made of a single, simple components as the above motor operated pump. Rather, they consists of a network of such components that interact in an organized in a hierarchical way.
To reflect the architecture of the system in the model, one needs dedicated constructs. This is where S2ML (system structure modeling language) comes into the play. S2ML emerged first as the set of structuring constructs for AltaRica 3.0. Then, it has been studied on its own. As of today, S2ML gathers in a coherent way a versatile set of structuring constructs stemmed from object-oriented and prototype-oriented programming.
S2ML consists of height key concepts: the concepts of port, connection, container, prototype, class, cloning, instantiation, inheritance and aggregation.
- Ports
- They are basic modeling elements such as domains, state and flow variables, events and parameters.
- Connections
- They are relations amongst ports such as definitions of domains, probability distributions associated with state variables, definitions of parameters, transitions and assertions.
- Containers
- They gather declarations of ports and connections as well as of other containers forming nested hierarchies. The block describing the motor pump is such a container.
- Prototype and cloning
- Prototypes are individual containers. In AltaRica, blocks are prototypes. When the system under study contains two or more similar parts, it would be both tedious and error prone to duplicate the code. Cloning provides a solution to this problem: the first part is described, then the others are just obtained by cloning the first one. The dot notation makes it possible to access to ports declared in nested blocks, as illustrated by the assertion in the above code.
block System // ... block Line1 // description of line 1 end clones Line1 as Line2; // ... assertion out := Line1.out or Line2.out; end class MotorPump // description of the motor pump. end block System // ... MotorPump P1; // 1st instance MotorPump P2; // 2nd instance // ... end
- Classes and instances
- It is often the case that some modeling components are reused from model to model. It is then possible to create libraries of on-the-shelf modeling components and to instantiate them into model. Classes are used for this purpose. They are just containers (or prototypes) defined outside the model. Instances of classes, also called objects, are clones of these containers defined outside the model.
- Inheritance
- It is the mechanism by which one specializes modeling component. If a derived component D inherits from a base component B, all modeling elements of B are reproduced in D. D may declare additional ports, connections and containers.
- Aggregation
- Cloning and instantiation create components inside components. The inner component is part of the outer one. There are cases however where a component is used by another one, without being part of this component. This mechanism is reflected into model by a mechanism called aggregation. Aggregation is extremely useful to project a functional architecture onto a physical one, and to represent so-called functional chains
AltaRica 3.0 involves a few other constructs, such as a powerful mechanism to synchronize events. The essential has however been presented above.
Adding S2ML on top of a mathematical framework (GTS in the case of AltaRica), makes it possible to pass automatically and at no cost from the model as designed, which reflects the architecture of the system under study, to the model as assessed from which calculations of indicators and simulations can be performed efficiently.
The transformation preserves the semantics of the models and is reversible for the most part: results of calculations and simulations are directly interpretable in the model as designed.
A recent trend in the AltaRica community is the design of modeling patterns. Patterns are pervasive in engineering. They have been developed for instance in the field of technical system architecture, as well as in software engineering. They are useful in reliability engineering also, as they ease design and maintenance of models. They are also a tool for risk analysts to communicate about the models they develop and share.
Tooling and applications
In industrial practice, AltaRica model uses include four main functions:
- Develop a common understanding among stakeholders about how a system works and may fail
- Ensure that the system under study is safe enough to operate
- Optimize maintenance policies
- Assess the average production (or loss of production) of units subject to failure, malfunction, or human error
As these applications require different types of simulations and calculations, several tools have been developed, including:
- Stepwise simulators that interactively play scenarios of evolution
- Compilers that lower level modeling formalisms, primarily fault trees but also Markov chains, to benefit of existing efficient assessment algorithms
- Stochastic simulators that calculate a wide range of risk indicators
- Sequence generators and model-checkers that validate models and extract critical failure scenarios
References
- Signoret, Jean-Pierre (June 1998). "The Altarica Language". ESREL, Proceedings of European Safety and Reliability Association Conference.
- Point, Gérald (1999). "AltaRica: Constraint automata as a description language". Journal Européen des Systèmes Automatisés.
- Arnold, André (2000). "The altarica formalism for describing concurrent systems". Fundamenta Informaticae.
- Point, Gérald (2000). AltaRica: Contribution à l'unification des méthodes formelles et de la sûreté de fonctionnement (Thesis). LaBRI Université Bordeaux I.
- Point, Gérald (2000). AltaRica: Contribution à l'unification des méthodes formelles et de la sûreté de fonctionnement (Thesis). LaBRI Université Bordeaux I.
- Arnold, André (2000). "The altarica formalism for describing concurrent systems". Fundamenta Informaticae.
- Point, Gérald (1999). "AltaRica: Constraint automata as a description language". Journal Européen des Systèmes Automatisés.
- Arnold, André (1994). Finite Transition Systems. Upper Saddle River, New Jersey: C.A.R Hoare. Prentice Hall.
- van Hentenryck, Pascal (1989). Constraint Satisfaction in Logic Programming. Cambridge, MA, USA: The MIT Press.
- Kuntz, Fabien (2011). "Model-based diagnosis for avionics systems using minimal cuts". Proceedings of 22th Worshop on Principles of Diagnosis (DX-2011): 138–145.
- Griffault, Alain (2004). "The mec 5 model-checker". Proceedings of the 16th International Conference on Computed Aided Verification (CAV 2004), Volume 3114 of Lectures Notes in Computer Science: 488–491.
- Griffault, Alain (2004). "Vérification formelle des modèles AltaRica". Hermès, editor, Actes du Congrès de maîrise des risques et de sûreté de fonctionnement, Lambda-Mu'14.
- Vincent, Aymeric (2003). Conception et réalisation d'un vérificateur de modèles AltaRica (Thesis). Université de Bordeaux.
- Boiteau, Marie (2006). "The AltaRica Data-Flow language in use: Assessment of production availability of a multistates system". Reliability Engineering and System Safety. doi:10.1016/j.ress.2004.12.004.
- Rauzy, Antoine (2002). "Modes Automata and their Compilation into Fault Trees". Reliability Engineering and System Safety. 78: 1–12. doi:10.1016/S0951-8320(02)00042-X.
- Bernard, Romain (2008). "Altarica refinement for heterogeneous granularity model analysis". Actes du congrès Lambda-Mu'16.
- Quayzin, Xavier (2009). "Performance modeling of a surveillance mission". Proceedings of the Annual Reliability and Maintainability Symposium.
- Bieber, Pierre (2008). "Integration of formal fault analysis in assert: Case studies and lessons learnt". Proceedings of 4th European Congress Embedded Real Time Software, ERTS 2008.
- Bernard, Romain (2007). "Experiments in model-based safety analysis: flight controls". In Jean-Marc Faure (ed.). Proceedings of IFAC Workshop on Dependable Control of Discrete Systems. pp. 43–48.
- Kombe, Timothy (2011). Modélisation de la propagation des fautes dans les systèmes de production (Thesis). Institut National des Sciences Appliquées de Lyon et École Nationale Supérieure Polytechnique de Yaoundé.
- Adeline, Romain (2011). Méthodes pour la validation de modèles formels pour la Sûreté de Fonctionnement et extension aux problèmes multi-physique (Thesis). Université de Toulouse.
- Bernard, Romain (2009). Analyse de Sécurité multi-systèmes (Thesis). Université de Bordeaux.
- Sagaspe, Laurent (2008). Allocation sûre dans les systèmes aéronautiques : modélisation, vérification et génération (Thesis). Université de Bordeaux.
- Humbert, Sophie (2008). Déclinaison d'exigences de sécurité, du niveau système vers le niveau logiciel, assistée par des modèles formels (Thesis). Université de Bordeaux I.
- Thang Khuu, Minh (2008). Contribution à l'accélération de la simulation stochastique sur des modèles AltaRica Data Flow (Thesis). Université de la Méditerranée (Aix-Marseille II).
- Kehren, Christophe (2005). Motifs formels d'architectures de systèmes pour la sûreté de fonctionnement (Thesis). École Nationale Supérieure de l'Aéronautique et de l'Espace (SUPAERO).
- Pagetti, Claire (2004). Extension temps réel du langage AltaRica (Thesis). École Centrale de Nantes et de l'Université de Nantes.
- Saint-Georges, Benoît; Mailland, David (2023). "Évaluation de la fiabilité en fin de vie d'une constellation de satellites avec AltaRica 3.0". Techniques de l'Ingénieur. doi:10.51257/a-v1-re451.
- Batteux, Michel (2019). "Altarica 3.0 in 10 modeling patterns". International Journal of Critical Computer-Based Systems. doi:10.1504/IJCCBS.2019.098809.
- Batteux, Michel (2017). "AltaRica 3.0: language specification". AltaRica Association.
{{cite web}}: Missing or empty|url=(help) - Rauzy, Antoine (2008). "Guarded transition systems: a new states/events formalism for reliability studies". Journal of Risk and Reliability.
- Batteux, Michel (2017). "Altarica 3.0 assertions: the why and the wherefore". Journal of Risk and Reliability.
- Rauzy, Antoine (2019). "Foundations for model-based systems engineering and model-based safety assessment". Systems Engineering. 22 (2): 146–155. doi:10.1002/sys.21469. S2CID 145040668.
- Batteux, Michel (2018). "From Models of Structures to Structures of Models". 2018 IEEE International Systems Engineering Symposium (ISSE) (PDF). pp. 1–7. doi:10.1109/SysEng.2018.8544424. ISBN 978-1-5386-4446-1. S2CID 54222705.
- Noble, James (1990). Prototype-Based Programming: Concepts, Languages and Applications. Springer-Verlag.
- Abadi, Mauricio (1998). A Theory of Objects. Springer-Verlag.
- Voirin, Jean-Luc (2008). "9.1.1 Method & Tools for constrained System Architecting". INCOSE International Symposium. 18: 775–789. doi:10.1002/j.2334-5837.2008.tb00857.x. S2CID 111113361.
- Batteux, Michel (2019). "Altarica 3.0 in 10 modeling patterns". International Journal of Critical Computer-Based Systems. doi:10.1504/IJCCBS.2019.098809.
- W. Maier, Mark (2009). The Art of Systems Architecting. Boca Raton: CRC Press.
- Gamma, Erich (1994). Design Patterns - Elements of Reusable Object-Oriented Software. Addison-Wesley Professional Computing Series. Addison-Wesley.
 to "start" in our example.
to "start" in our example.