
In condensed matter physics, altermagnetism is a type of persistent magnetic state in ideal crystals. Altermagnetic structures are collinear and crystal-symmetry compensated, resulting in zero net magnetisation. Unlike in an ordinary collinear antiferromagnet, another magnetic state with zero net magnetization, the electronic bands in an altermagnet are not Kramers degenerate, but instead depend on the wavevector in a spin-dependent way. Related to this feature, key experimental observations were published in 2024. It has been speculated that altermagnetism may have applications in the field of spintronics.
Crystal structure and symmetry
In altermagnetic materials, atoms form a regular pattern with alternating spin and spatial orientation at adjacent magnetic sites in the crystal.
Atoms with opposite magnetic moment are in altermagnets coupled by crystal rotation or mirror symmetry. The spatial orientation of magnetic atoms may originate from the surrounding cages of non-magnetic atoms. The opposite spin sublattices in altermagnetic manganese telluride (MnTe) are related by spin rotation combined with six-fold crystal rotation and half-unit cell translation. In altermagnetic ruthenium dioxide (RuO2), the opposite spin sublattices are related by four-fold crystal rotation.

Electronic structure
One of the distinctive features of altermagnets is a specifically spin-split band structure which was first experimentally observed in work that was published in 2024. Altermagnetic band structure breaks time-reversal symmetry, Eks=E-ks (E is energy, k wavevector and s spin) as in ferromagnets, however unlike in ferromagnets, it does not generate net magnetization. The altermagnetic spin polarisation alternates in wavevector space and forms characteristic 2, 4, or 6 spin-degenerate nodes, respectively, which correspond to d-, g, or i-wave order parameters. A d-wave altermagnet can be regarded as the magnetic counterpart of a d-wave superconductor.
-
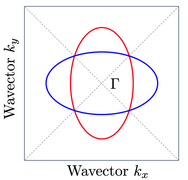 Fermi surface of an altermagnetic metal. The blue and red colors correspond to the up and down polarization of the spin.
Fermi surface of an altermagnetic metal. The blue and red colors correspond to the up and down polarization of the spin.
-
 The band structure of an altermagnet.
The band structure of an altermagnet.
The altermagnetic spin polarization in band structure (energy–wavevector diagram) is collinear and does not break inversion symmetry. The altermagnetic spin splitting is even in wavector, i.e. (kx-ky)sz. It is thus also distinct from noncollinear Rasba or Dresselhaus spin texture which break inversion symmetry in noncentrosymmetric nonmagnetic or antiferromagnetic materials due to the spin-orbit coupling. Unconventional time-reversal symmetry breaking, giant ~1eV spin splitting and anomalous Hall effect was first theoretically predicted and experimentally confirmed in RuO2.
Materials
Direct experimental evidence of altermagnetic band structure in semiconducting MnTe and metallic RuO2 was first published in 2024. Many more materials are predicted to be altermagnets – ranging from insulators, semiconductors, and metals to superconductors. Altermagnetism was predicted in 3D and 2D materials with both light as well as heavy elements and can be found in nonrelativistic as well as relativistic band structures.
Properties
Altermagnets exhibit an unusual combination of ferromagnetic and antiferromagnetic properties, which remarkably more closely resemble those of ferromagnets. Hallmarks of altermagnetic materials such as the anomalous Hall effect have been observed before (but this effect occurs also in other magnetically compensated systems such as non-collinear antiferromagnets). Altermagnets also exhibit unique properties such as anomalous and spin currents that can change sign as the crystal rotates.
References
- ^ Mazin, Igor (2022-12-08). "Altermagnetism—A New Punch Line of Fundamental Magnetism". Physical Review X. 12 (4): 040002. Bibcode:2022PhRvX..12d0002M. doi:10.1103/physrevx.12.040002.
- Mazin, Igor (2024-01-08). "Altermagnetism Then and Now". Physical Review X. 17: 4. arXiv:2105.05820. doi:10.1103/PhysRevX.12.031042.
- ^ Mazin, Igor; González-Hernández, Rafael; Šmejkal, Libor (2023-09-05), Induced Monolayer Altermagnetism in MnP(S,Se)$_3$ and FeSe, arXiv:2309.02355
- Wilkins, Alex (14 February 2024). "The existence of a new kind of magnetism has been confirmed". New Scientist. Retrieved 2024-02-15.
- ^ Savitsky, Zack (2024). "Researchers discover new kind of magnetism". Science. 383 (6683): 574–575. Bibcode:2024Sci...383..574S. doi:10.1126/science.ado5309. PMID 38330121. Retrieved 16 February 2024.
- ^ Šmejkal, Libor; Sinova, Jairo; Jungwirth, Tomas (2022-12-08). "Emerging Research Landscape of Altermagnetism". Physical Review X. 12 (4): 040501. arXiv:2204.10844. Bibcode:2022PhRvX..12d0501S. doi:10.1103/PhysRevX.12.040501.
- ^ Šmejkal, Libor; Sinova, Jairo; Jungwirth, Tomas (2022-09-23). "Altermagnetism: spin-momentum locked phase protected by non-relativistic symmetries". Physical Review X. 12 (3): 031042. arXiv:2105.05820. doi:10.1103/PhysRevX.12.031042. ISSN 2160-3308.
- ^ Krempaský, J.; Šmejkal, L.; D’Souza, S. W.; Hajlaoui, M.; Springholz, G.; Uhlířová, K.; Alarab, F.; Constantinou, P. C.; Strocov, V.; Usanov, D.; Pudelko, W. R.; González-Hernández, R.; Birk Hellenes, A.; Jansa, Z.; Reichlová, H. (February 2024). "Altermagnetic lifting of Kramers spin degeneracy". Nature. 626 (7999): 517–522. arXiv:2308.10681. Bibcode:2024Natur.626..517K. doi:10.1038/s41586-023-06907-7. ISSN 1476-4687. PMC 10866710. PMID 38356066.
- ^ Fedchenko, Olena; Minár, Jan; Akashdeep, Akashdeep; D’Souza, Sunil Wilfred; Vasilyev, Dmitry; Tkach, Olena; Odenbreit, Lukas; Nguyen, Quynh; Kutnyakhov, Dmytro; Wind, Nils; Wenthaus, Lukas; Scholz, Markus; Rossnagel, Kai; Hoesch, Moritz; Aeschlimann, Martin (2024-02-02). "Observation of time-reversal symmetry breaking in the band structure of altermagnetic RuO 2". Science Advances. 10 (5): eadj4883. arXiv:2306.02170. Bibcode:2024SciA...10J4883F. doi:10.1126/sciadv.adj4883. ISSN 2375-2548. PMC 10830110. PMID 38295181.
- Arrell, Miriam (February 14, 2024). "Altermagnetism proves its place on the magnetic family tree". ScienceDaily. Retrieved 2024-02-15.
- ^ Šmejkal, Libor; González-Hernández, Rafael; Jungwirth, T.; Sinova, J. (5 June 2020). "Crystal time-reversal symmetry breaking and spontaneous Hall effect in collinear antiferromagnets". Science Advances. 6 (23): eaaz8809. arXiv:1901.00445. Bibcode:2020SciA....6.8809S. doi:10.1126/sciadv.aaz8809. PMC 7274798. PMID 32548264.
- Šmejkal, Libor; Sinova, Jairo; Jungwirth, Tomas (2022-09-23). "Beyond Conventional Ferromagnetism and Antiferromagnetism: A Phase with Nonrelativistic Spin and Crystal Rotation Symmetry". Physical Review X. 12 (3): 031042. arXiv:2105.05820. Bibcode:2022PhRvX..12c1042S. doi:10.1103/PhysRevX.12.031042.
- ^ Feng, Zexin; Zhou, Xiaorong; Šmejkal, Libor; Wu, Lei; Zhu, Zengwei; Guo, Huixin; González-Hernández, Rafael; Wang, Xiaoning; Yan, Han; Qin, Peixin; Zhang, Xin; Wu, Haojiang; Chen, Hongyu; Meng, Ziang; Liu, Li; Xia, Zhengcai; Sinova, Jairo; Jungwirth, Tomáš; Liu, Zhiqi (7 November 2022). "An anomalous Hall effect in altermagnetic ruthenium dioxide". Nature Electronics. 5 (11): 735–743. arXiv:2002.08712. doi:10.1038/s41928-022-00866-z.
- Gonzalez Betancourt, R. D.; Zubáč, J.; Gonzalez-Hernandez, R.; Geishendorf, K.; Šobáň, Z.; Springholz, G.; Olejník, K.; Šmejkal, L.; Sinova, J.; Jungwirth, T.; Goennenwein, S. T. B.; Thomas, A.; Reichlová, H.; Železný, J.; Kriegner, D. (20 January 2023). "Spontaneous Anomalous Hall Effect Arising from an Unconventional Compensated Magnetic Phase in a Semiconductor". Physical Review Letters. 130 (3): 036702. arXiv:2112.06805. Bibcode:2023PhRvL.130c6702G. doi:10.1103/PhysRevLett.130.036702. PMID 36763381.
- Nakatsuji, Satoru; Kiyohara, Naoki; Higo, Tomoya (November 2015). "Large anomalous Hall effect in a non-collinear antiferromagnet at room temperature". Nature. 527 (7577): 212–215. Bibcode:2015Natur.527..212N. doi:10.1038/nature15723. PMID 26524519.
- González-Hernández, Rafael; Šmejkal, Libor; Výborný, Karel; Yahagi, Yuta; Sinova, Jairo; Jungwirth, Tomáš; Železný, Jakub (2021-03-26). "Efficient Electrical Spin Splitter Based on Nonrelativistic Collinear Antiferromagnetism". Physical Review Letters. 126 (12): 127701. arXiv:2002.07073. Bibcode:2021PhRvL.126l7701G. doi:10.1103/PhysRevLett.126.127701. ISSN 0031-9007. PMID 33834809.
| Magnetism | |
|---|---|
| Magnetic response | |
| Magnetic states | |