In quantum electrodynamics, the anomalous magnetic moment of a particle is a contribution of effects of quantum mechanics, expressed by Feynman diagrams with loops, to the magnetic moment of that particle. The magnetic moment, also called magnetic dipole moment, is a measure of the strength of a magnetic source.
The "Dirac" magnetic moment, corresponding to tree-level Feynman diagrams (which can be thought of as the classical result), can be calculated from the Dirac equation. It is usually expressed in terms of the g-factor; the Dirac equation predicts . For particles such as the electron, this classical result differs from the observed value by a small fraction of a percent. The difference is the anomalous magnetic moment, denoted and defined as
Electron

The one-loop contribution to the anomalous magnetic moment—corresponding to the first and largest quantum mechanical correction—of the electron is found by calculating the vertex function shown in the adjacent diagram. The calculation is relatively straightforward and the one-loop result is: where is the fine-structure constant. This result was first found by Julian Schwinger in 1948 and is engraved on his tombstone. As of 2016, the coefficients of the QED formula for the anomalous magnetic moment of the electron are known analytically up to and have been calculated up to order :
The QED prediction agrees with the experimentally measured value to more than 10 significant figures, making the magnetic moment of the electron one of the most accurately verified predictions in the history of physics. (See Precision tests of QED for details.)
The current experimental value and uncertainty is: According to this value, is known to an accuracy of around 1 part in 10 billion (10). This required measuring to an accuracy of around 1 part in 10 trillion (10).
Muon
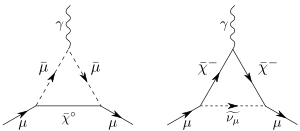
The anomalous magnetic moment of the muon is calculated in a similar way to the electron. The prediction for the value of the muon anomalous magnetic moment includes three parts:
Of the first two components, represents the photon and lepton loops, and the W boson, Higgs boson and Z boson loops; both can be calculated precisely from first principles. The third term, , represents hadron loops; it cannot be calculated accurately from theory alone. It is estimated from experimental measurements of the ratio of hadronic to muonic cross sections (R) in electron–antielectron (
e
–
e
) collisions. As of July 2017, the measurement disagrees with the Standard Model by 3.5 standard deviations, suggesting physics beyond the Standard Model may be having an effect (or that the theoretical/experimental errors are not completely under control). This is one of the long-standing discrepancies between the Standard Model and experiment.
The E821 Experiment at Brookhaven National Laboratory (BNL) studied the precession of muon and antimuon in a constant external magnetic field as they circulated in a confining storage ring. The E821 Experiment reported the following average value
In 2024, the Fermilab collaboration "Muon g−2" doubled the accuracy of this value over the group’s previous measurements from the 2018 data set. The data for the experiment were collected during the 2019–2020 runs. The independent value came in at (0.21 ppm), which, combined with measurements from Brookhaven National Laboratory, yields a world average of (0.19 ppm).
In April 2021, an international group of fourteen physicists reported that by using ab-initio quantum chromodynamics and quantum electrodynamics simulations they were able to obtain a theory-based approximation agreeing more with the experimental value than with the previous theory-based value that relied on the electron–positron annihilation experiments.
Tau
The Standard Model prediction for the tau's anomalous magnetic dipole moment is while the best measured bound for is reported by the CMS experiment at the CERN LHC.
Composite particles
Composite particles often have a huge anomalous magnetic moment. The nucleons, protons and neutrons, both composed of quarks, are examples. The nucleon magnetic moments are both large and were unexpected; the proton's magnetic moment is much too large for an elementary particle, while the neutron's magnetic moment was expected to be zero due to its charge being zero.
See also
References
- Peskin, M. E.; Schroeder, D. V. (1995). "Section 6.3". An Introduction to Quantum Field Theory. Addison-Wesley. ISBN 978-0-201-50397-5.
- Schwinger, J. (1948). "On Quantum-Electrodynamics and the Magnetic Moment of the Electron" (PDF). Physical Review. 73 (4): 416–417. Bibcode:1948PhRv...73..416S. doi:10.1103/PhysRev.73.416.
- Laporta, S.; Remiddi, E. (1996). "The analytical value of the electron (g − 2) at order α in QED". Physics Letters B. 379 (1–4): 283–291. arXiv:hep-ph/9602417. Bibcode:1996PhLB..379..283L. doi:10.1016/0370-2693(96)00439-X.
- Aoyama, T.; Hayakawa, M.; Kinoshita, T.; Nio, M. (2012). "Tenth-Order QED Contribution to the Electron g−2 and an Improved Value of the Fine Structure Constant". Physical Review Letters. 109 (11): 111807. arXiv:1205.5368. Bibcode:2012PhRvL.109k1807A. doi:10.1103/PhysRevLett.109.111807. PMID 23005618. S2CID 14712017.
- Aoyama, Tatsumi; Hayakawa, Masashi; Kinoshita, Toichiro; Nio, Makiko (1 February 2015). "Tenth-Order Electron Anomalous Magnetic Moment – Contribution of Diagrams without Closed Lepton Loops". Physical Review D. 91 (3): 033006. arXiv:1412.8284. Bibcode:2015PhRvD..91c3006A. doi:10.1103/PhysRevD.91.033006. S2CID 119024825.
- Nio, Makiko (3 February 2015). QED tenth-order contribution to the electron anomalous magnetic moment and a new value of the fine-structure constant (PDF). Fundamental Constants Meeting 2015. Eltville, Germany.
- Fan, X.; Myers, T. G.; Sukra, B. A. D.; Gabrielse, G. (13 February 2023). "Measurement of the Electron Magnetic Moment". Physical Review Letters. 130 (7): 071801. arXiv:2209.13084. Bibcode:2023PhRvL.130g1801F. doi:10.1103/PhysRevLett.130.071801. PMID 36867820. S2CID 123962197.
- ^ Patrignani, C.; Agashe, K. (2016). "Review of Particle Physics" (PDF). Chinese Physics C. 40 (10). IOP Publishing: 100001. Bibcode:2016ChPhC..40j0001P. doi:10.1088/1674-1137/40/10/100001. ISSN 1674-1137. S2CID 125766528.
- Giusti, D.; Lubicz, V.; Martinelli, G.; Sanflippo, F.; Simula, S. (2017). "Strange and charm HVP contributions to the muon (g − 2) including QED corrections with twisted-mass fermions". Journal of High Energy Physics. 2017 (10): 157. arXiv:1707.03019. Bibcode:2017JHEP...10..157G. doi:10.1007/JHEP10(2017)157.
- "The E821 Muon (g−2) Home Page". Brookhaven National Laboratory. Retrieved 1 July 2014.
- "Detailed report on the measurement of the positive muon anomalous magnetic moment to 0.20 ppm". Physical Review D. Fermilab. 8 August 2024. Retrieved 16 March 2015.
- Borsany, Szabolcs; et al. (7 April 2021). "Leading hadronic contribution to the muon magnetic moment from lattice QCD". Nature. 593 (7857): 51–55. arXiv:2002.12347. Bibcode:2021Natur.593...51B. doi:10.1038/s41586-021-03418-1. PMID 33828303. S2CID 221151004.
- Eidelman, S.; Passera, M. (30 January 2007). "THEORY OF THE τ LEPTON ANOMALOUS MAGNETIC MOMENT". Modern Physics Letters A. 22 (3): 159–179. arXiv:hep-ph/0701260. Bibcode:2007MPLA...22..159E. doi:10.1142/S0217732307022694. ISSN 0217-7323. S2CID 18000680.
- CMS Collaboration, The (1 October 2024). "Observation of γ γ → τ τ in proton–proton collisions and limits on the anomalous electromagnetic moments of the τ lepton". Reports on Progress in Physics. 87 (10): 107801. arXiv:2406.03975. doi:10.1088/1361-6633/ad6fcb. ISSN 0034-4885.
Bibliography
- Sergei Vonsovsky (1975). Magnetism of Elementary Particles. Mir Publishers.
External links
- Overview of the g−2 experiment
- Kusch, P.; Foley, H. M. (1948). "The Magnetic Moment of the Electron". Physical Review. 74 (3): 250–263. Bibcode:1948PhRv...74..250K. doi:10.1103/PhysRev.74.250.
- Aoyama, T.; et al. (2020). "The anomalous magnetic moment of the muon in the Standard Model". Physics Reports. 887: 1–166. arXiv:2006.04822. Bibcode:2020PhR...887....1A. doi:10.1016/j.physrep.2020.07.006.
| Quantum electrodynamics | |
|---|---|
| Formalism | |
| Particles | |
| Concepts | |
| Processes | |
| See also: | |
 . For particles such as the
. For particles such as the  and defined as
and defined as

 where
where  is the
is the  and have been calculated up to order
and have been calculated up to order  :
:

 According to this value,
According to this value,  is known to an accuracy of around 1 part in 10 billion (10). This required measuring
is known to an accuracy of around 1 part in 10 billion (10). This required measuring 

 represents the photon and lepton loops, and
represents the photon and lepton loops, and  the W boson, Higgs boson and Z boson loops; both can be calculated precisely from first principles. The third term,
the W boson, Higgs boson and Z boson loops; both can be calculated precisely from first principles. The third term,  , represents hadron loops; it cannot be calculated accurately from theory alone. It is estimated from experimental measurements of the ratio of hadronic to muonic cross sections (
, represents hadron loops; it cannot be calculated accurately from theory alone. It is estimated from experimental measurements of the ratio of hadronic to muonic cross sections (
 (0.21 ppm), which, combined with measurements from Brookhaven National Laboratory, yields a world average of
(0.21 ppm), which, combined with measurements from Brookhaven National Laboratory, yields a world average of  (0.19 ppm).
(0.19 ppm).
 while the best measured bound for
while the best measured bound for  is
is
 reported by the CMS experiment at the CERN LHC.
reported by the CMS experiment at the CERN LHC.