Misplaced Pages

In statistics, the Anscombe transform, named after Francis Anscombe, is a variance-stabilizing transformation that transforms a random variable with a Poisson distribution into one with an approximately standard Gaussian distribution. The Anscombe transform is widely used in photon-limited imaging (astronomy, X-ray) where images naturally follow the Poisson law. The Anscombe transform is usually used to pre-process the data in order to make the standard deviation approximately constant. Then denoising algorithms designed for the framework of additive white Gaussian noise are used; the final estimate is then obtained by applying an inverse Anscombe transformation to the denoised data.

Definition

For the Poisson distribution the mean ${\displaystyle m}$ and variance ${\displaystyle v}$ are not independent: ${\displaystyle m=v}$. The Anscombe transform

${\displaystyle A:x\mapsto 2{\sqrt {x+{\tfrac {3}{8}}}}\,}$

aims at transforming the data so that the variance is set approximately 1 for large enough mean; for mean zero, the variance is still zero.

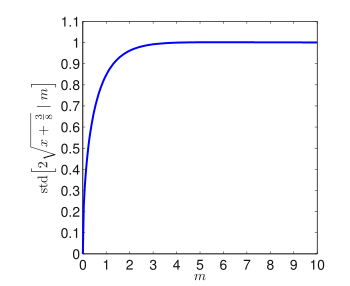
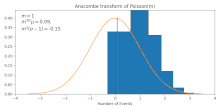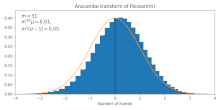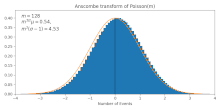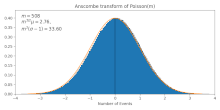
It transforms Poissonian data ${\displaystyle x}$ (with mean ${\displaystyle m}$) to approximately Gaussian data of mean ${\displaystyle 2{\sqrt {m+{\tfrac {3}{8}}}}-{\tfrac {1}{4\,m^{1/2}}}+O\left({\tfrac {1}{m^{3/2}}}\right)}$ and standard deviation ${\displaystyle 1+O\left({\tfrac {1}{m^{2}}}\right)}$. This approximation gets more accurate for larger ${\displaystyle m}$, as can be also seen in the figure.

For a transformed variable of the form ${\displaystyle 2{\sqrt {x+c}}}$, the expression for the variance has an additional term ${\displaystyle {\frac {{\tfrac {3}{8}}-c}{m}}}$; it is reduced to zero at ${\displaystyle c={\tfrac {3}{8}}}$, which is exactly the reason why this value was picked.

Inversion

When the Anscombe transform is used in denoising (i.e. when the goal is to obtain from ${\displaystyle x}$ an estimate of ${\displaystyle m}$), its inverse transform is also needed in order to return the variance-stabilized and denoised data ${\displaystyle y}$ to the original range. Applying the algebraic inverse

${\displaystyle A^{-1}:y\mapsto \left({\frac {y}{2}}\right)^{2}-{\frac {3}{8}}}$

usually introduces undesired bias to the estimate of the mean ${\displaystyle m}$, because the forward square-root transform is not linear. Sometimes using the asymptotically unbiased inverse

${\displaystyle y\mapsto \left({\frac {y}{2}}\right)^{2}-{\frac {1}{8}}}$

mitigates the issue of bias, but this is not the case in photon-limited imaging, for which the exact unbiased inverse given by the implicit mapping

${\displaystyle \operatorname {E} \left=2\sum _{x=0}^{+\infty }\left({\sqrt {x+{\tfrac {3}{8}}}}\cdot {\frac {m^{x}e^{-m}}{x!}}\right)\mapsto m}$

should be used. A closed-form approximation of this exact unbiased inverse is

${\displaystyle y\mapsto {\frac {1}{4}}y^{2}-{\frac {1}{8}}+{\frac {1}{4}}{\sqrt {\frac {3}{2}}}y^{-1}-{\frac {11}{8}}y^{-2}+{\frac {5}{8}}{\sqrt {\frac {3}{2}}}y^{-3}.}$

Alternatives

There are many other possible variance-stabilizing transformations for the Poisson distribution. Bar-Lev and Enis report a family of such transformations which includes the Anscombe transform. Another member of the family is the Freeman-Tukey transformation

${\displaystyle A:x\mapsto {\sqrt {x+1}}+{\sqrt {x}}.\,}$

A simplified transformation, obtained as the primitive of the reciprocal of the standard deviation of the data, is

${\displaystyle A:x\mapsto 2{\sqrt {x}}\,}$

which, while it is not quite so good at stabilizing the variance, has the advantage of being more easily understood. Indeed, from the delta method,

${\displaystyle V\approx \left({\frac {d(2{\sqrt {m}})}{dm}}\right)^{2}V=\left({\frac {1}{\sqrt {m}}}\right)^{2}m=1}$.

Generalization

While the Anscombe transform is appropriate for pure Poisson data, in many applications the data presents also an additive Gaussian component. These cases are treated by a Generalized Anscombe transform and its asymptotically unbiased or exact unbiased inverses.

See also

• Variance-stabilizing transformation
• Box–Cox transformation

References

1. ^ Anscombe, F. J. (1948), "The transformation of Poisson, binomial and negative-binomial data", Biometrika, vol. 35, no. 3–4, , pp. 246–254, doi:10.1093/biomet/35.3-4.246, JSTOR 2332343
2. ^ Bar-Lev, S. K.; Enis, P. (1988), "On the classical choice of variance stabilizing transformations and an application for a Poisson variate", Biometrika, vol. 75, no. 4, pp. 803–804, doi:10.1093/biomet/75.4.803
3. Mäkitalo, M.; Foi, A. (2011), "Optimal inversion of the Anscombe transformation in low-count Poisson image denoising", IEEE Transactions on Image Processing, vol. 20, no. 1, pp. 99–109, Bibcode:2011ITIP...20...99M, CiteSeerX 10.1.1.219.6735, doi:10.1109/TIP.2010.2056693, PMID 20615809, S2CID 10229455
4. Mäkitalo, M.; Foi, A. (2011), "A closed-form approximation of the exact unbiased inverse of the Anscombe variance-stabilizing transformation", IEEE Transactions on Image Processing, vol. 20, no. 9, pp. 2697–2698, Bibcode:2011ITIP...20.2697M, doi:10.1109/TIP.2011.2121085, PMID 21356615, S2CID 7937596
5. Freeman, M. F.; Tukey, J. W. (1950), "Transformations related to the angular and the square root", The Annals of Mathematical Statistics, vol. 21, no. 4, pp. 607–611, doi:10.1214/aoms/1177729756, JSTOR 2236611
6. Starck, J.L.; Murtagh, F.; Bijaoui, A. (1998). Image Processing and Data Analysis. Cambridge University Press. ISBN 9780521599146.
7. Mäkitalo, M.; Foi, A. (2013), "Optimal inversion of the generalized Anscombe transformation for Poisson-Gaussian noise", IEEE Transactions on Image Processing, vol. 22, no. 1, pp. 91–103, Bibcode:2013ITIP...22...91M, doi:10.1109/TIP.2012.2202675, PMID 22692910, S2CID 206724566

Further reading

• Starck, J.-L.; Murtagh, F. (2001), "Astronomical image and signal processing: looking at noise, information and scale", Signal Processing Magazine, IEEE, vol. 18, no. 2, pp. 30–40, Bibcode:2001ISPM...18...30S, doi:10.1109/79.916319, S2CID 13210703

• Poisson distribution
• Normal distribution
• Statistical data transformation