
In quantum physics and quantum chemistry, an avoided crossing (AC, sometimes called intended crossing, non-crossing or anticrossing) is the phenomenon where two eigenvalues of a Hermitian matrix representing a quantum observable and depending on continuous real parameters cannot become equal in value ("cross") except on a manifold of dimension . The phenomenon is also known as the von Neumann–Wigner theorem. In the case of a diatomic molecule (with one parameter, namely the bond length), this means that the eigenvalues cannot cross at all. In the case of a triatomic molecule, this means that the eigenvalues can coincide only at a single point (see conical intersection).
This is particularly important in quantum chemistry. In the Born–Oppenheimer approximation, the electronic molecular Hamiltonian is diagonalized on a set of distinct molecular geometries (the obtained eigenvalues are the values of the adiabatic potential energy surfaces). The geometries for which the potential energy surfaces are avoiding to cross are the locus where the Born–Oppenheimer approximation fails.
Avoided crossing also occur in the resonance frequencies of undamped mechanical systems, where the stiffness and mass matrices are real symmetric. There the resonance frequencies are the square root of the generalized eigenvalues.
In two-state systems
Emergence
Study of a two-level system is of vital importance in quantum mechanics because it embodies simplification of many of physically realizable systems. The effect of perturbation on a two-state system Hamiltonian is manifested through avoided crossings in the plot of individual energy versus energy difference curve of the eigenstates. The two-state Hamiltonian can be written as
The eigenvalues of which are and and the eigenvectors, and . These two eigenvectors designate the two states of the system. If the system is prepared in either of the states it would remain in that state. If happens to be equal to there will be a twofold degeneracy in the Hamiltonian. In that case any superposition of the degenerate eigenstates is evidently another eigenstate of the Hamiltonian. Hence the system prepared in any state will remain in that forever.
However, when subjected to an external perturbation, the matrix elements of the Hamiltonian change. For the sake of simplicity we consider a perturbation with only off diagonal elements. Since the overall Hamiltonian must be Hermitian we may simply write the new Hamiltonian
Where P is the perturbation with zero diagonal terms. The fact that P is Hermitian fixes its off-diagonal components. The modified eigenstates can be found by diagonalising the modified Hamiltonian. It turns out that the new eigenvalues and are
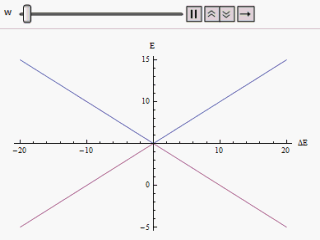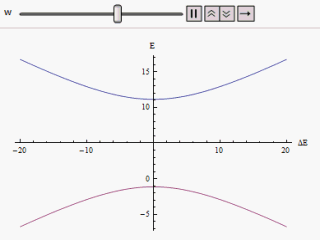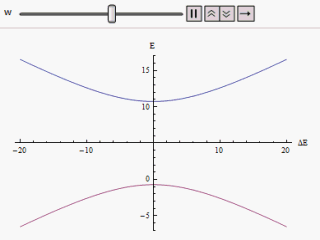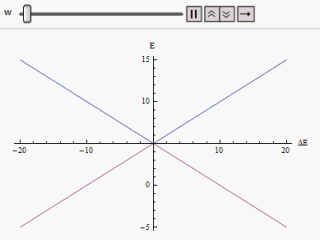
If a graph is plotted varying along the horizontal axis and or along the vertical, we find two branches of a hyperbola (as shown in the figure). The curve asymptotically approaches the original unperturbed energy levels. Analyzing the curves it becomes evident that even if the original states were degenerate (i.e. ) the new energy states are no longer equal. However, if is set to zero we may find at , and the levels cross. Thus with the effect of the perturbation these level crossings are avoided.
Quantum resonance
The immediate impact of avoided level crossing in a degenerate two state system is the emergence of a lowered energy eigenstate. The effective lowering of energy always correspond to increasing stability.(see: Energy minimization) Bond resonance in organic molecules exemplifies the occurrence of such avoided crossings. To describe these cases we may note that the non-diagonal elements in an erstwhile diagonalised Hamiltonian not only modify the energy eigenvalues but also superpose the old eigenstates into the new ones. These effects are more prominent if the original Hamiltonian had degeneracy. This superposition of eigenstates to attain more stability is precisely the phenomena of chemical bond resonance.
Our earlier treatment started by denoting the eigenvectors and as the matrix representation of eigenstates and of a two-state system. Using bra–ket notation the matrix elements of are actually the terms
- with
where due to the degeneracy of the unperturbed Hamiltonian and the off-diagonal perturbations are and .
The new eigenstates and can be found by solving the eigenvalue equations and . From simple calculations it can be shown that
- and
- where
It is evident that both of the new eigenstates are superposition of the original degenerate eigenstates and one of the eigenvalues (here ) is less than the original unperturbed eigenenergy. So the corresponding stable system will naturally mix up the former unperturbed eigenstates to minimize its energy. In the example of benzene the experimental evidences of probable bond structures give rise to two different eigenstates, and . The symmetry of these two structures mandates that .
However it turns out that the two-state Hamiltonian of benzene is not diagonal. The off-diagonal elements result into lowering of energy and the benzene molecule stabilizes in a structure which is a superposition of these symmetric ones with energy . For any general two-state system avoided level crossing repels the eigenstates and such that it requires more energy for the system to achieve the higher energy configuration.
Resonances in avoided crossing
In molecules, the nonadiabatic couplings between two adiabatic potentials build the AC region. Because they are not in the bound state region of the adiabatic potentials, the rovibronic resonances in the AC region of two-coupled potentials are very special and usually do not play important roles on the scatterings. Exemplified in particle scattering, resonances in the AC region are comprehensively investigated. The effects of resonances in the AC region on the scattering cross sections strongly depend on the nonadiabatic couplings of the system, it can be very significant as sharp peaks, or inconspicuous buried in the background. More importantly, it shows a simple quantity proposed by Zhu and Nakamura to classify the coupling strength of nonadiabatic interactions, can be well applied to quantitatively estimate the importance of resonances in the AC region.
General avoided crossing theorem
The above illustration of avoided crossing however is a very specific case. From a generalised view point the phenomenon of avoided crossing is actually controlled by the parameters behind the perturbation. For the most general perturbation affecting a two-dimensional subspace of the Hamiltonian , we may write the effective Hamiltonian matrix in that subspace as
Here the elements of the state vectors were chosen to be real so that all the matrix elements become real. Now the eigenvalues of the system for this subspace are given by
The terms under the square root are squared real numbers. So for these two levels to cross we simultaneously require
Now if the perturbation has parameters we may in general vary these numbers to satisfy these two equations.
If we choose the values of to then both of the equations above have one single free parameter. In general it is not possible to find one such that both of the equations are satisfied. However, if we allow another parameter to be free, both of these two equations will now be controlled by the same two parameters
And generally there will be two such values of them for which the equations will be simultaneously satisfied. So with distinct parameters parameters can always be chosen arbitrarily and still we can find two such s such that there would be crossing of energy eigenvalues. In other words, the values of and would be the same for freely varying co-ordinates (while the rest of the two co-ordinates are fixed from the condition equations). Geometrically the eigenvalue equations describe a surface in dimensional space.
Since their intersection is parametrized by coordinates, we may formally state that for continuous real parameters controlling the perturbed Hamiltonian, the levels (or surfaces) can only cross at a manifold of dimension . However the symmetry of the Hamiltonian has a role to play in the dimensionality. If the original Hamiltonian has asymmetric states, , the off-diagonal terms vanish automatically to ensure hermiticity. This allows us to get rid of the equation . Now from similar arguments as posed above, it is straightforward that for an asymmetrical Hamiltonian, the intersection of energy surfaces takes place in a manifold of dimension .
In polyatomic molecules
In an N-atomic polyatomic molecule there are 3N-6 vibrational coordinates (3N-5 for a linear molecule) that enter into the electronic Hamiltonian as parameters. For a diatomic molecule there is only one such coordinate, the bond length r. Thus, due to the avoided crossing theorem, in a diatomic molecule we cannot have level crossings between electronic states of the same symmetry. However, for a polyatomic molecule there is more than one geometry parameter in the electronic Hamiltonian and level crossings between electronic states of the same symmetry are not avoided.
See also
- Geometric phase
- Christopher Longuet-Higgins
- Conical intersection
- Vibronic coupling
- Adiabatic theorem
- Bond hardening
- Bond softening
- Landau–Zener formula
- Level repulsion
References
- Verhoeven 1996, pp. 2229, 2248.
- ^ Landau & Lifshitz 1965, p. 282.
- Cohen-Tannoudji, Diu & Laloë 1992, p. 409.
- Cohen-Tannoudji, Diu & Laloë 1992, p. 410.
- Cohen-Tannoudji, Diu & Laloë 1992, p. 411.
- Yang et. al. 2020, p. 1.
- Landau & Lifshitz 1965, p. 280.
- von Neumann, J.; Wigner, E.P. (1993). "Über merkwürdige diskrete Eigenwerte". The Collected Works of Eugene Paul Wigner (in German). Vol. 30. pp. 465–467. doi:10.1007/978-3-662-02781-3_19. ISBN 978-3-642-08154-5 – via The Collected Works of Eugene Paul Wigner.
{{cite book}}:|journal=ignored (help) - Longuet-Higgins, H. C. (24 June 1975). "The Intersection of Potential Energy Surfaces in Polyatomic Molecules". Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences. 344 (1637). The Royal Society: 147–156. Bibcode:1975RSPSA.344..147L. doi:10.1098/rspa.1975.0095. ISSN 1364-5021. S2CID 98014536.
Sources
- Verhoeven, J. W. (1996-01-01). "Glossary of terms used in photochemistry (IUPAC Recommendations 1996)". Pure and Applied Chemistry. 68 (12): 2223–2286. doi:10.1351/pac199668122223.
- Landau, Lev D.; Lifshitz, Evgeny M. (1965). Quantum Mechanics: Non-relativistic Theory. Vol. 3 (2nd ed.). Pergamon Press.
- Cohen-Tannoudji, Claude; Diu, Bernard; Laloë, Franck (1992). Quantum Mechanics. Vol. 1. New York, NY: Wiley. ISBN 9780471569527.
- Yang, Yu Kun; Cheng, Yongjun; Wu, Yong; Qu, Yi Zhi; Wang, Jian Guo; Zhang, Song Bin (2020-12-01). "Particle scattering and resonances involving avoided crossing". New Journal of Physics. 22 (12). 123022. doi:10.1088/1367-2630/abcfed.
 continuous real parameters cannot become equal in value ("cross") except on a
continuous real parameters cannot become equal in value ("cross") except on a  . The phenomenon is also known as the von Neumann–Wigner theorem. In the case of a
. The phenomenon is also known as the von Neumann–Wigner theorem. In the case of a 
 and
and  and the
and the  and
and  . These two eigenvectors designate the two states of the system. If the system is prepared in either of the states it would remain in that state. If
. These two eigenvectors designate the two states of the system. If the system is prepared in either of the states it would remain in that state. If  there will be a twofold
there will be a twofold  . In the absence of external perturbation the levels would have crossed if the original energy states were degenerate, i.e.
. In the absence of external perturbation the levels would have crossed if the original energy states were degenerate, i.e. 

 and
and  are
are

 along the horizontal axis and
along the horizontal axis and  ) the new energy states are no longer equal. However, if
) the new energy states are no longer equal. However, if  is set to zero we may find at
is set to zero we may find at  ,
,  and the levels cross. Thus with the effect of the perturbation these level crossings are avoided.
and the levels cross. Thus with the effect of the perturbation these level crossings are avoided.
 and
and  of a two-state system. Using
of a two-state system. Using  are actually the terms
are actually the terms
 with
with 
 due to the degeneracy of the unperturbed Hamiltonian and the off-diagonal perturbations are
due to the degeneracy of the unperturbed Hamiltonian and the off-diagonal perturbations are  and
and  .
.
 and
and  can be found by solving the eigenvalue equations
can be found by solving the eigenvalue equations  and
and  . From simple calculations it can be shown that
. From simple calculations it can be shown that
 and
and where
where 
 ) is less than the original unperturbed eigenenergy. So the corresponding stable system will naturally mix up the former unperturbed eigenstates to minimize its energy. In the example of
) is less than the original unperturbed eigenenergy. So the corresponding stable system will naturally mix up the former unperturbed eigenstates to minimize its energy. In the example of  .
.

 of benzene is not diagonal. The off-diagonal elements result into lowering of energy and the benzene molecule stabilizes in a structure which is a superposition of these symmetric ones with energy
of benzene is not diagonal. The off-diagonal elements result into lowering of energy and the benzene molecule stabilizes in a structure which is a superposition of these symmetric ones with energy  . For any general two-state system avoided level crossing repels the eigenstates
. For any general two-state system avoided level crossing repels the eigenstates  and
and  such that it requires more energy for the system to achieve the higher energy configuration.
such that it requires more energy for the system to achieve the higher energy configuration.
 affecting a two-dimensional
affecting a two-dimensional 



 has
has  we may in general vary these numbers to satisfy these two equations.
we may in general vary these numbers to satisfy these two equations.


 to
to  then both of the equations above have one single free parameter. In general it is not possible to find one
then both of the equations above have one single free parameter. In general it is not possible to find one  such that both of the equations are satisfied. However, if we allow another parameter to be free, both of these two equations will now be controlled by the same two parameters
such that both of the equations are satisfied. However, if we allow another parameter to be free, both of these two equations will now be controlled by the same two parameters


 and
and 
 , the off-diagonal terms vanish automatically to ensure hermiticity. This allows us to get rid of the equation
, the off-diagonal terms vanish automatically to ensure hermiticity. This allows us to get rid of the equation  . Now from similar arguments as posed above, it is straightforward that for an asymmetrical Hamiltonian, the intersection of energy surfaces takes place in a manifold of dimension
. Now from similar arguments as posed above, it is straightforward that for an asymmetrical Hamiltonian, the intersection of energy surfaces takes place in a manifold of dimension  .
.