
In particle physics, proton decay is a hypothetical form of particle decay in which the proton decays into lighter subatomic particles, such as a neutral pion and a positron. The proton decay hypothesis was first formulated by Andrei Sakharov in 1967. Despite significant experimental effort, proton decay has never been observed. If it does decay via a positron, the proton's half-life is constrained to be at least 1.67×10 years.
According to the Standard Model, the proton, a type of baryon, is stable because baryon number (quark number) is conserved (under normal circumstances; see Chiral anomaly for an exception). Therefore, protons will not decay into other particles on their own, because they are the lightest (and therefore least energetic) baryon. Positron emission and electron capture—forms of radioactive decay in which a proton becomes a neutron—are not proton decay, since the proton interacts with other particles within the atom.
Some beyond-the-Standard-Model grand unified theories (GUTs) explicitly break the baryon number symmetry, allowing protons to decay via the Higgs particle, magnetic monopoles, or new X bosons with a half-life of 10 to 10 years. For comparison, the universe is roughly 1.38×10 years old. To date, all attempts to observe new phenomena predicted by GUTs (like proton decay or the existence of magnetic monopoles) have failed.
Quantum tunnelling may be one of the mechanisms of proton decay.
Quantum gravity (via virtual black holes and Hawking radiation) may also provide a venue of proton decay at magnitudes or lifetimes well beyond the GUT scale decay range above, as well as extra dimensions in supersymmetry.
There are theoretical methods of baryon violation other than proton decay including interactions with changes of baryon and/or lepton number other than 1 (as required in proton decay). These included B and/or L violations of 2, 3, or other numbers, or B − L violation. Such examples include neutron oscillations and the electroweak sphaleron anomaly at high energies and temperatures that can result between the collision of protons into antileptons or vice versa (a key factor in leptogenesis and non-GUT baryogenesis).
Baryogenesis
Main article: Baryogenesis Unsolved problem in physics: Do protons decay? If so, then what is the half-life? Can nuclear binding energy affect this? (more unsolved problems in physics)One of the outstanding problems in modern physics is the predominance of matter over antimatter in the universe. The universe, as a whole, seems to have a nonzero positive baryon number density – that is, there is more matter than antimatter. Since it is assumed in cosmology that the particles we see were created using the same physics we measure today, it would normally be expected that the overall baryon number should be zero, as matter and antimatter should have been created in equal amounts. This has led to a number of proposed mechanisms for symmetry breaking that favour the creation of normal matter (as opposed to antimatter) under certain conditions. This imbalance would have been exceptionally small, on the order of 1 in every 10 particles a small fraction of a second after the Big Bang, but after most of the matter and antimatter annihilated, what was left over was all the baryonic matter in the current universe, along with a much greater number of bosons.
Most grand unified theories explicitly break the baryon number symmetry, which would account for this discrepancy, typically invoking reactions mediated by very massive X bosons (
X
) or massive Higgs bosons (
H
). The rate at which these events occur is governed largely by the mass of the intermediate
X
or
H
particles, so by assuming these reactions are responsible for the majority of the baryon number seen today, a maximum mass can be calculated above which the rate would be too slow to explain the presence of matter today. These estimates predict that a large volume of material will occasionally exhibit a spontaneous proton decay.
Experimental evidence
Proton decay is one of the key predictions of the various grand unified theories (GUTs) proposed in the 1970s, another major one being the existence of magnetic monopoles. Both concepts have been the focus of major experimental physics efforts since the early 1980s. To date, all attempts to observe these events have failed; however, these experiments have been able to establish lower bounds on the half-life of the proton. Currently, the most precise results come from the Super-Kamiokande water Cherenkov radiation detector in Japan: a lower bound on the proton's half-life of 2.4×10 years via positron decay, and similarly, 1.6×10 years via antimuon decay, close to a supersymmetry (SUSY) prediction of 10–10 years. An upgraded version, Hyper-Kamiokande, probably will have sensitivity 5–10 times better than Super-Kamiokande.
Theoretical motivation
Despite the lack of observational evidence for proton decay, some grand unification theories, such as the SU(5) Georgi–Glashow model and SO(10), along with their supersymmetric variants, require it. According to such theories, the proton has a half-life of about 10~10 years and decays into a positron and a neutral pion that itself immediately decays into two gamma ray photons:
Since a positron is an antilepton this decay preserves B − L number, which is conserved in most GUTs.
Additional decay modes are available (e.g.:
p
→
μ
+
π
), both directly and when catalyzed via interaction with GUT-predicted magnetic monopoles. Though this process has not been observed experimentally, it is within the realm of experimental testability for future planned very large-scale detectors on the megaton scale. Such detectors include the Hyper-Kamiokande.
Early grand unification theories (GUTs) such as the Georgi–Glashow model, which were the first consistent theories to suggest proton decay, postulated that the proton's half-life would be at least 10 years. As further experiments and calculations were performed in the 1990s, it became clear that the proton half-life could not lie below 10 years. Many books from that period refer to this figure for the possible decay time for baryonic matter. More recent findings have pushed the minimum proton half-life to at least 10–10 years, ruling out the simpler GUTs (including minimal SU(5) / Georgi–Glashow) and most non-SUSY models. The maximum upper limit on proton lifetime (if unstable), is calculated at 6×10 years, a bound applicable to SUSY models, with a maximum for (minimal) non-SUSY GUTs at 1.4×10 years.
Although the phenomenon is referred to as "proton decay", the effect would also be seen in neutrons bound inside atomic nuclei. Free neutrons—those not inside an atomic nucleus—are already known to decay into protons (and an electron and an antineutrino) in a process called beta decay. Free neutrons have a half-life of 10 minutes (610.2±0.8 s) due to the weak interaction. Neutrons bound inside a nucleus have an immensely longer half-life – apparently as great as that of the proton.
Projected proton lifetimes
| Theory class | Proton lifetime (years) | Ruled out experimentally? |
|---|---|---|
| Minimal SU(5) (Georgi–Glashow) | 10–10 | Yes |
| Minimal SUSY SU(5) | 10–10 | Yes |
| SUGRA SU(5) | 10–10 | Yes |
| SUSY SO(10) | 10–10 | Partially |
| SUSY SU(5) (MSSM) | ~10 | Partially |
| SUSY SU(5) – 5 dimensions | 10–10 | Partially |
| SUSY SO(10) MSSM G(224) | 2×10 | No |
| Minimal (Basic) SO(10) – Non-SUSY | < ~10 (maximum range) | No |
| Flipped SU(5) (MSSM) | 10–10 | No |
The lifetime of the proton in vanilla SU(5) can be naively estimated as . Supersymmetric GUTs with reunification scales around µ ~ 2×10 GeV/c yield a lifetime of around 10 yr, roughly the current experimental lower bound.
Decay operators
Dimension-6 proton decay operators
The dimension-6 proton decay operators are and where is the cutoff scale for the Standard Model. All of these operators violate both baryon number (B) and lepton number (L) conservation but not the combination B − L.
In GUT models, the exchange of an X or Y boson with the mass ΛGUT can lead to the last two operators suppressed by . The exchange of a triplet Higgs with mass M can lead to all of the operators suppressed by . See Doublet–triplet splitting problem.
- Proton decay. These graphics refer to the X bosons and Higgs bosons.
-
 Dimension-6 proton decay mediated by the X boson (3,2)
Dimension-6 proton decay mediated by the X boson (3,2)
−5⁄6 in SU(5) GUT -
 Dimension-6 proton decay mediated by the
Dimension-6 proton decay mediated by the
X boson (3,2)
1⁄6 in flipped SU(5) GUT -
 Dimension-6 proton decay mediated by the
Dimension-6 proton decay mediated by the
triplet Higgs T (3,1)
−1⁄3 and the
anti-triplet Higgs T (3,1)
1⁄3 in SU(5) GUT
Dimension-5 proton decay operators
In supersymmetric extensions (such as the MSSM), we can also have dimension-5 operators involving two fermions and two sfermions caused by the exchange of a tripletino of mass M. The sfermions will then exchange a gaugino or Higgsino or gravitino leaving two fermions. The overall Feynman diagram has a loop (and other complications due to strong interaction physics). This decay rate is suppressed by where MSUSY is the mass scale of the superpartners.
Dimension-4 proton decay operators
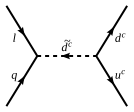
In the absence of matter parity, supersymmetric extensions of the Standard Model can give rise to the last operator suppressed by the inverse square of sdown quark mass. This is due to the dimension-4 operators
q
ℓ
d͂
and
u
d
d͂
.
The proton decay rate is only suppressed by which is far too fast unless the couplings are very small.
See also
References
- Ahmad, Ishfaq (1969), "Radioactive decays by Protons. Myth or reality?", The Nucleus, pp. 69–70
- Bajc, Borut; Hisano, Junji; Kuwahara, Takumi; Omura, Yuji (2016). "Threshold corrections to dimension-six proton decay operators in non-minimal SUSY SU(5) GUTs". Nuclear Physics B. 910: 1. arXiv:1603.03568. Bibcode:2016NuPhB.910....1B. doi:10.1016/j.nuclphysb.2016.06.017. S2CID 119212168.
- Francis, Matthew R. (22 September 2015). "Do protons decay?". symmetry magazine. Retrieved 2020-11-12.
- Talou, P.; Carjan, N.; Strottman, D. (1998). "Time-dependent properties of proton decay from crossing single-particle metastable states in deformed nuclei". Physical Review C. 58 (6): 3280–3285. arXiv:nucl-th/9809006. Bibcode:1998PhRvC..58.3280T. doi:10.1103/PhysRevC.58.3280. S2CID 119075457.
- Dicus, D. A.; Letaw, J. R.; Teplitz, D. C.; Teplitz, V. L. (January 1982). "Effects of proton decay on the cosmological future". The Astrophysical Journal. 252: 1. Bibcode:1982ApJ...252....1D. doi:10.1086/159528. ISSN 0004-637X.
- Trixler, F. (2013). "Quantum Tunnelling to the Origin and Evolution of Life". Current Organic Chemistry. 17 (16): 1758–1770. doi:10.2174/13852728113179990083. PMC 3768233. PMID 24039543.
- Bambi, Cosimo; Freese, Katherine (2008). "Dangerous implications of a minimum length in quantum gravity". Classical and Quantum Gravity. 25 (19): 195013. arXiv:0803.0749. Bibcode:2008CQGra..25s5013B. doi:10.1088/0264-9381/25/19/195013. hdl:2027.42/64158. S2CID 2040645.
- Adams, Fred C.; Kane, Gordon L.; Mbonye, Manasse; Perry, Malcolm J. (2001). "Proton Decay, Black Holes, and Large Extra Dimensions - NASA/ADS". International Journal of Modern Physics A. 16 (13): 2399–2410. arXiv:hep-ph/0009154. Bibcode:2001IJMPA..16.2399A. doi:10.1142/S0217751X0100369X. S2CID 14989175.
- Al-Modlej, Abeer; Alsaleh, Salwa; Alshal, Hassan; Ali, Ahmed Farag (2019). "Proton decay and the quantum structure of space–time". Canadian Journal of Physics. 97 (12): 1317–1322. arXiv:1903.02940. Bibcode:2019CaJPh..97.1317A. doi:10.1139/cjp-2018-0423. hdl:1807/96892. S2CID 119507878.
- Giddings, Steven B. (1995). "The black hole information paradox". arXiv:hep-th/9508151.
- Alsaleh, Salwa; Al-Modlej, Abeer; Farag Ali, Ahmed (2017). "Virtual black holes from the generalized uncertainty principle and proton decay". Europhysics Letters. 118 (5): 50008. arXiv:1703.10038. Bibcode:2017EL....11850008A. doi:10.1209/0295-5075/118/50008. S2CID 119369813.
- Tye, S.-H. Henry; Wong, Sam S. C. (2015). "Bloch wave function for the periodic sphaleron potential and unsuppressed baryon and lepton number violating processes". Physical Review D. 92 (4): 045005. arXiv:1505.03690. Bibcode:2015PhRvD..92d5005T. doi:10.1103/PhysRevD.92.045005. S2CID 73528684.
- Mine, Shunichi (2023). "Nucleon decay: theory and experimental overview". Zenodo. doi:10.5281/zenodo.10493165.
- "Proton lifetime is longer than 10 years". Kamioka Observatory. 25 November 2009. Archived from the original on 16 July 2011.
- Sreekantan, B.V. (1984). "Searches for proton decay and superheavy magnetic monopoles" (PDF). Journal of Astrophysics and Astronomy. 5 (3): 251–271. Bibcode:1984JApA....5..251S. doi:10.1007/BF02714542. S2CID 53964771.
- ^ Nath, Pran; Fileviez Pérez, Pavel (2007). "Proton stability in grand unified theories, in strings and in branes". Physics Reports. 441 (5–6): 191–317. arXiv:hep-ph/0601023. Bibcode:2007PhR...441..191N. doi:10.1016/j.physrep.2007.02.010. S2CID 119542637.
- Olive, K. A.; et al. (Particle Data Group) (2014). "Review of Particle Physics – N Baryons" (PDF). Chinese Physics C. 38 (9): 090001. arXiv:astro-ph/0601168. Bibcode:2014ChPhC..38i0001O. doi:10.1088/1674-1137/38/9/090001. S2CID 118395784.
- Bueno, Antonio; Melgarejo, Antonio J; Navas, Sergio; Dai, Zuxiang; Ge, Yuanyuan; Laffranchi, Marco; Meregaglia, Anselmo; Rubbia, André (2007-04-11). "Nucleon decay searches with large liquid Argon TPC detectors at shallow depths: atmospheric neutrinos and cosmogenic backgrounds". Journal of High Energy Physics. 2007 (4): 041. arXiv:hep-ph/0701101. Bibcode:2007JHEP...04..041B. doi:10.1088/1126-6708/2007/04/041. ISSN 1029-8479. S2CID 119426496.
- Chanowitz, Michael S.; Ellis, John; Gaillard, Mary K. (3 October 1977). "The price of natural flavour conservation in neutral weak interactions". Nuclear Physics B. 128 (3): 506–536. Bibcode:1977NuPhB.128..506C. doi:10.1016/0550-3213(77)90057-8. ISSN 0550-3213. S2CID 121007369.
Further reading
- Amsler, C.; et al. (Particle Data Group) (September 2008). "Review of Particle Physics – N Baryons" (PDF). Physics Letters B. 667 (1–5): 1–6. Bibcode:2008PhLB..667....1A. doi:10.1016/j.physletb.2008.07.018. hdl:1854/LU-685594. S2CID 227119789.
- Hagiwara, K.; et al. (Particle Data Group) (July 2002). "Review of Particle Physics – N Baryons" (PDF). Physical Review D. 66 (1): 010001. Bibcode:2002PhRvD..66a0001H. doi:10.1103/PhysRevD.66.010001. ISSN 0556-2821.
- Adams, Fred; Laughlin, Greg (2000). The five ages of the universe: inside the physics of eternity. London: Touchstone Books. ISBN 978-0-684-86576-8.
- Krauss, Lawrence Maxwell (2001). Atom: an odyssey from the big bang to life on earth-- and beyond. Boston: Little Brown & Company. ISBN 978-0-316-49946-0.
- Wu, Dan-di; Li, Tie-zhong (1985). "Proton decay, annihilation or fusion?". Zeitschrift für Physik. 27 (2): 321–323. Bibcode:1985ZPhyC..27..321W. doi:10.1007/BF01556623. ISSN 0170-9739. S2CID 121868029.
- Nath, Pran; Fileviez Pérez, Pavel (April 2007). "Proton stability in grand unified theories, in strings and in branes". Physics Reports. 441 (5–6): 191–317. arXiv:hep-ph/0601023. Bibcode:2007PhR...441..191N. doi:10.1016/j.physrep.2007.02.010. S2CID 119542637.
External links
- Proton decay at Super-Kamiokande
- Pictorial history of the IMB experiment
- Luciano Maiani (8 February 2006). The problem of proton decay (PDF). Third NO-VE International Workshop on Neutrino Oscillations in Venice. Venice.
| Proton decay experiments | |
|---|---|
| Operating | |
| Retired | |
| Proposed | |
| See also | |

 . Supersymmetric GUTs with reunification scales around µ ~ 2×10
. Supersymmetric GUTs with reunification scales around µ ~ 2×10 

 and
and  where
where  is the
is the  . The exchange of a triplet Higgs with mass M can lead to all of the operators suppressed by
. The exchange of a triplet Higgs with mass M can lead to all of the operators suppressed by  . See
. See  where MSUSY is the mass scale of the
where MSUSY is the mass scale of the  which is far too fast unless the couplings are very small.
which is far too fast unless the couplings are very small.