Blade solidity is an important design parameter for the axial flow impeller and is defined as the ratio of blade chord length to spacing.
- Blade Solidity = c/s
Where
- is the spacing
- is the mean radius
- is blade number
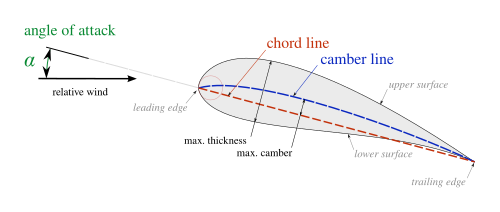
- Chord length c is the length of the chord line
In case of an axial flow impeller, the mean radius is defined in terms of hub (,inner radius) and tip radius (,outer radius) as :
Blade solidity affects various turbomachinery parameters, so to vary those parameters, one needs to vary blade solidity. However, there are some limitations imposed by aspect ratio (span/chord) and pitch. If an impeller has only a few blades (i.e a large pitch), it will result in less lift force and in a similar manner for more blades (i.e. very low pitch), there will be high drag force.
Blade solidity should not be confused with rotor solidity, which is the ratio of the total area of the rotor blades to the swept area of the rotor.
Flow over isolated airfoil
Blade solidity is an important parameter that inter relates turbomachine parameters to airfoil parameters. Lift and drag coefficient for an airfoil is inter related to blade solidity as shown:
where:
- is lift coefficient
- is the drag coefficient
- is the inlet flow angle on the airfoil
- is the outlet flow angle on the airfoil
- is the mean flow angle
- is inlet flow velocity i.e relative to airfoil
- is mean flow velocity
- is the pressure loss
In an airfoil, the mean line curvature is designed to change the flow direction, the vane thickness is for strength and the streamlined shape is to delay the onset of boundary layer separation. Taking all the design factors of an airfoil, the resulting forces of lift and drag can be expressed in terms of lift and drag coefficient.
- where:
- b is the wingspan, and
- c is the chord length
Preliminary design procedure
The design of the impeller depends on specific speed, hub-tip ratio and solidity ratio. To illustrate the dependence, an expression for axial flow pump and fan is shown:
where:
- is ratio of hub to tip diameter
- is the specific speed
Cordier diagram can be used to determine specific speed and impeller tip diameter . Accordingly solidity ratio and hub-tip ratio (range 0.3-0.7) can be adjusted.
Solidity ratio generally falls in the range of 0.4-1.1
See also
References
| This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this article by introducing more precise citations. (March 2017) (Learn how and when to remove this message) |
- Peng, William W. (2008), Fundamentals of Turbomachinery, Wiley, ISBN 978-0-470-12422-2
- Venkanna, B.K. (2009), Fundamentals of Turbomachinery, PHI learning private limited, ISBN 978-81-203-3775-6
- Turton, R.K. (1995), Principles of turbomachinery, Springer (New Delhi), ISBN 8184896042
- Rama, S.R. Gorla (2003), Turbomachinery Design and Theory, Marcel Dekker, Inc., ISBN 0-8247-0980-2
- Yahya, S.M. (2002), Turbines, compressors and fans, TMH, ISBN 0070707022
 is the spacing
is the spacing is the mean radius
is the mean radius is blade number
is blade number ,inner radius) and tip radius (
,inner radius) and tip radius ( ,outer radius) as :
,outer radius) as :



 is
is  is the
is the  is the inlet flow angle on the airfoil
is the inlet flow angle on the airfoil is the outlet flow angle on the airfoil
is the outlet flow angle on the airfoil is the mean flow angle
is the mean flow angle is inlet flow velocity i.e relative to airfoil
is inlet flow velocity i.e relative to airfoil is mean flow velocity
is mean flow velocity is the pressure loss
is the pressure loss



 is ratio of hub to tip diameter
is ratio of hub to tip diameter is the specific speed
is the specific speed . Accordingly solidity ratio and hub-tip ratio (range 0.3-0.7) can be adjusted.
. Accordingly solidity ratio and hub-tip ratio (range 0.3-0.7) can be adjusted.