| Part of a series of articles about |
| Quantum mechanics |
|---|
| Schrödinger equation |
| Background |
| Fundamentals |
| Experiments |
| Formulations |
| Equations |
| Interpretations |
| Advanced topics |
Scientists
|



The Bohr–Sommerfeld model (also known as the Sommerfeld model or Bohr–Sommerfeld theory) was an extension of the Bohr model to allow elliptical orbits of electrons around an atomic nucleus. Bohr–Sommerfeld theory is named after Danish physicist Niels Bohr and German physicist Arnold Sommerfeld. Sommerfeld showed that, if electronic orbits are elliptical instead of circular (as in Bohr's model of the atom), the fine-structure of the hydrogen atom can be described.
The Bohr–Sommerfeld model added to the quantized angular momentum condition of the Bohr model with a radial quantization (condition by William Wilson, the Wilson–Sommerfeld quantization condition):
where pr is the radial momentum canonically conjugate to the coordinate q, which is the radial position, and T is one full orbital period. The integral is the action of action-angle coordinates. This condition, suggested by the correspondence principle, is the only one possible, since the quantum numbers are adiabatic invariants.

History
Main article: Old quantum theoryIn 1913, Niels Bohr displayed rudiments of the later defined correspondence principle and used it to formulate a model of the hydrogen atom which explained its line spectrum. In the next few years Arnold Sommerfeld extended the quantum rule to arbitrary integrable systems making use of the principle of adiabatic invariance of the quantum numbers introduced by Hendrik Lorentz and Albert Einstein. Sommerfeld made a crucial contribution by quantizing the z-component of the angular momentum, which in the old quantum era was called "space quantization" (German: Richtungsquantelung). This allowed the orbits of the electron to be ellipses instead of circles, and introduced the concept of quantum degeneracy. The theory would have correctly explained the Zeeman effect, except for the issue of electron spin. Sommerfeld's model was much closer to the modern quantum mechanical picture than Bohr's.
In the 1950s Joseph Keller updated Bohr–Sommerfeld quantization using Einstein's interpretation of 1917, now known as Einstein–Brillouin–Keller method. In 1971, Martin Gutzwiller took into account that this method only works for integrable systems and derived a semiclassical way of quantizing chaotic systems from path integrals.
Predictions
The Sommerfeld model predicted that the magnetic moment of an atom measured along an axis will only take on discrete values, a result which seems to contradict rotational invariance but which was confirmed by the Stern–Gerlach experiment. This was a significant step in the development of quantum mechanics. It also described the possibility of atomic energy levels being split by a magnetic field (called the Zeeman effect). Walther Kossel worked with Bohr and Sommerfeld on the Bohr–Sommerfeld model of the atom introducing two electrons in the first shell and eight in the second.
Issues
The Bohr–Sommerfeld model was fundamentally inconsistent and led to many paradoxes. The magnetic quantum number measured the tilt of the orbital plane relative to the xy plane, and it could only take a few discrete values. This contradicted the obvious fact that an atom could be turned this way and that relative to the coordinates without restriction. The Sommerfeld quantization can be performed in different canonical coordinates and sometimes gives different answers. The incorporation of radiation corrections was difficult, because it required finding action-angle coordinates for a combined radiation/atom system, which is difficult when the radiation is allowed to escape. The whole theory did not extend to non-integrable motions, which meant that many systems could not be treated even in principle. In the end, the model was replaced by the modern quantum-mechanical treatment of the hydrogen atom, which was first given by Wolfgang Pauli in 1925, using Heisenberg's matrix mechanics. The current picture of the hydrogen atom is based on the atomic orbitals of wave mechanics, which Erwin Schrödinger developed in 1926.
However, this is not to say that the Bohr–Sommerfeld model was without its successes. Calculations based on the Bohr–Sommerfeld model were able to accurately explain a number of more complex atomic spectral effects. For example, up to first-order perturbations, the Bohr model and quantum mechanics make the same predictions for the spectral line splitting in the Stark effect. At higher-order perturbations, however, the Bohr model and quantum mechanics differ, and measurements of the Stark effect under high field strengths helped confirm the correctness of quantum mechanics over the Bohr model. The prevailing theory behind this difference lies in the shapes of the orbitals of the electrons, which vary according to the energy state of the electron.
The Bohr–Sommerfeld quantization conditions lead to questions in modern mathematics. Consistent semiclassical quantization condition requires a certain type of structure on the phase space, which places topological limitations on the types of symplectic manifolds which can be quantized. In particular, the symplectic form should be the curvature form of a connection of a Hermitian line bundle, which is called a prequantization.
Relativistic orbit

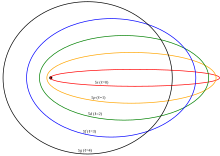
Arnold Sommerfeld derived the relativistic solution of atomic energy levels. We will start this derivation with the relativistic equation for energy in the electric potential
After substitution we get
For momentum , and their ratio the equation of motion is (see Binet equation)
with solution
The angular shift of periapsis per revolution is given by
With the quantum conditions
and
we will obtain energies
where is the fine-structure constant. This solution (using substitutions for quantum numbers) is equivalent to the solution of the Dirac equation. Nevertheless, both solutions fail to predict the Lamb shifts.
See also
References
- ^ Kramers, Hendrik Anthony (1923). The atom and the Bohr theory of its structure : an elementary presentation. MIT Libraries. New York : A.A. Knopf.
- ^ Sommerfeld, Arnold Johannes Wilhelm (1921). Atombau und Spektrallinien. University of California. Braunschweig : F. Vieweg & Sohn.
- A. Sommerfeld (1916). "Zur Quantentheorie der Spektrallinien". Annalen der Physik (in German). 51 (17): 1–94. Bibcode:1916AnP...356....1S. doi:10.1002/andp.19163561702.
- W. Wilson (1915). "The quantum theory of radiation and line spectra". Philosophical Magazine. 29 (174): 795–802. doi:10.1080/14786440608635362.
- ^ Sommerfeld, Arnold (1919). Atombau und Spektrallinien'. Braunschweig: Friedrich Vieweg und Sohn. ISBN 978-3-87144-484-5.
- The Collected Papers of Albert Einstein, vol. 6, A. Engel, trans., Princeton U. Press, Princeton, NJ (1997), p. 434
- Stone, A.D. (August 2005). "Einstein's unknown insight and the problem of quantizing chaos" (PDF). Physics Today. 58 (8): 37–43. Bibcode:2005PhT....58h..37S. doi:10.1063/1.2062917.
- Heilbron, John L. (1967). "The Kossel-Sommerfeld Theory and the Ring Atom". Isis. 58 (4): 450–485. doi:10.1086/350299. JSTOR 228422. S2CID 144639796.
- Bohr, N. (July 1923). "The Structure of the Atom". Nature. 112 (2801): 29–44. doi:10.1038/112029a0. ISSN 1476-4687.
- https://archive.org/details/atombauundspekt00sommgoog/page/n541 - Atombau und Spektrallinien, 1921, page 520
- Ya I Granovski (2004). "Sommerfeld formula and Dirac's theory" (PDF). Physics-Uspekhi. 47 (5): 523–524. Bibcode:2004PhyU...47..523G. doi:10.1070/PU2004v047n05ABEH001885. S2CID 250900220.



 we get
we get

 ,
,  and their ratio
and their ratio  the equation of motion is (see
the equation of motion is (see 





 is the
is the