| This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (November 2019) (Learn how and when to remove this message) |
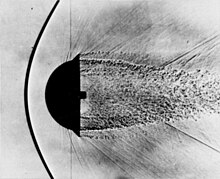
A bow shock, also called a detached shock or bowed normal shock, is a curved propagating disturbance wave characterized by an abrupt, nearly discontinuous, change in pressure, temperature, and density. It occurs when a supersonic flow encounters a body, around which the necessary deviation angle of the flow is higher than the maximum achievable deviation angle for an attached oblique shock (see detachment criterion). Then, the oblique shock transforms in a curved detached shock wave. As bow shocks occur for high flow deflection angles, they are often seen forming around blunt bodies, because of the high deflection angle that the body impose to the flow around it.
The thermodynamic transformation across a bow shock is non-isentropic and the shock decreases the flow velocity from supersonic velocity upstream to subsonic velocity downstream.
Applications
The bow shock significantly increases the drag in a vehicle traveling at a supersonic speed. This property was utilized in the design of the return capsules during space missions such as the Apollo program, which need a high amount of drag in order to slow down during atmospheric reentry.
Shock relations
As in normal shock and oblique shock,
- The upstream static pressures is lower than the downstream static pressure.
- The upstream static density is lower than the downstream static density.
- The upstream static temperature is lower than the downstream static temperature.
- The upstream total pressure is greater than the downstream total pressure.
- The upstream total density is lower than the downstream total density.
- The upstream total temperature is equal to the downstream total temperature, as the shock wave is supposed isenthalpic.
For a curved shock, the shock angle varies and thus has variable strength across the entire shock front. The post-shock flow velocity and vorticity can therefore be computed via the Crocco's theorem, which is independent of any EOS (equation of state) assuming inviscid flow.
See also
References
- Ben-Dor, G. (2007). Shock Wave Reflection Phenomena. Shock Wave and High Pressure Phenomena. Bibcode:2007swrp.book.....B. doi:10.1007/978-3-540-71382-1. ISBN 978-3-540-71381-4.
- Supersonic Flow and Shock Waves.
- Landau, L.D.; Lifshitz, E.M. (2005) . Fluid Mechanics 2nd edition. Elsevier. ISBN 978-0-7506-2767-2.
- Courant, R.; Friedrichs, K.O. (1956) . Supersonic Flow and Shock Waves. New York: Interscience Publishers.