Misplaced Pages

A Brownian snake is a stochastic Markov process on the space of stopped paths. It has been extensively studied., and was in particular successfully used as a representation of superprocesses.

Informally, superprocesses are the scaling limit of branching processes, except each particle splits and dies at infinite rates. The Brownian snake is a stochastic object that enables the representation of the genealogy of a superprocess, providing a link between super-Brownian motion and Brownian trees. In other words, even though infinitely many particles are constantly born, we can still keep track of individual trajectories in space, or of when two given present-day particles have split from a common ancestor in the past.

History

The Brownian snake approach was originally developed by Jean-François Le Gall. It has since been applied in fragmentation theory, partial differential equation or planar map

The simplest setting

Let ${\displaystyle D(\mathbb {R} _{+},\mathbb {R} )}$ be the space of càdlàg functions from ${\displaystyle \mathbb {R} _{+}}$ to ${\displaystyle \mathbb {R} }$, equipped with a metric ${\displaystyle d}$ compatible with the Skorokhod topology. We define a stopped path as a couple ${\displaystyle (w,z)}$ where ${\displaystyle w\in D(\mathbb {R} _{+},\mathbb {R} )}$ and ${\displaystyle z\in \mathbb {R} _{+}}$ are such that ${\displaystyle w(t)=w(t\wedge z)}$. In other words, ${\displaystyle w}$ is constant after ${\displaystyle z}$.

Now, we consider a jump process ${\displaystyle (J_{s}^{N})_{s\geq 0}}$ with states ${\displaystyle \{+1,-1\}}$ and jump rate ${\displaystyle N}$, such that ${\displaystyle J_{0}^{N}=+1}$. We set:$${\displaystyle {\hat {\beta }}_{s}^{N}:=\int _{0}^{s}J_{s'}^{N}ds'}$$and then ${\displaystyle \beta _{s}^{N}:=|{\hat {\beta }}_{s}^{N}|}$ to be the process reflected on 0.

In words, ${\displaystyle \beta _{s}^{N}}$ increases with speed 1, until ${\displaystyle J_{s}^{N}}$ jumps, in which case it decreases with speed 1, and so on. We define the stopping time ${\displaystyle \sigma _{N}}$ to be the ${\displaystyle N}$-th hitting time of 0 by ${\displaystyle \beta ^{N}}$. We now define a stochastic process ${\displaystyle (\eta _{s}^{N},\beta _{s}^{N})_{s\in \mathbb {R} _{+}}}$ on the set of stopped paths as follows:

• ${\displaystyle \eta _{0}^{N}=0}$
• if ${\displaystyle J_{s}^{N}=+1}$ for ${\displaystyle s\in }$ then:
  • ${\displaystyle \eta _{s_{1}}(t)=\eta _{s_{2}}(t)}$ for ${\displaystyle t\leq \beta _{s_{1}}}$
  • ${\displaystyle {\Big (}\eta _{s_{2}}(t-\beta _{s_{1}})-\eta _{s_{1}}(\beta _{s_{1}}){\Big )}_{0\leq t\leq \beta _{s_{2}}-\beta _{s_{1}}}}$ is distributed as a Brownian motion independent from ${\displaystyle \eta _{s_{1}}}$
• if ${\displaystyle J_{s}^{N}=-1}$ for ${\displaystyle s\in }$ then ${\displaystyle \eta _{s_{1}}(t)=\eta _{s_{2}}(t)}$ for ${\displaystyle t\leq \beta _{s_{2}}}$

See animation for an illustration. We call this process a snake and ${\displaystyle \beta _{s}^{N}}$ the head of the snake. This process is not yet the Brownian snake, but a good introduction. The path is erased when the snake head moves backwards, and is created anew when it moves forward.

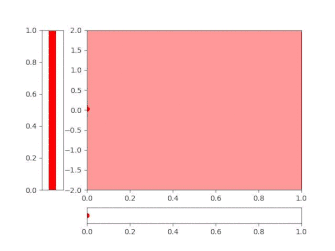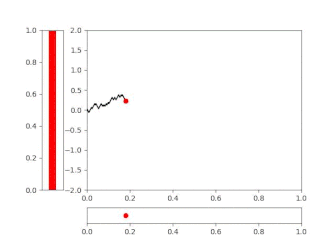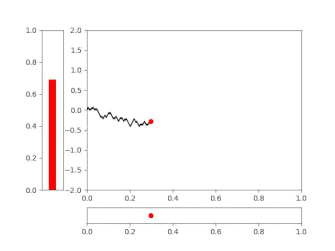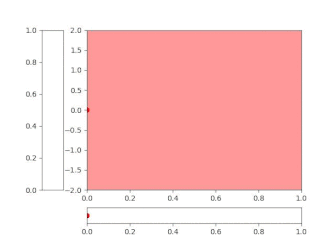
Duality with a branching Brownian motion

We now consider a measure-valued branching process ${\displaystyle (X_{t}^{N})_{t\geq 0}}$ starting with ${\displaystyle N}$ particles, such that each particle dies with rate ${\displaystyle N}$, and upon its death gives birth to two offspring with probability ${\displaystyle 1/2}$.

On the other hand, we may define from our process ${\displaystyle (\eta _{s}^{N},\beta _{s}^{N})_{0\leq s\leq \sigma ^{N}}}$ a measure-valued random process ${\displaystyle {\hat {X}}_{t}}$ as follows: note that for any ${\displaystyle t\in \mathbb {R} _{+}}$, there will almost surely be finitely many times ${\displaystyle s_{1},s_{2},\dots ,s_{n}\in }$ such that ${\displaystyle \beta _{s_{i}}=t}$. We then set for any measurable function ${\displaystyle f}$:

${\displaystyle {\hat {X}}_{t}^{N}(f):=\sum \limits _{i=1}^{n}f(\eta _{s}^{N}(t))}$

Then ${\displaystyle X}$ and ${\displaystyle {\hat {X}}}$ are equal in distribution.

The Brownian snake

We take the limit of the previous system as ${\displaystyle N\to \infty }$. In this setting, the head of the snake keeps jittering. In fact, the process ${\displaystyle \beta _{s}^{N}}$ tends towards a reflected Brownian motion ${\displaystyle \beta _{s}}$. The definitions are no longer valid for a number of reasons, in particular because ${\displaystyle \beta _{s}}$ is almost surely never monotonous on any interval.

However, we may define a probability ${\displaystyle R_{a,b}((u,y),d(w,z))}$ on stopped paths such that:

• ${\displaystyle R_{a,b}}$-almost surely ${\displaystyle z=b}$ and ${\displaystyle w(t)=u(t)}$ for ${\displaystyle 0\leq t\leq a}$
• The law of ${\displaystyle (w(a+t))_{0\leq t\leq b-a}}$ is the law of a standard Brownian motion.

We may also define ${\displaystyle \gamma _{s}^{y}(da,db)}$ to be the distribution of ${\displaystyle (\inf _{0\leq r\leq s}\beta _{r},\beta _{s})}$ if ${\displaystyle \beta _{0}=y}$. Finally, define the transition semigroup on the set of stopped paths:

${\displaystyle Q_{s}((u,y),d(w,z))=\int \gamma _{s}^{y}(da,db)R_{a,b}((u,y),d(w,z))}$

A stochastic process with this semigroup is called a Brownian snake.

We may again find a duality between this process and a branching process. Here the branching process will be a super-Brownian motion ${\displaystyle (X_{t})_{t\in \mathbb {R} _{+}}}$ with branching mechanism ${\displaystyle \phi (z)=z^{2}}$, started on a Dirac in 0.

However, unlike the previous case, we must be more careful in the definition of the process ${\displaystyle {\hat {X}}}$. Indeed, for ${\displaystyle t\in \mathbb {R} _{+}}$ we cannot just list the times ${\displaystyle s_{1},s_{2},\dots }$ such that ${\displaystyle \beta _{s}=t}$. Instead we use the local time ${\displaystyle l_{s}(t)}$ associated with ${\displaystyle \beta _{s}}$: we first define the stopping time ${\displaystyle \sigma =\inf\{s\geq 0,l_{s}(0)\geq u\}}$. Then we define for any measurable ${\displaystyle f}$:$${\displaystyle {\hat {X}}_{t}(f):=\int _{0}^{\sigma }f(\eta _{s}(t))dl_{s}(t)}$$ Then, as before, we obtain that ${\displaystyle X}$ and ${\displaystyle {\hat {X}}}$ are equal in distribution. See the animation for the construction of the branching process from the Brownian snake.

Generalisation

The previous example can be generalized in many ways:

• We may consider ${\displaystyle D(\mathbb {R} _{+},E)}$ where ${\displaystyle (E,d)}$ is a complete separable metric space.
• Instead of a Brownian motion, the underlying movement of the snake can be very general class of Markov processes (see Superprocess).

Link with genealogy and the Brownian tree

The Brownian snake can be seen as a way to represent the genealogy of a superprocess, the same way a Galton-Watson tree may encode the hidden genealogy of a Galton–Watson process. Indeed, for two points of the Brownian snake, their common ancestor will be the infimum of the snake's head position between them.

If we take a Brownian snake and construct a real tree from it, we obtain a Brownian tree.

References

1. Li, Zenghu (2011), Li, Zenghu (ed.), "Measure-Valued Branching Processes", Measure-Valued Branching Markov Processes, Probability and Its Applications, Berlin, Heidelberg: Springer, pp. 29–56, doi:10.1007/978-3-642-15004-3_2, ISBN 978-3-642-15004-3, retrieved 2022-12-20
2. ^ Le Gall, Jean-Francois (1999-07-01). Spatial Branching Processes, Random Snakes and Partial Differential Equations. Springer Science & Business Media. ISBN 978-3-7643-6126-6.
3. Le Gall, Jean-Francois (1991). "Brownian Excursions, Trees and Measure-Valued Branching Processes". The Annals of Probability. 19 (4): 1399–1439. ISSN 0091-1798. JSTOR 2244522.
4. Abraham, Romain; Serlet, Laurent (2002-07-01). "Poisson Snake and Fragmentation". Electronic Journal of Probability. 7 (none). doi:10.1214/EJP.v7-116. ISSN 1083-6489. S2CID 12003800.
5. Abraham, Romain (2000-10-01). "Reflecting Brownian snake and a Neumann–Dirichlet problem". Stochastic Processes and Their Applications. 89 (2): 239–260. doi:10.1016/S0304-4149(00)00027-2. ISSN 0304-4149.
6. Le Gall, Jean-François (2019-09-01). "Brownian geometry". Japanese Journal of Mathematics. 14 (2): 135–174. doi:10.1007/s11537-019-1821-7. ISSN 1861-3624. S2CID 255314865.
7. Miermont, Grégory (2013). "The Brownian map is the scaling limit of uniform random plane quadrangulations". Acta Mathematica. 210 (2): 319–401. arXiv:1104.1606. doi:10.1007/s11511-013-0096-8. ISSN 0001-5962. S2CID 119140342.

• Markov processes