In mathematics, physics and engineering, the sinc function, denoted by sinc(x), has two forms, normalized and unnormalized.
| Sinc | |
|---|---|
 Part of the normalized sinc (blue) and unnormalized sinc function (red) shown on the same scale Part of the normalized sinc (blue) and unnormalized sinc function (red) shown on the same scale | |
| General information | |
| General definition | |
| Motivation of invention | Telecommunication |
| Date of solution | 1952 |
| Fields of application | Signal processing, spectroscopy |
| Domain, codomain and image | |
| Domain | |
| Image | |
| Basic features | |
| Parity | Even |
| Specific values | |
| At zero | 1 |
| Value at +∞ | 0 |
| Value at −∞ | 0 |
| Maxima | 1 at |
| Minima | at |
| Specific features | |
| Root | |
| Related functions | |
| Reciprocal | |
| Derivative | |
| Antiderivative | |
| Series definition | |
| Taylor series | |
In mathematics, the historical unnormalized sinc function is defined for x ≠ 0 by
Alternatively, the unnormalized sinc function is often called the sampling function, indicated as Sa(x).
In digital signal processing and information theory, the normalized sinc function is commonly defined for x ≠ 0 by
In either case, the value at x = 0 is defined to be the limiting value for all real a ≠ 0 (the limit can be proven using the squeeze theorem).
The normalization causes the definite integral of the function over the real numbers to equal 1 (whereas the same integral of the unnormalized sinc function has a value of π). As a further useful property, the zeros of the normalized sinc function are the nonzero integer values of x.
The normalized sinc function is the Fourier transform of the rectangular function with no scaling. It is used in the concept of reconstructing a continuous bandlimited signal from uniformly spaced samples of that signal.
The only difference between the two definitions is in the scaling of the independent variable (the x axis) by a factor of π. In both cases, the value of the function at the removable singularity at zero is understood to be the limit value 1. The sinc function is then analytic everywhere and hence an entire function.
The function has also been called the cardinal sine or sine cardinal function. The term sinc /ˈsɪŋk/ was introduced by Philip M. Woodward in his 1952 article "Information theory and inverse probability in telecommunication", in which he said that the function "occurs so often in Fourier analysis and its applications that it does seem to merit some notation of its own", and his 1953 book Probability and Information Theory, with Applications to Radar. The function itself was first mathematically derived in this form by Lord Rayleigh in his expression (Rayleigh's formula) for the zeroth-order spherical Bessel function of the first kind.
Properties
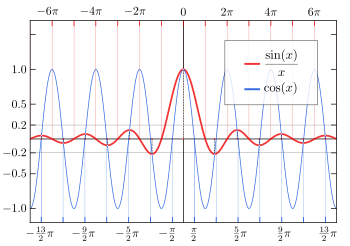
The zero crossings of the unnormalized sinc are at non-zero integer multiples of π, while zero crossings of the normalized sinc occur at non-zero integers.
The local maxima and minima of the unnormalized sinc correspond to its intersections with the cosine function. That is, sin(ξ)/ξ = cos(ξ) for all points ξ where the derivative of sin(x)/x is zero and thus a local extremum is reached. This follows from the derivative of the sinc function:
The first few terms of the infinite series for the x coordinate of the n-th extremum with positive x coordinate are where and where odd n lead to a local minimum, and even n to a local maximum. Because of symmetry around the y axis, there exist extrema with x coordinates −xn. In addition, there is an absolute maximum at ξ0 = (0, 1).
The normalized sinc function has a simple representation as the infinite product:

and is related to the gamma function Γ(x) through Euler's reflection formula:
Euler discovered that and because of the product-to-sum identity
Euler's product can be recast as a sum
The continuous Fourier transform of the normalized sinc (to ordinary frequency) is rect(f): where the rectangular function is 1 for argument between −1/2 and 1/2, and zero otherwise. This corresponds to the fact that the sinc filter is the ideal (brick-wall, meaning rectangular frequency response) low-pass filter.
This Fourier integral, including the special case is an improper integral (see Dirichlet integral) and not a convergent Lebesgue integral, as
The normalized sinc function has properties that make it ideal in relationship to interpolation of sampled bandlimited functions:
- It is an interpolating function, i.e., sinc(0) = 1, and sinc(k) = 0 for nonzero integer k.
- The functions xk(t) = sinc(t − k) (k integer) form an orthonormal basis for bandlimited functions in the function space L(R), with highest angular frequency ωH = π (that is, highest cycle frequency fH = 1/2).
Other properties of the two sinc functions include:
- The unnormalized sinc is the zeroth-order spherical Bessel function of the first kind, j0(x). The normalized sinc is j0(πx).
- where Si(x) is the sine integral,
- λ sinc(λx) (not normalized) is one of two linearly independent solutions to the linear ordinary differential equation The other is cos(λx)/x, which is not bounded at x = 0, unlike its sinc function counterpart.
- Using normalized sinc,
- The following improper integral involves the (not normalized) sinc function:
Relationship to the Dirac delta distribution
The normalized sinc function can be used as a nascent delta function, meaning that the following weak limit holds:
This is not an ordinary limit, since the left side does not converge. Rather, it means that
for every Schwartz function, as can be seen from the Fourier inversion theorem. In the above expression, as a → 0, the number of oscillations per unit length of the sinc function approaches infinity. Nevertheless, the expression always oscillates inside an envelope of ±1/πx, regardless of the value of a.
This complicates the informal picture of δ(x) as being zero for all x except at the point x = 0, and illustrates the problem of thinking of the delta function as a function rather than as a distribution. A similar situation is found in the Gibbs phenomenon.
Summation
All sums in this section refer to the unnormalized sinc function.
The sum of sinc(n) over integer n from 1 to ∞ equals π − 1/2:
The sum of the squares also equals π − 1/2:
When the signs of the addends alternate and begin with +, the sum equals 1/2:
The alternating sums of the squares and cubes also equal 1/2:
Series expansion
The Taylor series of the unnormalized sinc function can be obtained from that of the sine (which also yields its value of 1 at x = 0):
The series converges for all x. The normalized version follows easily:
Euler famously compared this series to the expansion of the infinite product form to solve the Basel problem.
Higher dimensions
The product of 1-D sinc functions readily provides a multivariate sinc function for the square Cartesian grid (lattice): sincC(x, y) = sinc(x) sinc(y), whose Fourier transform is the indicator function of a square in the frequency space (i.e., the brick wall defined in 2-D space). The sinc function for a non-Cartesian lattice (e.g., hexagonal lattice) is a function whose Fourier transform is the indicator function of the Brillouin zone of that lattice. For example, the sinc function for the hexagonal lattice is a function whose Fourier transform is the indicator function of the unit hexagon in the frequency space. For a non-Cartesian lattice this function can not be obtained by a simple tensor product. However, the explicit formula for the sinc function for the hexagonal, body-centered cubic, face-centered cubic and other higher-dimensional lattices can be explicitly derived using the geometric properties of Brillouin zones and their connection to zonotopes.
For example, a hexagonal lattice can be generated by the (integer) linear span of the vectors
Denoting one can derive the sinc function for this hexagonal lattice as
This construction can be used to design Lanczos window for general multidimensional lattices.
Sinhc
Some authors, by analogy, define the hyperbolic sine cardinal function.
See also
- Anti-aliasing filter – Mathematical transformation reducing the damage caused by aliasing
- Borwein integral – Type of mathematical integrals
- Dirichlet integral – Integral of sin(x)/x from 0 to infinity.
- Lanczos resampling – Application of a mathematical formula
- List of mathematical functions
- Shannon wavelet
- Sinc filter – Ideal low-pass filter or averaging filter
- Sinc numerical methods
- Trigonometric functions of matrices – Important functions in solving differential equations
- Trigonometric integral – Special function defined by an integral
- Whittaker–Shannon interpolation formula – Signal (re-)construction algorithm
- Winkel tripel projection – Pseudoazimuthal compromise map projection (cartography)
References
- Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W., eds. (2010), "Numerical methods", NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248..
- Singh, R. P.; Sapre, S. D. (2008). Communication Systems, 2E (illustrated ed.). Tata McGraw-Hill Education. p. 15. ISBN 978-0-07-063454-1. Extract of page 15
- Weisstein, Eric W. "Sinc Function". mathworld.wolfram.com. Retrieved 2023-06-07.
- Merca, Mircea (2016-03-01). "The cardinal sine function and the Chebyshev–Stirling numbers". Journal of Number Theory. 160: 19–31. doi:10.1016/j.jnt.2015.08.018. ISSN 0022-314X. S2CID 124388262.
- Woodward, P. M.; Davies, I. L. (March 1952). "Information theory and inverse probability in telecommunication" (PDF). Proceedings of the IEE - Part III: Radio and Communication Engineering. 99 (58): 37–44. doi:10.1049/pi-3.1952.0011.
- Poynton, Charles A. (2003). Digital video and HDTV. Morgan Kaufmann Publishers. p. 147. ISBN 978-1-55860-792-7.
- Woodward, Phillip M. (1953). Probability and information theory, with applications to radar. London: Pergamon Press. p. 29. ISBN 978-0-89006-103-9. OCLC 488749777.
- Euler, Leonhard (1735). "On the sums of series of reciprocals". arXiv:math/0506415.
- Luis Ortiz-Gracia; Cornelis W. Oosterlee (2016). "A highly efficient Shannon wavelet inverse Fourier technique for pricing European options". SIAM J. Sci. Comput. 38 (1): B118 – B143. Bibcode:2016SJSC...38B.118O. doi:10.1137/15M1014164. hdl:2072/377498.
- "Advanced Problem 6241". American Mathematical Monthly. 87 (6). Washington, DC: Mathematical Association of America: 496–498. June–July 1980. doi:10.1080/00029890.1980.11995075.
- Robert Baillie; David Borwein; Jonathan M. Borwein (December 2008). "Surprising Sinc Sums and Integrals". American Mathematical Monthly. 115 (10): 888–901. doi:10.1080/00029890.2008.11920606. hdl:1959.13/940062. JSTOR 27642636. S2CID 496934.
- Baillie, Robert (2008). "Fun with Fourier series". arXiv:0806.0150v2 .
- ^ Ye, W.; Entezari, A. (June 2012). "A Geometric Construction of Multivariate Sinc Functions". IEEE Transactions on Image Processing. 21 (6): 2969–2979. Bibcode:2012ITIP...21.2969Y. doi:10.1109/TIP.2011.2162421. PMID 21775264. S2CID 15313688.
- Ainslie, Michael (2010). Principles of Sonar Performance Modelling. Springer. p. 636. ISBN 9783540876625.
- Günter, Peter (2012). Nonlinear Optical Effects and Materials. Springer. p. 258. ISBN 9783540497134.
- Schächter, Levi (2013). Beam-Wave Interaction in Periodic and Quasi-Periodic Structures. Springer. p. 241. ISBN 9783662033982.




 at
at 







 for all real a ≠ 0 (the limit can be proven using the
for all real a ≠ 0 (the limit can be proven using the 
 where
where
 and where odd n lead to a local minimum, and even n to a local maximum. Because of symmetry around the y axis, there exist extrema with x coordinates −xn. In addition, there is an absolute maximum at ξ0 = (0, 1).
and where odd n lead to a local minimum, and even n to a local maximum. Because of symmetry around the y axis, there exist extrema with x coordinates −xn. In addition, there is an absolute maximum at ξ0 = (0, 1).


 and because of the product-to-sum identity
and because of the product-to-sum identity
 Euler's product can be recast as a sum
Euler's product can be recast as a sum

 where the
where the  is an
is an 

 The other is cos(λx)/x, which is not bounded at x = 0, unlike its sinc function counterpart.
The other is cos(λx)/x, which is not bounded at x = 0, unlike its sinc function counterpart.














 one can derive the sinc function for this hexagonal lattice as
one can derive the sinc function for this hexagonal lattice as

