Misplaced Pages

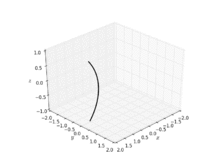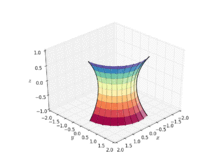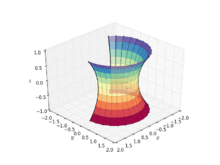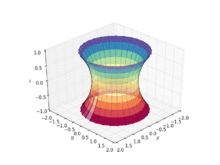
In geometry, a catenoid is a type of surface, arising by rotating a catenary curve about an axis (a surface of revolution). It is a minimal surface, meaning that it occupies the least area when bounded by a closed space. It was formally described in 1744 by the mathematician Leonhard Euler.

Soap film attached to twin circular rings will take the shape of a catenoid. Because they are members of the same associate family of surfaces, a catenoid can be bent into a portion of a helicoid, and vice versa.

Geometry

The catenoid was the first non-trivial minimal surface in 3-dimensional Euclidean space to be discovered apart from the plane. The catenoid is obtained by rotating a catenary about its directrix. It was found and proved to be minimal by Leonhard Euler in 1744.

Early work on the subject was published also by Jean Baptiste Meusnier. There are only two minimal surfaces of revolution (surfaces of revolution which are also minimal surfaces): the plane and the catenoid.

The catenoid may be defined by the following parametric equations: $${\displaystyle {\begin{aligned}x&=c\cosh {\frac {v}{c}}\cos u\\y&=c\cosh {\frac {v}{c}}\sin u\\z&=v\end{aligned}}}$$ where ${\displaystyle u\in [-\pi ,\pi )}$ and ${\displaystyle v\in \mathbb {R} }$ and ${\displaystyle c}$ is a non-zero real constant.

In cylindrical coordinates: $${\displaystyle \rho =c\cosh {\frac {z}{c}},}$$ where ${\displaystyle c}$ is a real constant.

A physical model of a catenoid can be formed by dipping two circular rings into a soap solution and slowly drawing the circles apart.

The catenoid may be also defined approximately by the stretched grid method as a facet 3D model.

Helicoid transformation

Because they are members of the same associate family of surfaces, one can bend a catenoid into a portion of a helicoid without stretching. In other words, one can make a (mostly) continuous and isometric deformation of a catenoid to a portion of the helicoid such that every member of the deformation family is minimal (having a mean curvature of zero). A parametrization of such a deformation is given by the system $${\displaystyle {\begin{aligned}x(u,v)&=\sin \theta \,\cosh v\,\cos u+\cos \theta \,\sinh v\,\sin u\\y(u,v)&=\sin \theta \,\cosh v\,\sin u-\cos \theta \,\sinh v\,\cos u\\z(u,v)&=v\sin \theta +u\cos \theta \end{aligned}}}$$ for ${\displaystyle (u,v)\in (-\pi ,\pi ]\times (-\infty ,\infty )}$, with deformation parameter ${\displaystyle -\pi <\theta \leq \pi }$, where:

• ${\displaystyle \theta =\pi }$ corresponds to a right-handed helicoid,
• ${\displaystyle \theta =\pm \pi /2}$ corresponds to a catenoid, and
• ${\displaystyle \theta =0}$ corresponds to a left-handed helicoid.

References

1. Dierkes, Ulrich; Hildebrandt, Stefan; Sauvigny, Friedrich (2010). Minimal Surfaces. Springer Science & Business Media. p. 141. ISBN 9783642116988.
2. ^ Gullberg, Jan (1997). Mathematics: From the Birth of Numbers. W. W. Norton & Company. p. 538. ISBN 9780393040029.
3. Helveticae, Euler, Leonhard (1952) . Carathëodory Constantin (ed.). Methodus inveniendi lineas curvas: maximi minimive proprietate gaudentes sive solutio problematis isoperimetrici latissimo sensu accepti (in Latin). Springer Science & Business Media. ISBN 3-76431-424-9.{{cite book}}: CS1 maint: multiple names: authors list (link)
4. ^ Colding, T. H.; Minicozzi, W. P. (17 July 2006). "Shapes of embedded minimal surfaces". Proceedings of the National Academy of Sciences. 103 (30): 11106–11111. Bibcode:2006PNAS..10311106C. doi:10.1073/pnas.0510379103. PMC 1544050. PMID 16847265.
5. Meusnier, J. B (1881). Mémoire sur la courbure des surfaces [Memory on the curvature of surfaces.] (PDF) (in French). Bruxelles: F. Hayez, Imprimeur De L'Acdemie Royale De Belgique. pp. 477–510. ISBN 9781147341744.
6. "Catenoid". Wolfram MathWorld. Retrieved 15 January 2017.

Further reading

• Krivoshapko, Sergey; Ivanov, V. N. (2015). "Minimal Surfaces". Encyclopedia of Analytical Surfaces. Springer. ISBN 9783319117737.

External links

• "Catenoid", Encyclopedia of Mathematics, EMS Press, 2001
• Catenoid – WebGL model
• Euler's text describing the catenoid at Carnegie Mellon University
• Calculating the surface area of a Catenoid
• Minimal Surface of Revolution

v t e Minimal surfaces
Associate family Bour's Catalan's Catenoid Chen–Gackstatter Costa's Enneper Gyroid Helicoid Henneberg k-noid Lidinoid Neovius Richmond Riemann's Saddle tower Scherk Schwarz Triply periodic

• Minimal surfaces