The Cauchy convergence test is a method used to test infinite series for convergence. It relies on bounding sums of terms in the series. This convergence criterion is named after Augustin-Louis Cauchy who published it in his textbook Cours d'Analyse 1821.
Statement
A series is convergent if and only if for every there is a natural number such that
holds for all and all .
Explanation
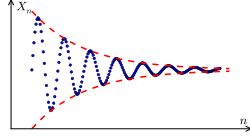 (a) The plot of a Cauchy sequence shown in blue, as versus . If the space containing the sequence is complete, the "ultimate destination" of this sequence (that is, the limit) exists.
(a) The plot of a Cauchy sequence shown in blue, as versus . If the space containing the sequence is complete, the "ultimate destination" of this sequence (that is, the limit) exists.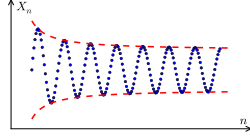 (b) A sequence that is not Cauchy. The elements of the sequence fail to get arbitrarily close to each other as the sequence progresses.
(b) A sequence that is not Cauchy. The elements of the sequence fail to get arbitrarily close to each other as the sequence progresses.| This section does not cite any sources. Please help improve this section by adding citations to reliable sources. Unsourced material may be challenged and removed. (February 2022) (Learn how and when to remove this message) |
The test works because the space of real numbers and the space of complex numbers (with the metric given by the absolute value) are both complete. From here, the series is convergent if and only if the partial sums
are a Cauchy sequence.
Cauchy's convergence test can only be used in complete metric spaces (such as and ), which are spaces where all Cauchy sequences converge. This is because we need only show that its elements become arbitrarily close to each other after a finite progression in the sequence to prove the series converges.
Proof
We can use the results about convergence of the sequence of partial sums of the infinite series and apply them to the convergence of the infinite series itself. The Cauchy Criterion test is one such application. For any real sequence , the above results on convergence imply that the infinite series
converges if and only if for every there is a number N, such that m ≥ n ≥ N imply
Probably the most interesting part of this theorem is that the Cauchy condition implies the existence of the limit: this is indeed related to the completeness of the real line. The Cauchy criterion can be generalized to a variety of situations, which can all be loosely summarized as "a vanishing oscillation condition is equivalent to convergence".
This article incorporates material from Cauchy criterion for convergence on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.
References
- Allegranza, Mauro. "Answer to 'Origin of Cauchy convergence test'". History of Science and Mathematics. StackExchange. Retrieved 10 September 2021.
- Abbott, Stephen (2001). Understanding analysis. Undergraduate Texts in Mathematics. New York, NY: Springer Verlag. p. 63. ISBN 978-0-387-21506-8.
- Wade, William (2010). An Introduction to Analysis. Upper Saddle River, NJ: Prentice Hall. ISBN 9780132296380.
- Kudryavtsev, Lev D.; De Lellis, Camillo; Artemisfowl3rd (2013). "Cauchy criteria". In Rehmann, Ulf (ed.). Encyclopedia of Mathematics. Springer, European Mathematical Society.
{{cite encyclopedia}}: CS1 maint: numeric names: authors list (link)
 is convergent
is convergent  there is a
there is a  such that
such that

 and all
and all  .
.
 shown in blue, as
shown in blue, as  versus
versus  . If the space containing the sequence is complete, the "ultimate destination" of this sequence (that is, the limit) exists.
. If the space containing the sequence is complete, the "ultimate destination" of this sequence (that is, the limit) exists. of
of  of
of 
 , the above results on convergence imply that the
, the above results on convergence imply that the 
