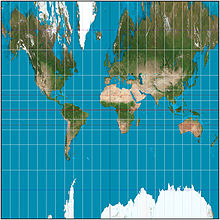

The central cylindrical projection is a perspective cylindrical map projection. It corresponds to projecting the Earth's surface onto a cylinder tangent to the equator as if from a light source at Earth's center. The cylinder is then cut along one of the projected meridians and unrolled into a flat map.
The projection is neither conformal nor equal-area. Distortion increases so rapidly away from the equator that the central cylindrical is only used as an easily understood illustration of projection, rather than for practical maps. Its vertical stretching is even greater than that of the Mercator projection, whose construction method is sometimes erroneously described equivalently to the central cylindrical's. The scale becomes infinite at the poles. It is not known who first developed the projection, but it appeared with other new cylindrical projections in the 19th century, and regularly finds its way into textbooks, chiefly to illustrate that this is not the way the Mercator is constructed. As with any cylindrical projection, the construction can be generalized by positioning the cylinder to be tangent to a great circle of the globe that is not the equator.
This projection has prominent use in panoramic photography, where it is usually called the "cylindrical projection". It can present a full 360° panorama and preserves vertical lines. Unlike other cylindrical projections, it gives correct perspective for tall objects, an important trait for architectural scenes.
Formulae
R denotes the radius of the generating globe; φ is the latitude; λ is the longitude; λ0 is the longitude of the central meridian; and x and y are the mapped coordinates.
See also
References
- ^ Flattening the Earth: Two Thousand Years of Map Projections, John P. Snyder, Chicago University Press, 1993, pp. 106–107, ISBN 0-226-76747-7.
- World Maps and Globes, Irving Fisher and O. M. Miller, Essential Books, 1944, p. 46.
