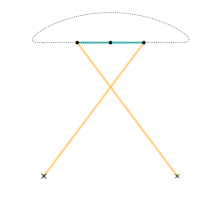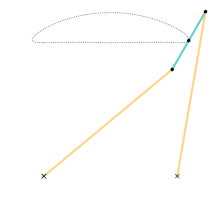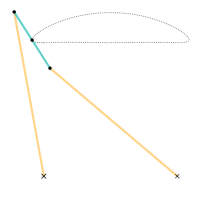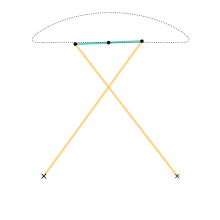
Dimensions (unit length a): Link 3: a + a Links 2 & 4: 5a Link 1 (horizontal distance between ground joints): 4a

In kinematics, Chebyshev's linkage is a four-bar linkage that converts rotational motion to approximate linear motion.
It was invented by the 19th-century mathematician Pafnuty Chebyshev, who studied theoretical problems in kinematic mechanisms. One of the problems was the construction of a linkage that converts a rotary motion into an approximate straight-line motion (a straight line mechanism). This was also studied by James Watt in his improvements to the steam engine, which resulted in Watt's linkage.
Equations of motion
The motion of the linkage can be constrained to an input angle that may be changed through velocities, forces, etc. The input angles can be either link L2 with the horizontal or link L4 with the horizontal. Regardless of the input angle, it is possible to compute the motion of two end-points for link L3 that we will name A and B, and the middle point.
while the motion of point B will be computed with the other angle,
And ultimately, we will write the output angle in terms of the input angle,
Consequently, we can write the motion of point P, using the two points defined above and the definition of the middle point.
Input angles
The limits to the input angles, in both cases, are:
Usage
Chebyshev linkages did not receive widespread usage in steam engines, but are commonly used as the 'Horse head' design of level luffing crane. In this application the approximate straight movement is translated away from the line's midpoint, but it is still essentially the same mechanism.
See also
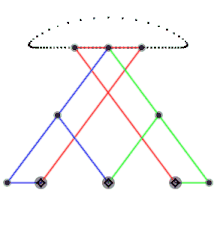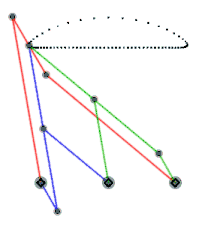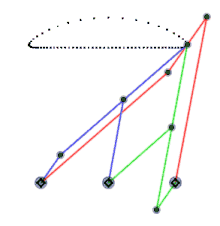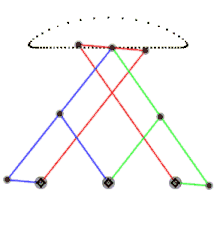
- Chebyshev lambda linkage, the cognate of the Chebyshev linkage.
- Four-bar linkage
- Straight line mechanism
References
- Cornell university – Cross link straight-line mechanism
External links
- Cornell university, "How to draw a straight line, by A.B. Kempe, B.A."
- A simulation Archived 2011-07-25 at the Wayback Machine using the Molecular Workbench software
- A Geogebra simulation of the linkage
- A 3D video of the linkage








