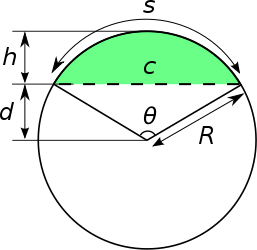
In geometry, a circular segment or disk segment (symbol: ⌓) is a region of a disk which is "cut off" from the rest of the disk by a straight line. The complete line is known as a secant, and the section inside the disk as a chord.
More formally, a circular segment is a plane region bounded by a circular arc (of less than π radians by convention) and the circular chord connecting its endpoints.
Formulae
Let R be the radius of the arc which forms part of the perimeter of the segment, θ the central angle subtending the arc in radians, c the chord length, s the arc length, h the sagitta (height) of the segment, d the apothem of the segment, and a the area of the segment.
Usually, chord length and height are given or measured, and sometimes the arc length as part of the perimeter, and the unknowns are area and sometimes arc length. These can't be calculated simply from chord length and height, so two intermediate quantities, the radius and central angle are usually calculated first.
Radius and central angle
The radius is:
The central angle is
Chord length and height
The chord length and height can be back-computed from radius and central angle by:
The chord length is
The sagitta is
The apothem is
Arc length and area
The arc length, from the familiar geometry of a circle, is
The area a of the circular segment is equal to the area of the circular sector minus the area of the triangular portion (using the double angle formula to get an equation in terms of ):
In terms of R and h,
In terms of c and h,
What can be stated is that as the central angle gets smaller (or alternately the radius gets larger), the area a rapidly and asymptotically approaches . If , is a substantially good approximation.
If is held constant, and the radius is allowed to vary, then we have
As the central angle approaches π, the area of the segment is converging to the area of a semicircle, , so a good approximation is a delta offset from the latter area:
- for h>.75R
As an example, the area is one quarter the circle when θ ~ 2.31 radians (132.3°) corresponding to a height of ~59.6% and a chord length of ~183% of the radius.
Etc.
The perimeter p is the arclength plus the chord length,
As a proportion of the whole area of the disc, , you have
Applications
The area formula can be used in calculating the volume of a partially-filled cylindrical tank lying horizontally.
In the design of windows or doors with rounded tops, c and h may be the only known values and can be used to calculate R for the draftsman's compass setting.
One can reconstruct the full dimensions of a complete circular object from fragments by measuring the arc length and the chord length of the fragment.
To check hole positions on a circular pattern. Especially useful for quality checking on machined products.
For calculating the area or locating the centroid of a planar shape that contains circular segments.
See also
References
- Mathematics distinguishes when necessary between the words circle and disk: a disk is a plane area having a circle as its boundary, while a circle is the closed curve forming the boundary itself.
- These terms refer to a line which intersects a curve. In this case, the curve is the circle forming the disk's boundary.
- The fundamental relationship between , , and derivable directly from the Pythagorean theorem among , , and as components of a right triangle is: which may be solved for , , or as required.
External links
- Definition of a circular segment With interactive animation
- Formulae for area of a circular segment With interactive animation







 ):
):



 . If
. If  ,
,  is a substantially good approximation.
is a substantially good approximation.
 is held constant, and the radius is allowed to vary, then we have
is held constant, and the radius is allowed to vary, then we have
 , so a good approximation is a delta offset from the latter area:
, so a good approximation is a delta offset from the latter area:
 for h>.75R
for h>.75R
 , you have
, you have

 ,
,  derivable directly from the Pythagorean theorem among
derivable directly from the Pythagorean theorem among  , and
, and  as components of a right triangle is:
as components of a right triangle is:  which may be solved for
which may be solved for