Misplaced Pages

Circumcevian triangle

Article snapshot taken from Wikipedia with creative commons attribution-sharealike license. Give it a read and then ask your questions in the chat. We can research this topic together.
Triangle derived from a given triangle and a coplanar point

In Euclidean geometry, a circumcevian triangle is a special triangle associated with a reference triangle and a point in the plane of the triangle. It is also associated with the circumcircle of the reference triangle.

Definition

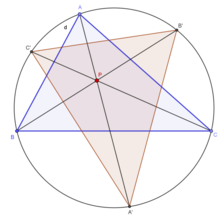
  Reference triangle △ABC   Point P   Circumcircle of △ABC; lines between the vertices of △ABC and P   Circumcevian triangle △A'B'C' of P

Let P be a point in the plane of the reference triangle △ABC. Let the lines AP, BP, CP intersect the circumcircle of △ABC at A', B', C'. The triangle △A'B'C' is called the circumcevian triangle of P with reference to △ABC.

Coordinates

Let a,b,c be the side lengths of triangle △ABC and let the trilinear coordinates of P be α : β : γ. Then the trilinear coordinates of the vertices of the circumcevian triangle of P are as follows: A ′ = − a β γ : ( b γ + c β ) β : ( b γ + c β ) γ B ′ = ( c α + a γ ) α : − b γ α : ( c α + a γ ) γ C ′ = ( a β + b α ) α : ( a β + b α ) β : − c α β {\displaystyle {\begin{array}{rccccc}A'=&-a\beta \gamma &:&(b\gamma +c\beta )\beta &:&(b\gamma +c\beta )\gamma \\B'=&(c\alpha +a\gamma )\alpha &:&-b\gamma \alpha &:&(c\alpha +a\gamma )\gamma \\C'=&(a\beta +b\alpha )\alpha &:&(a\beta +b\alpha )\beta &:&-c\alpha \beta \end{array}}}

Some properties

  • Every triangle inscribed in the circumcircle of the reference triangle ABC is congruent to exactly one circumcevian triangle.
  • The circumcevian triangle of P is similar to the pedal triangle of P.
  • The McCay cubic is the locus of point P such that the circumcevian triangle of P and ABC are orthologic.

See also

References

  1. Kimberling, C (1998). "Triangle Centers and Central Triangles". Congress Numerantium. 129: 201.
  2. ^ Weisstein, Eric W. ""Circumcevian Triangle"". From MathWorld--A Wolfram Web Resource. MathWorld. Retrieved 24 December 2021.
  3. Bernard Gilbert. "K003 McCay Cubic". Catalogue of Triangle Cubics. Bernard Gilbert. Retrieved 24 December 2021.
Category: