
| Recommender systems |
|---|
| Concepts |
| Methods and challenges |
| Implementations |
| Research |
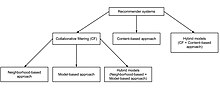
Collaborative filtering (CF) is, besides content-based filtering, one of two major techniques used by recommender systems. Collaborative filtering has two senses, a narrow one and a more general one.
In the newer, narrower sense, collaborative filtering is a method of making automatic predictions (filtering) about a user's interests by utilizing preferences or taste information collected from many users (collaborating). This approach assumes that if persons A and B share similar opinions on one issue, they are more likely to agree on other issues compared to a random pairing of A with another person. For instance, a collaborative filtering system for television programming could predict which shows a user might enjoy based on a limited list of the user's tastes (likes or dislikes). These predictions are specific to the user, but use information gleaned from many users. This differs from the simpler approach of giving an average (non-specific) score for each item of interest, for example based on its number of votes.
In the more general sense, collaborative filtering is the process of filtering information or patterns using techniques involving collaboration among multiple agents, viewpoints, data sources, etc. Applications of collaborative filtering typically involve very large data sets. Collaborative filtering methods have been applied to many kinds of data including: sensing and monitoring data, such as in mineral exploration, environmental sensing over large areas or multiple sensors; financial data, such as financial service institutions that integrate many financial sources; and user data from electronic commerce and web applications.
This article focuses on collaborative filtering for user data, but some of the methods also apply to other major applications.
Overview
The growth of the Internet has made it much more difficult to effectively extract useful information from all the available online information. The overwhelming amount of data necessitates mechanisms for efficient information filtering. Collaborative filtering is one of the techniques used for dealing with this problem.
The motivation for collaborative filtering comes from the idea that people often get the best recommendations from someone with tastes similar to themselves. Collaborative filtering encompasses techniques for matching people with similar interests and making recommendations on this basis.
Collaborative filtering algorithms often require (1) users' active participation, (2) an easy way to represent users' interests, and (3) algorithms that are able to match people with similar interests.
Typically, the workflow of a collaborative filtering system is:
- A user expresses his or her preferences by rating items (e.g. books, movies, or music recordings) of the system. These ratings can be viewed as an approximate representation of the user's interest in the corresponding domain.
- The system matches this user's ratings against other users' and finds the people with most "similar" tastes.
- With similar users, the system recommends items that the similar users have rated highly but not yet being rated by this user (presumably the absence of rating is often considered as the unfamiliarity of an item)
A key problem of collaborative filtering is how to combine and weight the preferences of user neighbors. Sometimes, users can immediately rate the recommended items. As a result, the system gains an increasingly accurate representation of user preferences over time.
Methodology
Collaborative filtering systems have many forms, but many common systems can be reduced to two steps:
- Look for users who share the same rating patterns with the active user (the user whom the prediction is for).
- Use the ratings from those like-minded users found in step 1 to calculate a prediction for the active user
This falls under the category of user-based collaborative filtering. A specific application of this is the user-based Nearest Neighbor algorithm.
Alternatively, item-based collaborative filtering (users who bought x also bought y), proceeds in an item-centric manner:
- Build an item-item matrix determining relationships between pairs of items
- Infer the tastes of the current user by examining the matrix and matching that user's data
See, for example, the Slope One item-based collaborative filtering family.
Another form of collaborative filtering can be based on implicit observations of normal user behavior (as opposed to the artificial behavior imposed by a rating task). These systems observe what a user has done together with what all users have done (what music they have listened to, what items they have bought) and use that data to predict the user's behavior in the future, or to predict how a user might like to behave given the chance. These predictions then have to be filtered through business logic to determine how they might affect the actions of a business system. For example, it is not useful to offer to sell somebody a particular album of music if they already have demonstrated that they own that music.
Relying on a scoring or rating system which is averaged across all users ignores specific demands of a user, and is particularly poor in tasks where there is large variation in interest (as in the recommendation of music). However, there are other methods to combat information explosion, such as web search and data clustering.
Types
Memory-based
The memory-based approach uses user rating data to compute the similarity between users or items. Typical examples of this approach are neighbourhood-based CF and item-based/user-based top-N recommendations. For example, in user based approaches, the value of ratings user u gives to item i is calculated as an aggregation of some similar users' rating of the item:
where U denotes the set of top N users that are most similar to user u who rated item i. Some examples of the aggregation function include:
where k is a normalizing factor defined as , and
where is the average rating of user u for all the items rated by u.
The neighborhood-based algorithm calculates the similarity between two users or items, and produces a prediction for the user by taking the weighted average of all the ratings. Similarity computation between items or users is an important part of this approach. Multiple measures, such as Pearson correlation and vector cosine based similarity are used for this.
The Pearson correlation similarity of two users x, y is defined as
where Ixy is the set of items rated by both user x and user y.
The cosine-based approach defines the cosine-similarity between two users x and y as:
The user based top-N recommendation algorithm uses a similarity-based vector model to identify the k most similar users to an active user. After the k most similar users are found, their corresponding user-item matrices are aggregated to identify the set of items to be recommended. A popular method to find the similar users is the Locality-sensitive hashing, which implements the nearest neighbor mechanism in linear time.
The advantages with this approach include: the explainability of the results, which is an important aspect of recommendation systems; easy creation and use; easy facilitation of new data; content-independence of the items being recommended; good scaling with co-rated items.
There are also several disadvantages of this approach. Its performance decreases when data is sparse, which is common for web-related items. This hinders the scalability of this approach and creates problems with large datasets. Although it can efficiently handle new users because it relies on a data structure, adding new items becomes more complicated because that representation usually relies on a specific vector space. Adding new items requires inclusion of the new item and the re-insertion of all the elements in the structure.
Model-based
An alternative to memory-based methods is to learn models to predict users' rating of unrated items. Model-based CF algorithms include Bayesian networks, clustering models, latent semantic models such as singular value decomposition, probabilistic latent semantic analysis, multiple multiplicative factor, latent Dirichlet allocation and Markov decision process-based models.
Through this approach, dimensionality reduction methods are mostly used for improving robustness and accuracy of memory-based methods. Specifically, methods like singular value decomposition, principal component analysis, known as latent factor models, compress a user-item matrix into a low-dimensional representation in terms of latent factors. This transforms the large matrix that contains many missing values, into a much smaller matrix. A compressed matrix can be used to find neighbors of a user or item as per the previous section. Compression has two advantages in large, sparse data: it is more accurate and scales better.
Hybrid
A number of applications combine the memory-based and the model-based CF algorithms. These overcome the limitations of native CF approaches and improve prediction performance. Importantly, they overcome the CF problems such as sparsity and loss of information. However, they have increased complexity and are expensive to implement. Usually most commercial recommender systems are hybrid, for example, the Google news recommender system.
Deep-learning
In recent years, many neural and deep-learning techniques have been proposed for collaborative filtering. Some generalize traditional matrix factorization algorithms via a non-linear neural architecture, or leverage new model types like Variational Autoencoders. Deep learning has been applied to many scenarios (context-aware, sequence-aware, social tagging etc.).
However, deep learning effectiveness for collaborative recommendation has been questioned. A systematic analysis of publications using deep learning or neural methods to the top-k recommendation problem, published in top conferences (SIGIR, KDD, WWW, RecSys), found that, on average, less than 40% of articles are reproducible, and only 14% in some conferences. Overall, the study identifies 18 articles, only 7 of them could be reproduced and 6 could be outperformed by older and simpler properly tuned baselines. The article highlights potential problems in today's research scholarship and calls for improved scientific practices. Similar issues have been spotted by others and also in sequence-aware recommender systems.
Context-aware collaborative filtering
Many recommender systems simply ignore other contextual information existing alongside user's rating in providing item recommendation. However, by pervasive availability of contextual information such as time, location, social information, and type of the device that user is using, it is becoming more important than ever for a successful recommender system to provide a context-sensitive recommendation. According to Charu Aggrawal, "Context-sensitive recommender systems tailor their recommendations to additional information that defines the specific situation under which recommendations are made. This additional information is referred to as the context."
Taking contextual information into consideration, we will have additional dimension to the existing user-item rating matrix. As an instance, assume a music recommender system which provides different recommendations in corresponding to time of the day. In this case, it is possible a user have different preferences for a music in different time of a day. Thus, instead of using user-item matrix, we may use tensor of order 3 (or higher for considering other contexts) to represent context-sensitive users' preferences.
In order to take advantage of collaborative filtering and particularly neighborhood-based methods, approaches can be extended from a two-dimensional rating matrix into a tensor of higher order. For this purpose, the approach is to find the most similar/like-minded users to a target user; one can extract and compute similarity of slices (e.g. item-time matrix) corresponding to each user. Unlike the context-insensitive case for which similarity of two rating vectors are calculated, in the context-aware approaches, the similarity of rating matrices corresponding to each user is calculated by using Pearson coefficients. After the most like-minded users are found, their corresponding ratings are aggregated to identify the set of items to be recommended to the target user.
The most important disadvantage of taking context into recommendation model is to be able to deal with larger dataset that contains much more missing values in comparison to user-item rating matrix. Therefore, similar to matrix factorization methods, tensor factorization techniques can be used to reduce dimensionality of original data before using any neighborhood-based methods.
Application on social web
Unlike the traditional model of mainstream media, in which there are few editors who set guidelines, collaboratively filtered social media can have a very large number of editors, and content improves as the number of participants increases. Services like Reddit, YouTube, and Last.fm are typical examples of collaborative filtering based media.
One scenario of collaborative filtering application is to recommend interesting or popular information as judged by the community. As a typical example, stories appear in the front page of Reddit as they are "voted up" (rated positively) by the community. As the community becomes larger and more diverse, the promoted stories can better reflect the average interest of the community members.
Misplaced Pages is another application of collaborative filtering. Volunteers contribute to the encyclopedia by filtering out facts from falsehoods.
Another aspect of collaborative filtering systems is the ability to generate more personalized recommendations by analyzing information from the past activity of a specific user, or the history of other users deemed to be of similar taste to a given user. These resources are used as user profiling and helps the site recommend content on a user-by-user basis. The more a given user makes use of the system, the better the recommendations become, as the system gains data to improve its model of that user.
Problems
A collaborative filtering system does not necessarily succeed in automatically matching content to one's preferences. Unless the platform achieves unusually good diversity and independence of opinions, one point of view will always dominate another in a particular community. As in the personalized recommendation scenario, the introduction of new users or new items can cause the cold start problem, as there will be insufficient data on these new entries for the collaborative filtering to work accurately. In order to make appropriate recommendations for a new user, the system must first learn the user's preferences by analysing past voting or rating activities. The collaborative filtering system requires a substantial number of users to rate a new item before that item can be recommended.
Challenges
Data sparsity
In practice, many commercial recommender systems are based on large datasets. As a result, the user-item matrix used for collaborative filtering could be extremely large and sparse, which brings about challenges in the performance of the recommendation.
One typical problem caused by the data sparsity is the cold start problem. As collaborative filtering methods recommend items based on users' past preferences, new users will need to rate a sufficient number of items to enable the system to capture their preferences accurately and thus provides reliable recommendations.
Similarly, new items also have the same problem. When new items are added to the system, they need to be rated by a substantial number of users before they could be recommended to users who have similar tastes to the ones who rated them. The new item problem does not affect content-based recommendations, because the recommendation of an item is based on its discrete set of descriptive qualities rather than its ratings.
Scalability
As the numbers of users and items grow, traditional CF algorithms will suffer serious scalability problems. For example, with tens of millions of customers and millions of items , a CF algorithm with the complexity of is already too large. As well, many systems need to react immediately to online requirements and make recommendations for all users regardless of their millions of users, with most computations happening in very large memory machines.
Synonyms
Synonyms refers to the tendency of a number of the same or very similar items to have different names or entries. Most recommender systems are unable to discover this latent association and thus treat these products differently.
For example, the seemingly different items "children's movie" and "children's film" are actually referring to the same item. Indeed, the degree of variability in descriptive term usage is greater than commonly suspected. The prevalence of synonyms decreases the recommendation performance of CF systems. Topic Modeling (like the Latent Dirichlet Allocation technique) could solve this by grouping different words belonging to the same topic.
Gray sheep
Gray sheep refers to the users whose opinions do not consistently agree or disagree with any group of people and thus do not benefit from collaborative filtering. Black sheep are a group whose idiosyncratic tastes make recommendations nearly impossible. Although this is a failure of the recommender system, non-electronic recommenders also have great problems in these cases, so having black sheep is an acceptable failure.
Shilling attacks
In a recommendation system where everyone can give the ratings, people may give many positive ratings for their own items and negative ratings for their competitors'. It is often necessary for the collaborative filtering systems to introduce precautions to discourage such manipulations.
Diversity and the long tail
Collaborative filters are expected to increase diversity because they help us discover new products. Some algorithms, however, may unintentionally do the opposite. Because collaborative filters recommend products based on past sales or ratings, they cannot usually recommend products with limited historical data. This can create a rich-get-richer effect for popular products, akin to positive feedback. This bias toward popularity can prevent what are otherwise better consumer-product matches. A Wharton study details this phenomenon along with several ideas that may promote diversity and the "long tail." Several collaborative filtering algorithms have been developed to promote diversity and the "long tail" by recommending novel, unexpected, and serendipitous items.
Innovations
- New algorithms have been developed for CF as a result of the Netflix prize.
- Cross-System Collaborative Filtering where user profiles across multiple recommender systems are combined in a multitask manner; this way, preference pattern sharing is achieved across models.
- Robust collaborative filtering, where recommendation is stable towards efforts of manipulation. This research area is still active and not completely solved.
Auxiliary information
User-item matrix is a basic foundation of traditional collaborative filtering techniques, and it suffers from data sparsity problem (i.e. cold start). As a consequence, except for user-item matrix, researchers are trying to gather more auxiliary information to help boost recommendation performance and develop personalized recommender systems. Generally, there are two popular auxiliary information: attribute information and interaction information. Attribute information describes a user's or an item's properties. For example, user attribute might include general profile (e.g. gender and age) and social contacts (e.g. followers or friends in social networks); Item attribute means properties like category, brand or content. In addition, interaction information refers to the implicit data showing how users interplay with the item. Widely used interaction information contains tags, comments or reviews and browsing history etc. Auxiliary information plays a significant role in a variety of aspects. Explicit social links, as a reliable representative of trust or friendship, is always employed in similarity calculation to find similar persons who share interest with the target user. The interaction-associated information – tags – is taken as a third dimension (in addition to user and item) in advanced collaborative filtering to construct a 3-dimensional tensor structure for exploration of recommendation.
See also
- Attention Profiling Mark-up Language (APML)
- Cold start
- Collaborative model
- Collaborative search engine
- Collective intelligence
- Customer engagement
- Delegative Democracy, the same principle applied to voting rather than filtering
- Enterprise bookmarking
- Firefly (website), a defunct website which was based on collaborative filtering
- Filter bubble
- Page rank
- Preference elicitation
- Psychographic filtering
- Recommendation system
- Relevance (information retrieval)
- Reputation system
- Robust collaborative filtering
- Similarity search
- Slope One
- Social translucence
References
- Francesco Ricci and Lior Rokach and Bracha Shapira, Introduction to Recommender Systems Handbook Archived 2 June 2016 at the Wayback Machine, Recommender Systems Handbook, Springer, 2011, pp. 1–35
- ^ Terveen, Loren; Hill, Will (2001). "Beyond Recommender Systems: Helping People Help Each Other" (PDF). Addison-Wesley. p. 6. Retrieved 16 January 2012.
- An integrated approach to TV & VOD Recommendations Archived 6 June 2012 at the Wayback Machine
- John S. Breese, David Heckerman, and Carl Kadie, Empirical Analysis of Predictive Algorithms for Collaborative Filtering, 1998 Archived 19 October 2013 at the Wayback Machine
- Xiaoyuan Su, Taghi M. Khoshgoftaar, A survey of collaborative filtering techniques, Advances in Artificial Intelligence archive, 2009.
- ^ Recommender Systems – The Textbook | Charu C. Aggarwal | Springer. Springer. 2016. ISBN 9783319296579.
- Ghazanfar, Mustansar Ali; Prügel-Bennett, Adam; Szedmak, Sandor (2012). "Kernel-Mapping Recommender system algorithms". Information Sciences. 208: 81–104. CiteSeerX 10.1.1.701.7729. doi:10.1016/j.ins.2012.04.012. S2CID 20328670.
- Das, Abhinandan S.; Datar, Mayur; Garg, Ashutosh; Rajaram, Shyam (2007). "Google news personalization". Proceedings of the 16th international conference on World Wide Web – WWW '07. p. 271. doi:10.1145/1242572.1242610. ISBN 9781595936547. S2CID 207163129.
- He, Xiangnan; Liao, Lizi; Zhang, Hanwang; Nie, Liqiang; Hu, Xia; Chua, Tat-Seng (2017). "Neural Collaborative Filtering". Proceedings of the 26th International Conference on World Wide Web. International World Wide Web Conferences Steering Committee. pp. 173–182. arXiv:1708.05031. doi:10.1145/3038912.3052569. ISBN 9781450349130. S2CID 13907106. Retrieved 16 October 2019.
- Liang, Dawen; Krishnan, Rahul G.; Hoffman, Matthew D.; Jebara, Tony (2018). "Variational Autoencoders for Collaborative Filtering". Proceedings of the 2018 World Wide Web Conference on World Wide Web – WWW '18. International World Wide Web Conferences Steering Committee. pp. 689–698. arXiv:1802.05814. doi:10.1145/3178876.3186150. ISBN 9781450356398.
- Ferrari Dacrema, Maurizio; Cremonesi, Paolo; Jannach, Dietmar (2019). "Are we really making much progress? A worrying analysis of recent neural recommendation approaches". Proceedings of the 13th ACM Conference on Recommender Systems. ACM. pp. 101–109. arXiv:1907.06902. doi:10.1145/3298689.3347058. hdl:11311/1108996. ISBN 9781450362436. S2CID 196831663. Retrieved 16 October 2019.
- Anelli, Vito Walter; Bellogin, Alejandro; Di Noia, Tommaso; Jannach, Dietmar; Pomo, Claudio (2022). "Top-N Recommendation Algorithms: A Quest for the State-of-the-Art". Proceedings of the 30th ACM Conference on User Modeling, Adaptation and Personalization. ACM: 121–131. arXiv:2203.01155. doi:10.1145/3503252.3531292. ISBN 9781450392075. S2CID 247218662. Retrieved 1 March 2022.
- Ludewig, Malte; Mauro, Noemi; Latifi, Sara; Jannach, Dietmar (2019). "Performance comparison of neural and non-neural approaches to session-based recommendation". Proceedings of the 13th ACM Conference on Recommender Systems. ACM. pp. 462–466. doi:10.1145/3298689.3347041. ISBN 9781450362436.
- Adomavicius, Gediminas; Tuzhilin, Alexander (1 January 2015). Ricci, Francesco; Rokach, Lior; Shapira, Bracha (eds.). Recommender Systems Handbook. Springer US. pp. 191–226. doi:10.1007/978-1-4899-7637-6_6. ISBN 9781489976369.
- Bi, Xuan; Qu, Annie; Shen, Xiaotong (2018). "Multilayer tensor factorization with applications to recommender systems". Annals of Statistics. 46 (6B): 3303–3333. arXiv:1711.01598. doi:10.1214/17-AOS1659. S2CID 13677707.
- Zhang, Yanqing; Bi, Xuan; Tang, Niansheng; Qu, Annie (2020). "Dynamic tensor recommender systems". arXiv:2003.05568v1 .
- Bi, Xuan; Tang, Xiwei; Yuan, Yubai; Zhang, Yanqing; Qu, Annie (2021). "Tensors in Statistics". Annual Review of Statistics and Its Application. 8 (1): annurev. Bibcode:2021AnRSA...842720B. doi:10.1146/annurev-statistics-042720-020816. S2CID 224956567.
- Collaborative Filtering: Lifeblood of The Social Web Archived 22 April 2012 at the Wayback Machine
- Gleick, James (2012). The information : a history, a theory, a flood (1st Vintage books ed., 2012 ed.). New York: Vintage Books. p. 410. ISBN 978-1-4000-9623-7. OCLC 745979816.
- Pankaj Gupta, Ashish Goel, Jimmy Lin, Aneesh Sharma, Dong Wang, and Reza Bosagh Zadeh WTF: The who-to-follow system at Twitter, Proceedings of the 22nd international conference on World Wide Web
- Fleder, Daniel; Hosanagar, Kartik (May 2009). "Blockbuster Culture's Next Rise or Fall: The Impact of Recommender Systems on Sales Diversity". Management Science. 55 (5): 697–712. doi:10.1287/mnsc.1080.0974. SSRN 955984.
- Castells, Pablo; Hurley, Neil J.; Vargas, Saúl (2015). "Novelty and Diversity in Recommender Systems". In Ricci, Francesco; Rokach, Lior; Shapira, Bracha (eds.). Recommender Systems Handbook (2 ed.). Springer US. pp. 881–918. doi:10.1007/978-1-4899-7637-6_26. ISBN 978-1-4899-7637-6.
- Choi, Jeongwhan; Hong, Seoyong; Park, Noseong; Cho, Sung-Bae (2022). "Blurring-Sharpening Process Models for Collaborative Filtering". arXiv:2211.09324 .
- Adamopoulos, Panagiotis; Tuzhilin, Alexander (January 2015). "On Unexpectedness in Recommender Systems: Or How to Better Expect the Unexpected". ACM Transactions on Intelligent Systems and Technology. 5 (4): 1–32. doi:10.1145/2559952. S2CID 15282396.
- Adamopoulos, Panagiotis (October 2013). "Beyond rating prediction accuracy". Proceedings of the 7th ACM conference on Recommender systems. pp. 459–462. doi:10.1145/2507157.2508073. ISBN 9781450324090. S2CID 1526264.
- Chatzis, Sotirios (October 2013). "Nonparametric Bayesian multitask collaborative filtering". CIKM '13: Proceedings of the 22nd ACM international conference on Information & Knowledge Management. Portal.acm.org. pp. 2149–2158. doi:10.1145/2505515.2505517. ISBN 9781450322638. S2CID 10515301.
- Mehta, Bhaskar; Hofmann, Thomas; Nejdl, Wolfgang (19 October 2007). Proceedings of the 2007 ACM conference on Recommender systems – Rec Sys '07. Portal.acm.org. p. 49. CiteSeerX 10.1.1.695.1712. doi:10.1145/1297231.1297240. ISBN 9781595937308. S2CID 5640125.
- Shi, Yue; Larson, Martha; Hanjalic, Alan (2014). "Collaborative filtering beyond the user-item matrix: A survey of the state of the art and future challenges". ACM Computing Surveys. 47: 1–45. doi:10.1145/2556270. S2CID 5493334.
- Massa, Paolo; Avesani, Paolo (2009). Computing with social trust. London: Springer. pp. 259–285.
- Groh Georg; Ehmig Christian. Recommendations in taste related domains: collaborative filtering vs. social filtering. Proceedings of the 2007 international ACM conference on Supporting group work. pp. 127–136. CiteSeerX 10.1.1.165.3679.
- Symeonidis, Panagiotis; Nanopoulos, Alexandros; Manolopoulos, Yannis (2008). "Tag recommendations based on tensor dimensionality reduction". Proceedings of the 2008 ACM conference on Recommender systems. pp. 43–50. CiteSeerX 10.1.1.217.1437. doi:10.1145/1454008.1454017. ISBN 9781605580937. S2CID 17911131.
External links
- Beyond Recommender Systems: Helping People Help Each Other, page 12, 2001
- Recommender Systems. Prem Melville and Vikas Sindhwani. In Encyclopedia of Machine Learning, Claude Sammut and Geoffrey Webb (Eds), Springer, 2010.
- Recommender Systems in industrial contexts – PHD thesis (2012) including a comprehensive overview of many collaborative recommender systems
- Toward the next generation of recommender systems: a survey of the state-of-the-art and possible extensions. Adomavicius, G. and Tuzhilin, A. IEEE Transactions on Knowledge and Data Engineering 06.2005
- Evaluating collaborative filtering recommender systems (DOI: 10.1145/963770.963772)
- GroupLens research papers.
- Content-Boosted Collaborative Filtering for Improved Recommendations. Prem Melville, Raymond J. Mooney, and Ramadass Nagarajan. Proceedings of the Eighteenth National Conference on Artificial Intelligence (AAAI-2002), pp. 187–192, Edmonton, Canada, July 2002.
- A collection of past and present "information filtering" projects (including collaborative filtering) at MIT Media Lab
- Eigentaste: A Constant Time Collaborative Filtering Algorithm. Ken Goldberg, Theresa Roeder, Dhruv Gupta, and Chris Perkins. Information Retrieval, 4(2), 133–151. July 2001.
- A Survey of Collaborative Filtering Techniques Su, Xiaoyuan and Khoshgortaar, Taghi. M
- Google News Personalization: Scalable Online Collaborative Filtering Abhinandan Das, Mayur Datar, Ashutosh Garg, and Shyam Rajaram. International World Wide Web Conference, Proceedings of the 16th international conference on World Wide Web
- Factor in the Neighbors: Scalable and Accurate Collaborative Filtering Yehuda Koren, Transactions on Knowledge Discovery from Data (TKDD) (2009)
- Rating Prediction Using Collaborative Filtering
- Recommender Systems Archived 11 February 2013 at the Wayback Machine
- Berkeley Collaborative Filtering



 , and
, and

 is the average rating of user u for all the items rated by u.
is the average rating of user u for all the items rated by u.


 and millions of items
and millions of items  , a CF algorithm with the complexity of
, a CF algorithm with the complexity of  is already too large. As well, many systems need to react immediately to online requirements and make recommendations for all users regardless of their millions of users, with most computations happening in very large memory machines.
is already too large. As well, many systems need to react immediately to online requirements and make recommendations for all users regardless of their millions of users, with most computations happening in very large memory machines.