| This article contains instructions, advice, or how-to content. Please help rewrite the content so that it is more encyclopedic or move it to Wikiversity, Wikibooks, or Wikivoyage. (February 2023) |
| The topic of this article may not meet Misplaced Pages's general notability guideline. Please help to demonstrate the notability of the topic by citing reliable secondary sources that are independent of the topic and provide significant coverage of it beyond a mere trivial mention. If notability cannot be shown, the article is likely to be merged, redirected, or deleted. Find sources: "Computation of cyclic redundancy checks" – news · newspapers · books · scholar · JSTOR (February 2023) (Learn how and when to remove this message) |
Computation of a cyclic redundancy check is derived from the mathematics of polynomial division, modulo two. In practice, it resembles long division of the binary message string, with a fixed number of zeroes appended, by the "generator polynomial" string except that exclusive or operations replace subtractions. Division of this type is efficiently realised in hardware by a modified shift register, and in software by a series of equivalent algorithms, starting with simple code close to the mathematics and becoming faster (and arguably more obfuscated) through byte-wise parallelism and space–time tradeoffs.
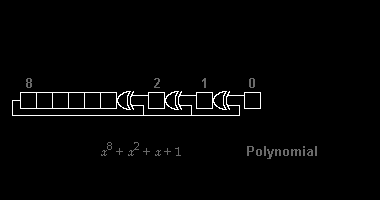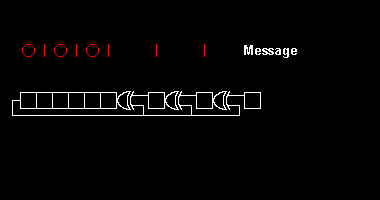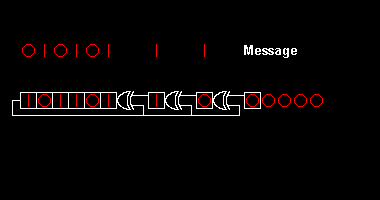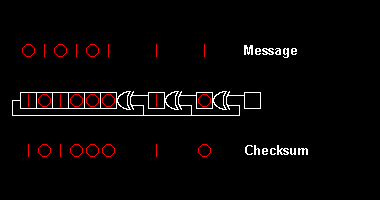

Various CRC standards extend the polynomial division algorithm by specifying an initial shift register value, a final Exclusive-Or step and, most critically, a bit ordering (endianness). As a result, the code seen in practice deviates confusingly from "pure" division, and the register may shift left or right.
Example
For a discussion of polynomial division modulo two, see Mathematics of cyclic redundancy checks.As an example of implementing polynomial division in hardware, suppose that we are trying to compute an 8-bit CRC of an 8-bit message made of the ASCII character "W", which is binary 010101112, decimal 8710, or hexadecimal 5716. For illustration, we will use the CRC-8-ATM (HEC) polynomial . Writing the first bit transmitted (the coefficient of the highest power of ) on the left, this corresponds to the 9-bit string "100000111".
The byte value 5716 can be transmitted in two different orders, depending on the bit ordering convention used. Each one generates a different message polynomial . Msbit-first, this is = 01010111, while lsbit-first, it is = 11101010. These can then be multiplied by to produce two 16-bit message polynomials .
Computing the remainder then consists of subtracting multiples of the generator polynomial . This is just like decimal long division, but even simpler because the only possible multiples at each step are 0 and 1, and the subtractions borrow "from infinity" instead of reducing the upper digits. Because we do not care about the quotient, there is no need to record it.
| Most-significant bit first | Least-significant bit first | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
Observe that after each subtraction, the bits are divided into three groups: at the beginning, a group which is all zero; at the end, a group which is unchanged from the original; and a blue shaded group in the middle which is "interesting". The "interesting" group is 8 bits long, matching the degree of the polynomial. Every step, the appropriate multiple of the polynomial is subtracted to make the zero group one bit longer, and the unchanged group becomes one bit shorter, until only the final remainder is left.
In the msbit-first example, the remainder polynomial is . Converting to a hexadecimal number using the convention that the highest power of x is the msbit; this is A216. In the lsbit-first, the remainder is . Converting to hexadecimal using the convention that the highest power of x is the lsbit, this is 1916.
Implementation
Writing out the full message at each step, as done in the example above, is very tedious. Efficient implementations use an -bit shift register to hold only the interesting bits. Multiplying the polynomial by is equivalent to shifting the register by one place, as the coefficients do not change in value but only move up to the next term of the polynomial.
Here is a first draft of some pseudocode for computing an n-bit CRC. It uses a contrived composite data type for polynomials, where x is not an integer variable, but a constructor generating a Polynomial object that can be added, multiplied and exponentiated. To xor two polynomials is to add them, modulo two; that is, to exclusive OR the coefficients of each matching term from both polynomials.
function crc(bit array bitString, int len) {
remainderPolynomial := polynomialForm(bitString) // First n bits of the message
// A popular variant complements remainderPolynomial here; see § Preset to −1 below
for i from 1 to len {
remainderPolynomial := remainderPolynomial * x + bitString * x // Define bitString=0 for k>len
if coefficient of x of remainderPolynomial = 1 {
remainderPolynomial := remainderPolynomial xor generatorPolynomial
}
}
// A popular variant complements remainderPolynomial here; see § Post-invert below
return remainderPolynomial
}
- Code fragment 1: Simple polynomial division
Note that this example code avoids the need to specify a bit-ordering convention by not using bytes; the input bitString is already in the form of a bit array, and the remainderPolynomial is manipulated in terms of polynomial operations; the multiplication by could be a left or right shift, and the addition of bitString is done to the coefficient, which could be the right or left end of the register.
This code has two disadvantages. First, it actually requires an n+1-bit register to hold the remainderPolynomial so that the coefficient can be tested. More significantly, it requires the bitString to be padded with n zero bits.
The first problem can be solved by testing the coefficient of the remainderPolynomial before it is multiplied by .
The second problem could be solved by doing the last n iterations differently, but there is a more subtle optimization which is used universally, in both hardware and software implementations.
Because the XOR operation used to subtract the generator polynomial from the message is commutative and associative, it does not matter in what order the various inputs are combined into the remainderPolynomial. And specifically, a given bit of the bitString does not need to be added to the remainderPolynomial until the very last instant when it is tested to determine whether to xor with the generatorPolynomial.
This eliminates the need to preload the remainderPolynomial with the first n bits of the message, as well:
function crc(bit array bitString, int len) {
remainderPolynomial := 0
// A popular variant complements remainderPolynomial here; see § Preset to −1 below
for i from 1 to len {
remainderPolynomial := remainderPolynomial xor (bitstring * x)
if (coefficient of x of remainderPolynomial) = 1 {
remainderPolynomial := (remainderPolynomial * x) xor generatorPolynomial
} else {
remainderPolynomial := (remainderPolynomial * x)
}
}
// A popular variant complements remainderPolynomial here; see § Post-invert below
return remainderPolynomial
}
- Code fragment 2: Polynomial division with deferred message XORing
This is the standard bit-at-a-time hardware CRC implementation, and is well worthy of study; once you understand why this computes exactly the same result as the first version, the remaining optimizations are quite straightforward. If remainderPolynomial is only n bits long, then the coefficients of it and of generatorPolynomial are simply discarded. This is the reason that you will usually see CRC polynomials written in binary with the leading coefficient omitted.
In software, it is convenient to note that while one may delay the xor of each bit until the very last moment, it is also possible to do it earlier. It is usually convenient to perform the xor a byte at a time, even in a bit-at-a-time implementation. Here, we take the input in 8-bit bytes:
function crc(byte array string, int len) {
remainderPolynomial := 0
// A popular variant complements remainderPolynomial here; see § Preset to −1 below
for i from 1 to len {
remainderPolynomial := remainderPolynomial xor polynomialForm(string) * x
for j from 1 to 8 { // Assuming 8 bits per byte
if coefficient of x of remainderPolynomial = 1 {
remainderPolynomial := (remainderPolynomial * x) xor generatorPolynomial
} else {
remainderPolynomial := (remainderPolynomial * x)
}
}
}
// A popular variant complements remainderPolynomial here; see § Post-invert below
return remainderPolynomial
}
- Code fragment 3: Polynomial division with bytewise message XORing
This is usually the most compact software implementation, used in microcontrollers when space is at a premium over speed.
Bit ordering (endianness)
When implemented in bit serial hardware, the generator polynomial uniquely describes the bit assignment; the first bit transmitted is always the coefficient of the highest power of , and the last bits transmitted are the CRC remainder , starting with the coefficient of and ending with the coefficient of , a.k.a. the coefficient of 1.
However, when bits are processed a byte at a time, such as when using parallel transmission, byte framing as in 8B/10B encoding or RS-232-style asynchronous serial communication, or when implementing a CRC in software, it is necessary to specify the bit ordering (endianness) of the data; which bit in each byte is considered "first" and will be the coefficient of the higher power of .
If the data is destined for serial communication, it is best to use the bit ordering the data will ultimately be sent in. This is because a CRC's ability to detect burst errors is based on proximity in the message polynomial ; if adjacent polynomial terms are not transmitted sequentially, a physical error burst of one length may be seen as a longer burst due to the rearrangement of bits.
For example, both IEEE 802 (ethernet) and RS-232 (serial port) standards specify least-significant bit first (little-endian) transmission, so a software CRC implementation to protect data sent across such a link should map the least significant bits in each byte to coefficients of the highest powers of . On the other hand, floppy disks and most hard drives write the most significant bit of each byte first.
The lsbit-first CRC is slightly simpler to implement in software, so is somewhat more commonly seen, but many programmers find the msbit-first bit ordering easier to follow. Thus, for example, the XMODEM-CRC extension, an early use of CRCs in software, uses an msbit-first CRC.
So far, the pseudocode has avoided specifying the ordering of bits within bytes by describing shifts in the pseudocode as multiplications by and writing explicit conversions from binary to polynomial form. In practice, the CRC is held in a standard binary register using a particular bit-ordering convention. In msbit-first form, the most significant binary bits will be sent first and so contain the higher-order polynomial coefficients, while in lsbit-first form, the least-significant binary bits contain the higher-order coefficients. The above pseudocode can be written in both forms. For concreteness, this uses the 16-bit CRC-16-CCITT polynomial :
// Most significant bit first (big-endian)
// (x)+x+x+1 = (1) 0001 0000 0010 0001 = 0x1021
function crc(byte array string, int len) {
rem := 0
// A popular variant complements rem here
for i from 1 to len {
rem := rem xor (string leftShift (n-8)) // n = 16 in this example
for j from 1 to 8 { // Assuming 8 bits per byte
if rem and 0x8000 { // Test x coefficient
rem := (rem leftShift 1) xor 0x1021
} else {
rem := rem leftShift 1
}
rem := rem and 0xffff // Trim remainder to 16 bits
}
}
// A popular variant complements rem here
return rem
}
- Code fragment 4: Shift register based division, MSB first
// Least significant bit first (little-endian)
// 1+x+x+(x) = 1000 0100 0000 1000 (1) = 0x8408
function crc(byte array string, int len) {
rem := 0
// A popular variant complements rem here
for i from 1 to len {
rem := rem xor string
for j from 1 to 8 { // Assuming 8 bits per byte
if rem and 0x0001 { // Test x coefficient
rem := (rem rightShift 1) xor 0x8408
} else {
rem := rem rightShift 1
}
}
}
// A popular variant complements rem here
return rem
}
- Code fragment 5: Shift register based division, LSB first
Note that the lsbit-first form avoids the need to shift string before the xor. In either case, be sure to transmit the bytes of the CRC in the order that matches your chosen bit-ordering convention.
Multi-bit computation using lookup tables
Faster software implementations process more than one bit of dividend per iteration using lookup tables, indexed by highest order coefficients of rem, to memoize the per-bit division steps.
Sarwate algorithm (single lookup table)
The most common technique uses a 256-entry lookup table, to process 8 bits of input per iteration. This replaces the body of the outer loop (over i) with:
// Msbit-first rem = (rem leftShift 8) xor big_endian_table xor ((leftmost 8 bits of rem) rightShift (n-8))] // Lsbit-first rem = (rem rightShift 8) xor little_endian_table xor (rightmost 8 bits of rem)]
- Code fragment 6: Cores of table based division
Using a 256-entry table is usually most convenient, but other sizes can be used. In small microcontrollers, using a 16-entry table to process four bits at a time gives a useful speed improvement while keeping the table small. On computers with ample storage, a 65536-entry table can be used to process 16 bits at a time.
Generating the lookup table
The software to generate the lookup table is so small and fast that it is usually faster to compute them on program startup than to load precomputed tables from storage. One popular technique is to use the bit-at-a-time code 256 times to generate the CRCs of the 256 possible 8-bit bytes. However, this can be optimized significantly by taking advantage of the property that table == table xor table. Only the table entries corresponding to powers of two need to be computed directly.
In the following example code, crc holds the value of table:
big_endian_table := 0
crc := 0x8000 // Assuming a 16-bit polynomial
i := 1
do {
if crc and 0x8000 {
crc := (crc leftShift 1) xor 0x1021 // The CRC polynomial
} else {
crc := crc leftShift 1
}
// crc is the value of big_endian_table; let j iterate over the already-initialized entries
for j from 0 to i−1 {
big_endian_table := crc xor big_endian_table;
}
i := i leftshift 1
} while i < 256
- Code fragment 7: Byte-at-a-time CRC table generation, msbit-first
little_endian_table := 0
crc := 1;
i := 128
do {
if crc and 1 {
crc := (crc rightShift 1) xor 0x8408 // The CRC polynomial
} else {
crc := crc rightShift 1
}
// crc is the value of little_endian_table; let j iterate over the already-initialized entries
for j from 0 to 255 by 2 × i {
little_endian_table := crc xor little_endian_table;
}
i := i rightshift 1
} while i > 0
- Code fragment 8: Byte-at-a-time CRC table generation, lsbit-first
In these code samples, the table index i + j is equivalent to i xor j; you may use whichever form is more convenient.
CRC-32 example
One of the most commonly encountered CRC polynomials is known as CRC-32, used by (among others) Ethernet, FDDI, ZIP and other archive formats, and PNG image format. Its polynomial can be written msbit-first as 0x04C11DB7, or lsbit-first as 0xEDB88320.
This is a practical example for the CRC-32 variant of CRC.
An alternate source is the W3C webpage on PNG, which includes an appendix with a short and simple table-driven implementation in C of CRC-32. You will note that the code corresponds to the lsbit-first byte-at-a-time algorithm presented here, and the table is generated using the bit-at-a-time code.
Function CRC32
Input:
data: Bytes // Array of bytes
Output:
crc32: UInt32 // 32-bit unsigned CRC-32 value
// Initialize CRC-32 to starting value
crc32 ← 0xFFFFFFFF
for each byte in data do
nLookupIndex ← (crc32 xor byte) and 0xFF
crc32 ← (crc32 shr 8) xor CRCTable // CRCTable is an array of 256 32-bit constants
// Finalize the CRC-32 value by inverting all the bits
crc32 ← crc32 xor 0xFFFFFFFF
return crc32
In C, the algorithm looks like:
#include <stdint.h> // uint32_t, uint8_t
static uint32_t CRCTable;
// Initialization by multiple threads is redundant, but safe.
static void CRC32_init(void)
{
uint32_t crc32 = 1;
// C guarantees CRCTable = 0 already.
for (unsigned int i = 128; i; i >>= 1) {
crc32 = (crc32 >> 1) ^ (crc & 1 ? 0xedb88320 : 0);
for (unsigned int j = 0; j < 256; j += 2*i)
CRCTable = crc32 ^ CRCTable;
}
}
uint32_t CRC32(const uint8_t data, size_t data_length)
{
uint32_t crc32 = 0xFFFFFFFFu;
if (crcTable == 0)
CRC32_init();
for (size_t i = 0; i < data_length; i++) {
crc32 ^= data;
crc32 = (crc32 >> 8) ^ CRCTable;
}
// Finalize the CRC-32 value by inverting all the bits
crc32 ^= 0xFFFFFFFFu;
return crc32;
}
Byte-Slicing using multiple tables
There exists a slice-by-n (typically slice-by-8 for CRC32) algorithm that usually doubles or triples the performance compared to the Sarwate algorithm. Instead of reading 8 bits at a time, the algorithm reads 8n bits at a time. Doing so maximizes performance on superscalar processors.
It is unclear who actually invented the algorithm.
To understand the advantages, start with the slice-by-2 case. We wish to compute a CRC two bytes (16 bits) at a time, but the standard table-based approach would require an inconveniently large 65536-entry table. As mentioned in § Generating the lookup table, CRC tables have the property that table = table xor table. We can use this identity to replace the large table by two 256-entry tables: table = table_low xor table_high.
So the large table is not stored explicitly, but each iteration computes the CRC value that would be there by combining the values in two smaller tables. That is, the 16-bit index is "sliced" into two 8-bit indexes. At first glance, this seems pointless; why do two lookups in separate tables, when the standard byte-at-a-time algorithm would do two lookups in the same table?
The difference is instruction-level parallelism. In the standard algorithm, the index for each lookup depends on the value fetched in the previous one. Thus, the second lookup cannot begin until the first lookup is complete.
When sliced tables are used, both lookups can begin at the same time. If the processor can perform two loads in parallel (2020s microprocessors can keep track of over 100 loads in progress), then this has the potential to double the speed of the inner loop.
This technique can obviously be extended to as many slices as the processor can benefit from.
When the slicing width equals the CRC size, there is a minor speedup. In the part of the basic Sarwate algorithm where the previous CRC value is shifted by the size of the table lookup, the previous CRC value is shifted away entirely (what remains is all zero), so the XOR can be eliminated from the critical path.
The resultant slice-by-n inner loop consists of:
- XOR the current CRC with the next n bytes of the message,
- look up each byte of the resultant value in the n slice tables, then
- XOR the n results to get the next CRC.
This still has the property that all of the loads in the second step must be completed before the next iteration can commence, resulting in regular pauses during which the processor's memory subsystem (in particular, the data cache) is unused. However, when the slicing width exceeds the CRC size, a significant second speedup appears.
This is because a portion of the results of the first step no longer depend on any previous iteration. When XORing a 32-bit CRC with 64 bits of message, half of the result is simply a copy of the message. If coded carefully (to avoid creating a false data dependency), half of the slice table loads can begin before the previous loop iteration has completed. The result is enough work to keep the processor's memory subsystem continuously busy, which achieves maximum performance. As mentioned, on post-2000 microprocessors, slice-by-8 is generally sufficient to reach this level.
There is no particular need for the slices to be 8 bits wide. For example, it would be entirely possible to compute a CRC 64 bits at a time using a slice-by-9 algorithm, using 9 128-entry lookup tables to handle 63 bits, and the 64th bit handled by the bit-at-a-time algorithm (which is effectively a 1-bit, 2-entry lookup table). This would almost halve the table size (going from 8×256 = 2048 entries to 9×128 = 1152) at the expense of one more data-dependent load per iteration.
Generating the tables
The tables for slicing computation are a simple extension of the table for the basic Sarwate algorithm. The loop for the 256 entries of each table is identical, but beginning with the crc value left over from the previous table.
Multi-bit computation without lookup tables
Parallel update for a byte or a word at a time can also be done explicitly, without a table. For each bit an equation is solved after 8 bits have been shifted in.
Multiple reduction steps are normally expressed as a matrix operation. One shift and reduction modulo a degree- generator polynomial is equivalent to multiplication by the companion matrix . steps are written as the matrix .
This technique is normally used in high-speed hardware implementations, but is practical in software for small or sparse CRC polynomials. For large, dense CRC polynomials, the code becomes impractically long.
Examples for sparse polynomials
The following tables list the equations processing 8 bits at a time modulo some commonly used polynomials, using the following symbols:
| ci | CRC bit 7…0 (or 15…0) before update |
| ri | CRC bit 7…0 (or 15…0) after update |
| di | input data bit 7…0 |
| ei = di + ci | ep = e7 + e6 + … + e1 + e0 (parity bit) |
| si = di + ci+8 | sp = s7 + s6 + … + s1 + s0 (parity bit) |
| Polynomial: | x(x + x + 1) (left-shifted CRC-7-CCITT) | x + x + x + 1 (CRC-8-Dallas/Maxim) |
|---|---|---|
| Coefficients: | 0x12 = (0x09 << 1) (msbit-first) | 0x8c (lsbit-first) |
r0 ← r1 ← r2 ← r3 ← r4 ← r5 ← r6 ← r7 ← |
0 e0 + e4 + e7 e1 + e5 e2 + e6 e3 + e7 + e0 + e4 + e7 e4 + e1 + e5 e5 + e2 + e6 e6 + e3 + e7 |
e0 + e4 + e1 + e0 + e5 + e2 + e1 e1 + e5 + e2 + e1 + e6 + e3 + e2 + e0 e2 + e6 + e3 + e2 + e0 + e7 + e4 + e3 + e1 e3 + e0 + e7 + e4 + e3 + e1 e4 + e1 + e0 e5 + e2 + e1 e6 + e3 + e2 + e0 e7 + e4 + e3 + e1 |
| C code fragments: |
uint8_t c, d, e, f, r; … e = c ^ d; f = e ^ (e >> 4) ^ (e >> 7); r = (f << 1) ^ (f << 4); |
uint8_t c, d, e, f, r; … e = c ^ d; f = e ^ (e << 3) ^ (e << 4) ^ (e << 6); r = f ^ (f >> 4) ^ (f >> 5); |
| Polynomial: | x + x + x + 1 (CRC-16-CCITT) | |
|---|---|---|
| Coefficients: | 0x1021 (msbit-first) | 0x8408 (lsbit-first) |
r0 ← r1 ← r2 ← r3 ← r4 ← r5 ← r6 ← r7 ← r8 ← r9 ← r10 ← r11 ← r12 ← r13 ← r14 ← r15 ← |
s4 + s0
s5 + s1
s6 + s2
s7 + s3
s4
s5 + s4 + s0
s6 + s5 + s1
s7 + s6 + s2
c0 + s7 + s3
c1 + s4
c2 + s5
c3 + s6
c4 + s7 + s4 + s0
c5 + s5 + s1
c6 + s6 + s2
c7 + s7 + s3
|
c8 + e4 + e0 c9 + e5 + e1 c10 + e6 + e2 c11 + e0 + e7 + e3 c12 + e1 c13 + e2 c14 + e3 c15 + e4 + e0 e0 + e5 + e1 e1 + e6 + e2 e2 + e7 + e3 e3 e4 + e0 e5 + e1 e6 + e2 e7 + e3 |
| C code fragments: |
uint8_t d, s, t;
uint16_t c, r;
…
s = d ^ (c >> 8);
t = s ^ (s >> 4);
r = (c << 8) ^
t ^
(t << 5) ^
(t << 12);
|
uint8_t d, e, f;
uint16_t c, r;
…
e = c ^ d;
f = e ^ (e << 4);
r = (c >> 8) ^
(f << 8) ^
(f << 3) ^
(f >> 4);
|
| Polynomial: | x + x + x + 1 (CRC-16-ANSI) | |
|---|---|---|
| Coefficients: | 0x8005 (MSBF/normal) | 0xa001 (LSBF/reverse) |
r0 ← r1 ← r2 ← r3 ← r4 ← r5 ← r6 ← r7 ← r8 ← r9 ← r10 ← r11 ← r12 ← r13 ← r14 ← r15 ← |
sp
s0 + sp
s1 + s0
s2 + s1
s3 + s2
s4 + s3
s5 + s4
s6 + s5
c0 + s7 + s6
c1 + s7
c2
c3
c4
c5
c6
c7 + sp
|
c8 + ep
c9
c10
c11
c12
c13
c14 + e0
c15 + e1 + e0
e2 + e1
e3 + e2
e4 + e3
e5 + e4
e6 + e5
e7 + e6
ep + e7
ep
|
| C code fragments: |
uint8_t d, s, p;
uint16_t c, r, t;
…
s = d ^ (c >> 8);
p = s ^ (s >> 4);
p = p ^ (p >> 2);
p = p ^ (p >> 1);
p = p & 1;
t = p | (s << 1);
r = (c << 8) ^
(t << 15) ^
t ^
(t << 1);
|
uint8_t d, e, p;
uint16_t c, r, f;
…
e = c ^ d;
p = e ^ (e >> 4);
p = p ^ (p >> 2);
p = p ^ (p >> 1);
p = p & 1;
f = e | (p << 8);
r = (c >> 8) ^
(f << 6) ^
(f << 7) ^
(f >> 8);
|
Two-step computation
For dense polynomials, such as the CRC-32 polynomial, computing the remainder a byte at a time produces equations where each bit depends on up to 8 bits of the previous iteration. In byte-parallel hardware implementations this calls for either 8-input or cascaded XOR gates which have substantial gate delay.
To maximise computation speed, an intermediate remainder can be calculated by first computing the CRC of the message modulo a sparse polynomial which is a multiple of the CRC polynomial. For CRC-32, the polynomial x + x + x + x + x + x + x + 1 has the property that its terms (feedback taps) are at least 8 positions apart. Thus, a 123-bit shift register can be advanced 8 bits per iteration using only two-input XOR gates, the fastest possible. Finally the intermediate remainder can be reduced modulo the standard polynomial in a second slower shift register (once per CRC, rather than once per input byte) to yield the CRC-32 remainder.
If 3- or 4-input XOR gates are permitted, shorter intermediate polynomials of degree 71 or 53, respectively, can be used.
State-space transformation
The preceding technique works, but requires a large intermediate shift register. A more hardware-efficient technique which has been used for high-speed networking since c. 2000 is state-space transformation. The inner loop of a -bit-at-a-time CRC engine is to repeatedly update the intermediate remainder to reflect an -bit portion of the message using:
The implementation challenge is that the matrix multiplication by must be performed in bit times. In general, as increases, the so does the complexity of this multiplication, resulting in a maximum speedup of about TO improve on this, first break this up the equation using distributivity into:
Then, we find an invertible matrix and perform a change of basis, multipling the intermediate state by . So the iteration becomes:
The final CRC is recovered as It's important to note that the input multiplication by and the output multiplication by are not time-critical, as they can be pipelined to whatever depth is required to meet the performance target. Only the central multiplication by must be completed within bit times. Techniques has been developed for finding a transformation matrix which gives that the form of a companion matrix. In other words, it can be implemented using the same (fast) 2-input XOR gates as the bit-at-a-time algorithm. This allows an -bit parallel CRC to operate times as fast as a 1-bit serial implementation.
There are many possible transformation matrices with this property, so it is possible to choose one which also minimizes the complexity of the input and output matrices and .
Block-wise computation
| This section may be confusing or unclear to readers. In particular, the explanation isn't detailed enough to understand without the referenced source, and it's buried behind a paywall, leaving the reader stranded.. Please help clarify the section. There might be a discussion about this on the talk page. (January 2025) (Learn how and when to remove this message) |
Block-wise computation of the remainder can be performed in hardware for any CRC polynomial by factorizing the state space transformation matrix needed to compute the remainder into two simpler Toeplitz matrices.
One-pass checking
When appending a CRC to a message, it is possible to detach the transmitted CRC, recompute it, and verify the recomputed value against the transmitted one. However, a simpler technique is commonly used in hardware.
When the CRC is transmitted with the correct byte order (matching the chosen bit-ordering convention), a receiver can compute an overall CRC, over the message and the CRC, and if they are correct, the result will be zero. This possibility is the reason that most network protocols which include a CRC do so before the ending delimiter; it is not necessary to know whether the end of the packet is imminent to check the CRC.
In fact, a few protocols use the CRC as the message delimiter, a technique called CRC-based framing. (This requires multiple frames to detect acquisition or loss of framing, so is limited to applications where the frames are a known length, and the frame contents are sufficiently random that valid CRCs in misaligned data are rare.)
CRC variants
In practice, most standards specify presetting the register to all-ones and inverting the CRC before transmission. This has no effect on the ability of a CRC to detect changed bits, but gives it the ability to notice bits that are added to the message.
Preset to −1
The basic mathematics of a CRC accepts (considers as correctly transmitted) messages which, when interpreted as a polynomial, are a multiple of the CRC polynomial. If some leading 0 bits are prepended to such a message, they will not change its interpretation as a polynomial. This is equivalent to the fact that 0001 and 1 are the same number.
But if the message being transmitted does care about leading 0 bits, the inability of the basic CRC algorithm to detect such a change is undesirable. If it is possible that a transmission error could add such bits, a simple solution is to start with the rem shift register set to some non-zero value; for convenience, the all-ones value is typically used. This is mathematically equivalent to complementing (binary NOT) the first n bits of the message, where n is the number of bits in the CRC register.
This does not affect CRC generation and checking in any way, as long as both generator and checker use the same initial value. Any non-zero initial value will do, and a few standards specify unusual values, but the all-ones value (−1 in twos complement binary) is by far the most common. Note that a one-pass CRC generate/check will still produce a result of zero when the message is correct, regardless of the preset value.
Post-invert
The same sort of error can occur at the end of a message, albeit with a more limited set of messages. Appending 0 bits to a message is equivalent to multiplying its polynomial by x, and if it was previously a multiple of the CRC polynomial, the result of that multiplication will be, as well. This is equivalent to the fact that, since 726 is a multiple of 11, so is 7260.
A similar solution can be applied at the end of the message, inverting the CRC register before it is appended to the message. Again, any non-zero change will do; inverting all the bits (XORing with an all-ones pattern) is simply the most common.
This has an effect on one-pass CRC checking: instead of producing a result of zero when the message is correct, it produces a fixed non-zero result. (To be precise, the result is the CRC, with zero preset but with post-invert, of the inversion pattern.) Once this constant has been obtained (e.g. by performing a one-pass CRC generate/check on an arbitrary message), it can be used directly to verify the correctness of any other message checked using the same CRC algorithm.
See also
General category
- Error correction code
- List of hash functions
- Parity is equivalent to a 1-bit CRC with polynomial x+1.
Non-CRC checksums
References
- Dubrova, Elena; Mansouri, Shohreh Sharif (May 2012). "A BDD-Based Approach to Constructing LFSRS for Parallel CRC Encoding". 2012 IEEE 42nd International Symposium on Multiple-Valued Logic. pp. 128–133. doi:10.1109/ISMVL.2012.20. ISBN 978-0-7695-4673-5. S2CID 27306826.
- ^ Williams, Ross N. (1996-09-24). "A Painless Guide to CRC Error Detection Algorithms V3.00". Archived from the original on 2006-09-27. Retrieved 2016-02-16.
- Sarwate, Dilip V. (August 1998). "Computation of Cyclic Redundancy Checks via Table Look-Up". Communications of the ACM. 31 (8): 1008–1013. doi:10.1145/63030.63037. S2CID 5363350.
- ^ "Portable Network Graphics (PNG) Specification (Second Edition): Annex D, Sample Cyclic Redundancy Code implementation". W3C. 2003-11-10. Retrieved 2016-02-16.
- "[MS-ABS]: 32-Bit CRC Algorithm". msdn.microsoft.com. Archived from the original on 7 November 2017. Retrieved 4 November 2017.
- Kounavis, M.E.; Berry, F.L. (2005). "A Systematic Approach to Building High Performance Software-Based CRC Generators". 10th IEEE Symposium on Computers and Communications (ISCC'05) (PDF). pp. 855–862. doi:10.1109/ISCC.2005.18. ISBN 0-7695-2373-0. S2CID 10308354.
- Berry, Frank L.; Kounavis, Michael E. (November 2008). "Novel Table Lookup-Based Algorithms for High-Performance CRC Generation". IEEE Transactions on Computers. 57 (11): 1550–1560. doi:10.1109/TC.2008.85. S2CID 206624854.
- High Octane CRC Generation with the Intel Slicing-by-8 Algorithm (PDF) (Technical report). Intel. Archived from the original (PDF) on 2012-07-22.
- "Brief tutorial on CRC computation". The Linux Kernel Archives.
- Menon-Sen, Abhijit (2017-01-20). "Who invented the slicing-by-N CRC32 algorithm?".
- Jon Buller (1996-03-15). "Re: 8051 and CRC-CCITT". Newsgroup: comp.arch.embedded. Usenet: 31498ED0.7C0A@nortel.com. Retrieved 2016-02-16.
- AVR-LibC project (15 March 2024). "AVR-LibC <util/crc16.h>".
- Glaise, René J. (1997-01-20). "A two-step computation of cyclic redundancy code CRC-32 for ATM networks". IBM Journal of Research and Development. 41 (6). Armonk, NY: IBM: 705. doi:10.1147/rd.416.0705. Archived from the original on 2009-01-30. Retrieved 2016-02-16.
- Derby, Jeff H. (25–29 November 2001). High-speed CRC computation using state-space transformations. Global Telecommunications Conference. San Antonio, TX, USA. pp. 166–170. doi:10.1109/GLOCOM.2001.965100.
- ^ Kennedy, Christopher; Reyhani-Masoleh, Arash (7 June 2009). High-speed CRC computations using improved state-space transformations. IEEE International Conference on Electro/Information Technology. doi:10.1109/EIT.2009.5189575.
- Das, Arindam (April 2023). "Block-wise computation of Cyclic Redundancy Code using factored Toeplitz matrices in lieu of Look-Up Table". IEEE Transactions on Computers. 72 (4): 1110–1121. doi:10.1109/TC.2022.3189574. ISSN 0018-9340. S2CID 250472783.
- Kadatch, Andrew; Jenkins, Bob (3 September 2010). Everything we know about CRC but afraid to forget (PDF) (Technical report). p. 4.
The fact that the CRC of a message followed by its CRC is a constant value which does not depend on the message... is well known and has been widely used in the telecommunication industry for long time.
{{cite tech report}}: CS1 maint: year (link) A good source for even more - E.g. low-frequency RFID TMS37157 data sheet - Passive Low Frequency Interface Device With EEPROM and 134.2 kHz Transponder Interface (PDF), Texas Instruments, November 2009, p. 39, retrieved 2016-02-16,
The CRC Generator is initialized with the value 0x3791 as shown in Figure 50.
External links
- JohnPaul Adamovsky. "64 Bit Cyclic Redundant Code – XOR Long Division To Bytewise Table Lookup".
- Andrew Kadarch, Bob Jenkins. "Efficient (~1 CPU cycle per byte) CRC implementation". GitHub.
 . Writing the first bit transmitted (the coefficient of the highest power of
. Writing the first bit transmitted (the coefficient of the highest power of  ) on the left, this corresponds to the 9-bit string "100000111".
) on the left, this corresponds to the 9-bit string "100000111".
 . Msbit-first, this is
. Msbit-first, this is  = 01010111, while lsbit-first, it is
= 01010111, while lsbit-first, it is  = 11101010. These can then be multiplied by
= 11101010. These can then be multiplied by  to produce two 16-bit message polynomials
to produce two 16-bit message polynomials  .
.
 . This is just like decimal long division, but even simpler because the only possible multiples at each step are 0 and 1, and the subtractions
. This is just like decimal long division, but even simpler because the only possible multiples at each step are 0 and 1, and the subtractions  . Converting to a hexadecimal number using the convention that the highest power of x is the msbit; this is A216. In the lsbit-first, the remainder is
. Converting to a hexadecimal number using the convention that the highest power of x is the msbit; this is A216. In the lsbit-first, the remainder is  . Converting to hexadecimal using the convention that the highest power of x is the lsbit, this is 1916.
. Converting to hexadecimal using the convention that the highest power of x is the lsbit, this is 1916.
 -bit
-bit  coefficient, which could be the right or left end of the register.
coefficient, which could be the right or left end of the register.
 coefficient can be tested. More significantly, it requires the
coefficient can be tested. More significantly, it requires the  coefficient of the
coefficient of the  , starting with the coefficient of
, starting with the coefficient of  :
:

 .
.  steps are written as the matrix
steps are written as the matrix  .
.
 to reflect an
to reflect an  using:
using:

 must be performed in
must be performed in  TO improve on this, first break this up the equation using
TO improve on this, first break this up the equation using 
 and perform a
and perform a  . So the iteration becomes:
. So the iteration becomes:

 It's important to note that the input multiplication by
It's important to note that the input multiplication by  and the output multiplication by
and the output multiplication by  must be completed within
must be completed within