In geometry, two diameters of a conic section are said to be conjugate if each chord parallel to one diameter is bisected by the other diameter. For example, two diameters of a circle are conjugate if and only if they are perpendicular.
Of ellipse

For an ellipse, two diameters are conjugate if and only if the tangent line to the ellipse at an endpoint of one diameter is parallel to the other diameter. Each pair of conjugate diameters of an ellipse has a corresponding tangent parallelogram, sometimes called a bounding parallelogram (skewed compared to a bounding rectangle). In his manuscript De motu corporum in gyrum, and in the 'Principia', Isaac Newton cites as a lemma proved by previous authors that all (bounding) parallelograms for a given ellipse have the same area.
It is possible to reconstruct an ellipse from any pair of conjugate diameters, or from any bounding parallelogram. For example, in proposition 14 of Book VIII of his Collection, Pappus of Alexandria gives a method for constructing the axes of an ellipse from a given pair of conjugate diameters. Another method is using Rytz's construction, which takes advantage of the Thales' theorem for finding the directions and lengths of the major and minor axes of an ellipse regardless of its rotation or shearing.
In analytic geometry, if we let the vectors of the two conjugate half-diameters be , then the ellipse is parameterized by as varies over .
Of hyperbola
Similar to the elliptic case, diameters of a hyperbola are conjugate when each bisects all chords parallel to the other. In this case both the hyperbola and its conjugate are sources for the chords and diameters.
Apollonius of Perga gave the following construction of conjugate diameters, given the conjugate hyperbola: "If Q be any point on a hyperbola and CE be drawn from the centre parallel to the tangent at Q to meet the conjugate hyperbola in E, then (1) the tangent at E will be parallel to CQ and (2) CQ and CE will be conjugate diameters."
In analytic geometry, if are vectors of the two conjugate half-diameters, then the hyperbola is parameterized by as varies over .
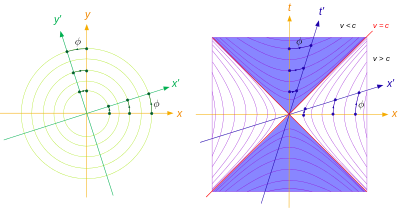
In the case of a rectangular hyperbola, its conjugate is the reflection across an asymptote. A diameter of one hyperbola is conjugate to its reflection in the asymptote, which is a diameter of the other hyperbola. As perpendicularity is the relation of conjugate diameters of a circle, so hyperbolic orthogonality is the relation of conjugate diameters of rectangular hyperbolas.
The placement of tie rods reinforcing a square assembly of girders is guided by the relation of conjugate diameters in a book on analytic geometry.
Conjugate diameters of hyperbolas are also useful for stating the principle of relativity in the modern physics of spacetime. The concept of relativity is first introduced in a plane consisting of a single dimension in space, the second dimension being time. In such a plane, one hyperbola corresponds to events a constant space-like interval from the origin event, the other hyperbola corresponds to events a constant time-like interval from it. The principle of relativity can be formulated "Any pair of conjugate diameters of conjugate hyperbolas can be taken for the axes of space and time". This interpretation of relativity was enunciated by E. T. Whittaker in 1910.
In projective geometry
Every line in projective geometry contains a point at infinity, also called a figurative point. The ellipse, parabola, and hyperbola are viewed as conics in projective geometry, and each conic determines a relation of pole and polar between points and lines. Using these concepts, "two diameters are conjugate when each is the polar of the figurative point of the other."
Only one of the conjugate diameters of a hyperbola cuts the curve.
The notion of point-pair separation distinguishes an ellipse from a hyperbola: In the ellipse every pair of conjugate diameters separates every other pair. In a hyperbola, one pair of conjugate diameters never separates another such pair.
References
- Spain, Barry (1957). Analytical Conics. International series of monographs in pure and applied mathematics.v.3. New York: Pergamon Press. p. 49.
- Thomas Heath (1896) Apollonius of Perga: Treatise on Conic Sections, page 64
- Osgood, William F.; Graustein, William C. (1921). Plane and solid analytic geometry. New York: The Macmillan Company. p. 307.
- Whittaker, E.T. (1910). A History of the Theories of Aether and Electricity (1 ed.). Dublin: Longman, Green and Co. p. 441.
- G. B. Halsted (1906) Synthetic Projective Geometry, #135, #141
Further reading
- Chasles, Michel (1865). "Diamètres conjugués". Traité des sections coniques, Ie partie. faisant suite au traité de géométrie supérieure (in French). Paris: Gauthier-Villars. pp. 116–23.
- W. K. Clifford (1878) Elements of Dynamic, page 90, link from HathiTrust.
- Coxeter, HSM (1955). The Real Projective Plane (2nd ed.). Cambridge University Press. pp. 130–5.
- Salmon, George (1900). A Treatise on Conic Sections. London: Longmans, Green & Co. p. 165.
External links
- "Conjugate Diameters in Ellipse". cut-the-knot.org.
- Besant, W. H. (1895). "Properties of Conjugate Diameters". Conic sections treated geometrically. Historical Math Monographs. London; Ithaca, NY: G. Bell; Cornell University. p. 109.
 , then the ellipse is parameterized by
, then the ellipse is parameterized by  as
as  varies over
varies over  .
.
 are vectors of the two conjugate half-diameters, then the hyperbola is parameterized by
are vectors of the two conjugate half-diameters, then the hyperbola is parameterized by  as
as  .
.