| This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Current source" – news · newspapers · books · scholar · JSTOR (January 2019) (Learn how and when to remove this message) |
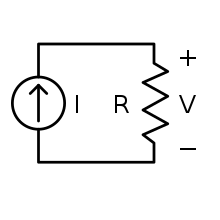
A current source is an electronic circuit that delivers or absorbs an electric current which is independent of the voltage across it.
A current source is the dual of a voltage source. The term current sink is sometimes used for sources fed from a negative voltage supply. Figure 1 shows the schematic symbol for an ideal current source driving a resistive load. There are two types. An independent current source (or sink) delivers a constant current. A dependent current source delivers a current which is proportional to some other voltage or current in the circuit.
Background
|

|
| Voltage source | Current source |
|
|
| Controlled voltage source | Controlled current source |
| Battery of cells | Single cell |
An ideal current source generates a current that is independent of the voltage changes across it. An ideal current source is a mathematical model, which real devices can approach very closely. If the current through an ideal current source can be specified independently of any other variable in a circuit, it is called an independent current source. Conversely, if the current through an ideal current source is determined by some other voltage or current in a circuit, it is called a dependent or controlled current source. Symbols for these sources are shown in Figure 2.
The internal resistance of an ideal current source is infinite. An independent current source with zero current is identical to an ideal open circuit. The voltage across an ideal current source is completely determined by the circuit it is connected to. When connected to a short circuit, there is zero voltage and thus zero power delivered. When connected to a load resistance, the current source manages the voltage in such a way as to keep the current constant; so in an ideal current source the voltage across the source approaches infinity as the load resistance approaches infinity (an open circuit).
No physical current source is ideal. For example, no physical current source can operate when applied to an open circuit. There are two characteristics that define a current source in real life. One is its internal resistance and the other is its compliance voltage. The compliance voltage is the maximum voltage that the current source can supply to a load. Over a given load range, it is possible for some types of real current sources to exhibit nearly infinite internal resistance. However, when the current source reaches its compliance voltage, it abruptly stops being a current source.
In circuit analysis, a current source having finite internal resistance is modeled by placing the value of that resistance across an ideal current source (the Norton equivalent circuit). However, this model is only useful when a current source is operating within its compliance voltage.
Implementations
Passive current source
The simplest non-ideal current source consists of a voltage source in series with a resistor. The amount of current available from such a source is given by the ratio of the voltage across the voltage source to the resistance of the resistor (Ohm's law; I = V/R). This value of current will only be delivered to a load with zero voltage drop across its terminals (a short circuit, an uncharged capacitor, a charged inductor, a virtual ground circuit, etc.) The current delivered to a load with nonzero voltage (drop) across its terminals (a linear or nonlinear resistor with a finite resistance, a charged capacitor, an uncharged inductor, a voltage source, etc.) will always be different. It is given by the ratio of the voltage drop across the resistor (the difference between the exciting voltage and the voltage across the load) to its resistance.
For a nearly ideal current source, the value of the resistor should be very large but this implies that, for a specified current, the voltage source must be very large (in the limit as the resistance and the voltage go to infinity, the current source will become ideal and the current will not depend at all on the voltage across the load). Thus, efficiency is low (due to power loss in the resistor) and it is usually impractical to construct a 'good' current source this way. Nonetheless, it is often the case that such a circuit will provide adequate performance when the specified current and load resistance are small. For example, a 5 V voltage source in series with a 4.7 kΩ resistor will provide an approximately constant current of 1 mA ± 5% to a load resistance in the range of 50 to 450 Ω.
A Van de Graaff generator is an example of such a high voltage current source. It behaves as an almost constant current source because of its very high output voltage coupled with its very high output resistance and so it supplies the same few microamperes at any output voltage up to hundreds of thousands of volts (or even tens of megavolts) for large laboratory versions.
Active current sources without negative feedback
In these circuits the output current is not monitored and controlled by means of negative feedback.
Current-stable nonlinear implementation
They are implemented by active electronic components (transistors) having current-stable nonlinear output characteristic when driven by steady input quantity (current or voltage). These circuits behave as dynamic resistors changing their present resistance to compensate current variations. For example, if the load increases its resistance, the transistor decreases its present output resistance (and vice versa) to keep up a constant total resistance in the circuit.
Active current sources have many important applications in electronic circuits. They are often used in place of ohmic resistors in analog integrated circuits (e.g., a differential amplifier) to generate a current that depends slightly on the voltage across the load.
The common emitter configuration driven by a constant input current or voltage and common source (common cathode) driven by a constant voltage naturally behave as current sources (or sinks) because the output impedance of these devices is naturally high. The output part of the simple current mirror is an example of such a current source widely used in integrated circuits. The common base, common gate and common grid configurations can serve as constant current sources as well.
A JFET can be made to act as a current source by tying its gate to its source. The current then flowing is the IDSS of the FET. These can be purchased with this connection already made and in this case the devices are called current regulator diodes or constant current diodes or current limiting diodes (CLD). Alternatively, an enhancement-mode N-channel MOSFET (metal–oxide–semiconductor field-effect transistor) could be used instead of a JFET in the circuits listed below for similar functionality.
Following voltage implementation
An example: bootstrapped current source.
Voltage compensation implementation
The simple resistor passive current source is ideal only when the voltage across it is zero; so voltage compensation by applying parallel negative feedback might be considered to improve the source. Operational amplifiers with feedback effectively work to minimise the voltage across their inputs. This results in making the inverting input a virtual ground, with the current running through the feedback, or load, and the passive current source. The input voltage source, the resistor, and the op-amp constitutes an "ideal" current source with value, IOUT = VIN/R. The transimpedance amplifier and an op-amp inverting amplifier are typical implementations of this idea.
The floating load is a serious disadvantage of this circuit solution.
Current compensation implementation
A typical example are Howland current source and its derivative Deboo integrator. In the last example (Fig. 1), the Howland current source consists of an input voltage source, VIN, a positive resistor, R, a load (the capacitor, C, acting as impedance Z) and a negative impedance converter INIC (R1 = R2 = R3 = R and the op-amp). The input voltage source and the resistor R constitute an imperfect current source passing current, IR through the load (Fig. 3 in the source). The INIC acts as a second current source passing "helping" current, I−R, through the load. As a result, the total current flowing through the load is constant and the circuit impedance seen by the input source is increased. However the Howland current source isn't widely used because it requires the four resistors to be perfectly matched, and its impedance drops at high frequencies.
The grounded load is an advantage of this circuit solution.
Current sources with negative feedback
| This section does not cite any sources. Please help improve this section by adding citations to reliable sources. Unsourced material may be challenged and removed. (October 2014) (Learn how and when to remove this message) |
They are implemented as a voltage follower with series negative feedback driven by a constant input voltage source (i.e., a negative feedback voltage stabilizer). The voltage follower is loaded by a constant (current sensing) resistor acting as a simple current-to-voltage converter connected in the feedback loop. The external load of this current source is connected somewhere in the path of the current supplying the current sensing resistor but out of the feedback loop.
The voltage follower adjusts its output current IOUT flowing through the load so that to make the voltage drop VR = IOUTR across the current sensing resistor R equal to the constant input voltage VIN. Thus the voltage stabilizer keeps up a constant voltage drop across a constant resistor; so, a constant current IOUT = VR/R = VIN/R flows through the resistor and respectively through the load.
If the input voltage varies, this arrangement will act as a voltage-to-current converter (voltage-controlled current source, VCCS); it can be thought as a reversed (by means of negative feedback) current-to-voltage converter. The resistance R determines the transfer ratio (transconductance).
Current sources implemented as circuits with series negative feedback have the disadvantage that the voltage drop across the current sensing resistor decreases the maximal voltage across the load (the compliance voltage).
Simple transistor current sources
Constant current diode
Main article: Constant-current diode
The simplest constant-current source or sink is formed from one component: a JFET with its gate attached to its source. Once the drain-source voltage reaches a certain minimum value, the JFET enters saturation where current is approximately constant. This configuration is known as a constant-current diode, as it behaves much like a dual to the constant voltage diode (Zener diode) used in simple voltage sources.
Due to the large variability in saturation current of JFETs, it is common to also include a source resistor (shown in the adjacent image) which allows the current to be tuned down to a desired value.
Zener diode current source
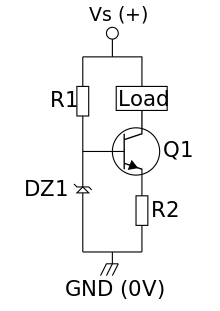
In this bipolar junction transistor (BJT) implementation (Figure 4) of the general idea above, a Zener voltage stabilizer (R1 and DZ1) drives an emitter follower (Q1) loaded by a constant emitter resistor (R2) sensing the load current. The external (floating) load of this current source is connected to the collector so that almost the same current flows through it and the emitter resistor (they can be thought of as connected in series). The transistor, Q1, adjusts the output (collector) current so as to keep the voltage drop across the constant emitter resistor, R2, almost equal to the relatively constant voltage drop across the Zener diode, DZ1. As a result, the output current is almost constant even if the load resistance and/or voltage vary. The operation of the circuit is considered in details below.
A Zener diode, when reverse biased (as shown in the circuit) has a constant voltage drop across it irrespective of the current flowing through it. Thus, as long as the Zener current (IZ) is above a certain level (called holding current), the voltage across the Zener diode (VZ) will be constant. Resistor, R1, supplies the Zener current and the base current (IB) of NPN transistor (Q1). The constant Zener voltage is applied across the base of Q1 and emitter resistor, R2.
Voltage across R2 (VR2) is given by VZ − VBE, where VBE is the base-emitter drop of Q1. The emitter current of Q1 which is also the current through R2 is given by
Since VZ is constant and VBE is also (approximately) constant for a given temperature, it follows that VR2 is constant and hence IE is also constant. Due to transistor action, emitter current, IE, is very nearly equal to the collector current, IC, of the transistor (which in turn, is the current through the load). Thus, the load current is constant (neglecting the output resistance of the transistor due to the Early effect) and the circuit operates as a constant current source. As long as the temperature remains constant (or doesn't vary much), the load current will be independent of the supply voltage, R1 and the transistor's gain. R2 allows the load current to be set at any desirable value and is calculated by
where VBE is typically 0.65 V for a silicon device.
(IR2 is also the emitter current and is assumed to be the same as the collector or required load current, provided hFE is sufficiently large). Resistance R1 is calculated as
where K = 1.2 to 2 (so that RR1 is low enough to ensure adequate IB),
and hFE,min is the lowest acceptable current gain for the particular transistor type being used.
LED current source
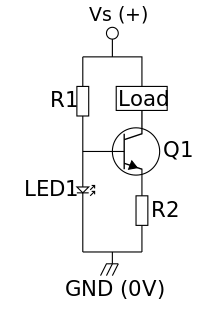
The Zener diode can be replaced by any other diode; e.g., a light-emitting diode LED1 as shown in Figure 5. The LED voltage drop (VD) is now used to derive the constant voltage and also has the additional advantage of tracking (compensating) VBE changes due to temperature. R2 is calculated as
and R1 as
- , where ID is the LED current
Transistor current source with diode compensation

Temperature changes will change the output current delivered by the circuit of Figure 4 because VBE is sensitive to temperature. Temperature dependence can be compensated using the circuit of Figure 6 that includes a standard diode, D, (of the same semiconductor material as the transistor) in series with the Zener diode as shown in the image on the left. The diode drop (VD) tracks the VBE changes due to temperature and thus significantly counteracts temperature dependence of the CCS.
Resistance R2 is now calculated as
Since VD = VBE = 0.65 V,
(In practice, VD is never exactly equal to VBE and hence it only suppresses the change in VBE rather than nulling it out.)
R1 is calculated as
(the compensating diode's forward voltage drop, VD, appears in the equation and is typically 0.65 V for silicon devices.)
Note that this only works well if DZ1 is a reference diode or another stable voltage source. Together with 'normal' Zener diodes especially with lower Zener voltages (<5V) the diode might even worsen overall temperature dependency.
Current mirror with emitter degeneration
Series negative feedback is also used in the two-transistor current mirror with emitter degeneration. Negative feedback is a basic feature in some current mirrors using multiple transistors, such as the Widlar current source and the Wilson current source.
Constant current source with thermal compensation
One limitation with the circuits in Figures 5 and 6 is that the thermal compensation is imperfect. In bipolar transistors, as the junction temperature increases the Vbe drop (voltage drop from base to emitter) decreases. In the two previous circuits, a decrease in Vbe will cause an increase in voltage across the emitter resistor, which in turn will cause an increase in collector current drawn through the load. The end result is that the amount of 'constant' current supplied is at least somewhat dependent on temperature. This effect is mitigated to a large extent, but not completely, by corresponding voltage drops for the diode, D1, in Figure 6, and the LED, LED1, in Figure 5. If the power dissipation in the active device of the CCS is not small and/or insufficient emitter degeneration is used, this can become a non-trivial issue.
Imagine in Figure 5, at power up, that the LED has 1 V across it driving the base of the transistor. At room temperature there is about 0.6 V drop across the Vbe junction and hence 0.4 V across the emitter resistor, giving an approximate collector (load) current of 0.4/Re amps. Now imagine that the power dissipation in the transistor causes it to heat up. This causes the Vbe drop (which was 0.6 V at room temperature) to drop to, say, 0.2 V. Now the voltage across the emitter resistor is 0.8 V, twice what it was before the warmup. This means that the collector (load) current is now twice the design value! This is an extreme example of course, but serves to illustrate the issue.
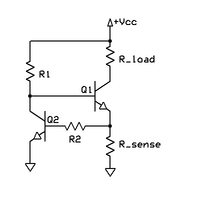
The circuit to the left overcomes the thermal problem (see also, current limiting). To see how the circuit works, assume the voltage has just been applied at V+. Current runs through R1 to the base of Q1, turning it on and causing current to begin to flow through the load into the collector of Q1. This same load current then flows out of Q1's emitter and consequently through Rsense to ground. When this current through Rsense to ground is sufficient to cause a voltage drop that is equal to the Vbe drop of Q2, Q2 begins to turn on. As Q2 turns on it pulls more current through its collector resistor, R1, which diverts some of the injected current in the base of Q1, causing Q1 to conduct less current through the load. This creates a negative feedback loop within the circuit, which keeps the voltage at Q1's emitter almost exactly equal to the Vbe drop of Q2. Since Q2 is dissipating very little power compared to Q1 (since all the load current goes through Q1, not Q2), Q2 will not heat up any significant amount and the reference (current setting) voltage across Rsense will remain steady at ≈0.6 V, or one diode drop above ground, regardless of the thermal changes in the Vbe drop of Q1. The circuit is still sensitive to changes in the ambient temperature in which the device operates as the BE voltage drop in Q2 varies slightly with temperature.
Op-amp current sources
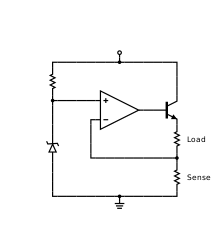
The simple transistor current source from Figure 4 can be improved by inserting the base-emitter junction of the transistor in the feedback loop of an op-amp (Figure 7). Now the op-amp increases its output voltage to compensate for the VBE drop. The circuit is actually a buffered non-inverting amplifier driven by a constant input voltage. It keeps up this constant voltage across the constant sense resistor. As a result, the current flowing through the load is constant as well; it is exactly the Zener voltage divided by the sense resistor. The load can be connected either in the emitter (Figure 7) or in the collector (Figure 4) but in both the cases it is floating as in all the circuits above. The transistor is not needed if the required current doesn't exceed the sourcing ability of the op-amp. The article on current mirror discusses another example of these so-called gain-boosted current mirrors.

Voltage regulator current sources
The general negative feedback arrangement can be implemented by an IC voltage regulator (LM317 voltage regulator on Figure 8). As with the bare emitter follower and the precise op-amp follower above, it keeps up a constant voltage drop (1.25 V) across a constant resistor (1.25 Ω); so, a constant current (1 A) flows through the resistor and the load. The LED is on when the voltage across the load exceeds 1.8 V (the indicator circuit introduces some error). The grounded load is an important advantage of this solution.
Curpistor tubes
Nitrogen-filled glass tubes with two electrodes and a calibrated Becquerel (decays per second) amount of Ra offer a constant number of charge carriers per second for conduction, which determines the maximum current the tube can pass over a voltage range from 25 to 500 V.
Current and voltage source comparison

Most sources of electrical energy (mains electricity, a battery, etc.) are best modeled as voltage sources, however some (notably solar cells) are better modeled using current sources. Sometimes it is easier to view a current source as a voltage source and vice versa (see conversion in Figure 9) using Norton's and Thévenin's theorems.
Voltage sources provide an almost-constant output voltage as long as the current drawn from the source is within the source's capabilities. An ideal voltage source loaded by an open circuit (i.e., an infinite impedance) will provide no current (and hence no power). But when the load resistance approaches zero (a short circuit), the current (and thus power) approach infinity. Such a theoretical device has a zero ohm output impedance in series with the source. Real-world voltage sources instead have a non-zero output impedance, which is preferably very low (often much less than 1 ohm).
Conversely, a current source provides a constant current, as long as the impedance of the load is sufficiently lower than the current source's parallel impedance (which is preferably very high and ideally infinite). In the case of transistor current sources, impedances of a few megohms (at low frequencies) are typical. Because power is current squared times resistance, as a load resistance connected to a current source approaches zero (a short circuit), the current and thus power both approach zero.
Ideal current sources don't exist. Hypothetically connecting one to an ideal open circuit would create the paradox of running a constant, non-zero current (from the current source) through an element with a defined zero current (the open circuit). As the load resistance of an ideal current source approaches infinity (an open circuit), the voltage across the load would approach infinity (because voltage equals current times resistance), and hence the power drawn would also approach infinity. The current of a real current source connected to an open circuit would instead flow through the current source's internal parallel impedance (and be wasted as heat).
Similarly, ideal voltage sources don't exist. Hypothetically connecting one to an ideal short circuit would result a similar paradox of finite non-zero voltage across an element with defined zero voltage (the short circuit).
Just like how voltage sources should not be connected in parallel to another voltage source with different voltages, a current source also should not be connected in series to another current source. Note, some circuits use elements that are similar but not identical to voltage or current sources and may work when connected in these manners that are disallowed for actual current or voltage sources. Also, just like voltage sources may be connected in series to add their voltages, current sources may be connected in parallel to add their currents.
Charging a capacitor
Because the charge on a capacitor is equal to the integral of current with respect to time, an ideal constant current source charges a capacitor linearly with time, regardless of any series resistance. The Wilkinson analog-to-digital converter, for instance, uses this linear behavior to measure an unknown voltage by measuring the amount of time it takes a current source to charge a capacitor to that voltage. A voltage source instead charges a capacitor through a resistor non-linearly with time, because the charging current from the voltage source decreases exponentially with time.
See also
- Constant current
- Current limiting
- Current loop
- Current mirror
- Current sources and sinks
- Fontana bridge, a compensated current source
- Iron-hydrogen resistor
- Saturable reactor
- Voltage-to-current converter
- Welding power supply, a device used for arc welding, many of which are designed as constant current devices.
- Widlar current source
References
- Widlar bilateral current source Archived 2011-06-07 at the Wayback Machine
- "AN-1515 A Comprehensive Study of the Howland Current Pump" (PDF) (PDF). Texas Instruments, Inc. 2013.
- Consider the "Deboo" Single-Supply Integrator
- Horowitz, Paul; Winfield Hill (1989). The Art of Electronics, 2nd Ed. UK: Cambridge University Press. pp. 182. ISBN 0521370957.
- The value for VBE varies logarithmically with current level: for more detail see diode modelling.
- ^ See above note on logarithmic current dependence.
- "Tung-Sol: Curpistor, minute current regulator data sheet" (PDF). Retrieved 26 May 2013.
Further reading
- "Current Sources & Voltage References" Linden T. Harrison; Publ. Elsevier-Newnes 2005; 608-pages; ISBN 0-7506-7752-X
External links
- Current Sources and Current Mirrors
- FET Constant-Current Source/Limiter - Vishay
- JFET Current Source and pSpice Simulation Archived 2016-11-15 at the Wayback Machine
- Using Current Sources / Sinks / Mirrors In Audio Archived 2019-07-17 at the Wayback Machine
- Differential Amplifiers and Current Sources





 , where ID is the LED current
, where ID is the LED current


 with parallel source resistance
with parallel source resistance  can be
can be  with equivalent series resistance
with equivalent series resistance  . The conversion also works in reverse.
. The conversion also works in reverse.