

Air showers are extensive cascades of subatomic particles and ionized nuclei, produced in the atmosphere when a primary cosmic ray enters the atmosphere. Particles of cosmic radiation can be protons, nuclei, electrons, photons, or (rarely) positrons. Upon entering the atmosphere, they interact with molecules and initiate a particle cascade that lasts for several generations, until the energy of the primary particle is fully converted. If the primary particle is a hadron, mostly light mesons like pions and kaons are produced in the first interactions, which then fuel a hadronic shower component that produces shower particles mostly through pion decay. Primary photons and electrons, on the other hand, produce mainly electromagnetic showers. Depending on the energy of the primary particle, the detectable size of the shower can reach several kilometers in diameter.
The air shower phenomenon was unknowingly discovered by Bruno Rossi in 1933 in a laboratory experiment. In 1937 Pierre Auger, unaware of Rossi's earlier report, detected the same phenomenon and investigated it in some detail. He concluded that cosmic-ray particles are of extremely high energies and interact with nuclei high up in the atmosphere, initiating a cascade of secondary interactions that produce extensive showers of subatomic particles.
The most important experiments detecting extensive air showers today are HAWC, LHAASO, the Telescope Array Project and the Pierre Auger Observatory. The latter is the largest observatory for cosmic rays ever built, operating with 4 fluorescence detector buildings and 1600 surface detector stations spanning an area of 3,000 km in the Argentinean desert.
History
In 1933, shortly after the discovery of cosmic radiation by Victor Hess, Bruno Rossi conducted an experiment in the Institute of Physics in Florence, using shielded Geiger counters to confirm the penetrating character of the cosmic radiation. He used different arrangements of Geiger counters, including a setup of three counters, where two were placed next to each other and a third was centered underneath with additional shielding. From the detection of air-shower particles passing through the Geiger counters in coincidence, he assumed that secondary particles are being produced by cosmic rays in the first shielding layer as well as in the rooftop of the laboratory, unknowing that the particles he measured were muons, which are produced in air showers and which would only be discovered three years later. He also noted that the coincidence rate drops significantly for cosmic rays that are detected at a zenith angle below . A similar experiment was conducted in 1936 by Hilgert and Bothe in Heidelberg.
In a publication in 1939, Pierre Auger, together with three colleagues, suggested that secondary particles are created by cosmic rays in the atmosphere, and conducted experiments using shielded scintillators and Wilson chambers on the Jungfraujoch at an altitude of above sea level, and on Pic du Midi at an altitude of above sea level, and at sea level. They found that the rate of coincidences reduces with increasing distance of the detectors, but does not vanish, even at high altitudes. Thus confirming that cosmic rays produce air showers of secondary particles in the atmosphere. They estimated that the primary particles of this phenomenon must have energies of up to .
Based on the idea of quantum theory, theoretical work on air showers was carried between 1935 and 1940 out by many well-known physicists of the time (including Bhabha, Oppenheimer, Landau, Rossi and others), assuming that in the vicinity of nuclear fields high-energy gamma rays will undergo pair-production of electrons and positrons, and electrons and positrons will produce gamma rays by radiation. Work on extensive air showers continued mainly after the war, as many key figures were involved in the Manhattan project. In the 1950s, the lateral and angular structure of electromagnetic particles in air showers were calculated by Japanese scientists Koichi Kamata and Jun Nishimura.
In 1955, the first surface detector array to detect air showers with sufficient precision to detect the arrival direction of the primary cosmic rays was built at the Agassiz station at MIT. The Agassiz array consisted of 16 plastic scintillators arranged in a diameter circular array. The results of the experiment on the arrival directions of cosmic rays, however, where inconclusive.
The Volcano Ranch experiment, which was built in 1959 and operated by John Linsley, was the first surface detector array of sufficient size to detect ultrahigh-energy cosmic rays. In 1962, the first cosmic ray with an energy of was reported. With a footprint of several kilometers, the shower size at the ground was twice as large as any event recorded before, approximately producing particles in the shower. Furthermore, it was confirmed that the lateral distribution of the particles detected at the ground matched Kenneth Greisen's approximation of the structure functions derived by Kamata and Nishimura.
A novel detection technique for extensive air showers was proposed by Greisen in 1965. He suggested to directly observe Cherenkov radiation of the shower particles, and fluorescence light produced by excited nitrogen molecules in the atmosphere. In this way, one would be able to measure the longitudinal development of a shower in the atmosphere. This method was first applied successfully and reported in 1977 at Volcano Ranch, using 67 optical modules. Volcano Ranch finished its operation shortly after due to lack of funding.
Many air-shower experiments followed in the decades after, including KASCADE, AGASA, and HIRES. In 1995, the latter reported the detection of an ultrahigh-energy cosmic ray with an energy beyond the theoretically expected spectral cutoff. The air shower of the cosmic ray was detected by the Fly's Eye fluorescence detector system and was estimated to contain approximately 240 billion particles at its maximum. This corresponds to a primary energy for the cosmic ray of about . To this day, no single particle with a larger energy was recorded. It is therefore publicly referred to as the Oh-My-God particle.
Air shower formation
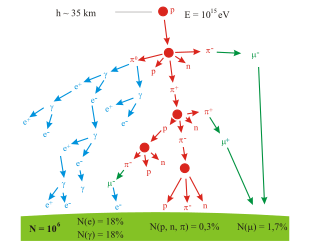
The air shower is formed by interaction of the primary cosmic ray with the atmosphere, and then by subsequent interaction of the secondary particles, and so on. Depending on the type of the primary particle, the shower particles will be created mostly by hadronic or electromagnetic interactions.
Simplified shower model
Shortly after entering the atmosphere, the primary cosmic ray (which is assumed to be a proton or nucleus in the following) is scattered by a nucleus in the atmosphere and creates a shower core - a region of high-energy hadrons that develops along the extended trajectory of the primary cosmic ray, until it is fully absorbed by either the atmosphere or the ground. The interaction and decay of particles in the shower core feeds the main particle components of the shower, which are hadrons, muons, and purely electromagnetic particles. The hadronic part of the shower consists mostly of pions, and some heavier mesons, such as kaons and mesons.
Neutral pions, , decay by the electroweak interaction into pairs of oppositely spinning photons, which fuel the electromagnetic component of the shower. Charged pions, , preferentially decay into muons and (anti)neutrinos via the weak interaction. The same holds true for charged and neutral kaons. In addition, kaons also produce pions. Neutrinos from pion and kaon decay are usually not accounted for as parts of the shower because of their very low cross-section, and are referred to as part of the invisible energy of the shower.

Qualitatively, the particle content of a shower can be described by a simplified model, in which all particles partaking in any interaction of the shower will equally share the available energy. One can assume that in each hadronic interaction, charged pions and neutral pions are produced. The neutral pions will decay into photons, which fuel the electromagnetic part of the shower. The charged pions will then continue to interact hadronically. After interactions, the share of the primary energy deposited in the hadronic component is given by
,
and the electromagnetic part thus approximately carries
.
A pion in the th generation thus carries an energy of . The reaction continues, until the pions reach a critical energy , at which they decay into muons. Thus, a total of
interactions are expected and a total of muons are produced, with . The electromagnetic part of the cascade develops in parallel by bremsstrahlung and pair production. For the sake of simplicity, photons, electrons, and positrons are often treated as equivalent particles in the shower. The electromagnetic cascade continues, until the particles reach a critical energy of , from which on they start losing most of their energy due to scattering with molecules in the atmosphere. Because , the electromagnetic particles dominate the number of particles in the shower by far. A good approximation for the number of (electromagnetic) particles produced in a shower is . Assuming each electromagnetic interaction occurs after the average radiation length , the shower will reach its maximum at a depth of approximately
,
where is assumed to be the depth of the first interaction of the cosmic ray in the atmosphere. This approximation is, however, not accurate for all types of primary particles. Especially showers from heavy nuclei will reach their maximum much earlier.
Longitudinal profile
The number of particles present in an air shower is approximately proportional to the calorimetric energy deposit of the shower. The energy deposit as a function of the surpassed atmospheric matter, as it can for example be seen by fluorescence detector telescopes, is known as the longitudinal profile of the shower. For the longitudinal profile of the shower, only the electromagnetic particles (electrons, positrons, and photons) are relevant, as they dominate the particle content and the contribution to the calorimetric energy deposit.

The shower profile is characterized by a fast rise in the number of particles, before the average energy of the particles falls below around the shower maximum, and a slow decay afterwards. Mathematically the profile can be well described by a slanted Gaussian, the Gaisser-Hillas function or the generalized Greisen function,
Here and using the electromagnetic radiation length in air, . marks the point of the first interaction, and is a dimensionless constant. The shower age parameter is introduced to compare showers with different starting depths and different primary energies to highlight their universal features, as for example at the shower maximum . For a shower with a first interaction at , the shower age is usually defined as
.
The image shows the ideal longitudinal profile of showers using different primary energies, as a function of the surpassed atmospheric depth or, equivalently, the number of radiation lengths .
The longitudinal profiles of showers are particularly interesting in the context of measuring the total calorimetric energy deposit and the depth of the shower maximum, , since the latter is an observable that is sensitive to type of the primary particle. The shower appears brightest in a fluorescence telescope at its maximum.
Lateral profile
For idealized electromagnetic showers, the angular and lateral distribution functions for electromagnetic particles have been derived by Japanese physicists Nishimura and Kamata. For a shower of age , the density of electromagnetic particles as a function of the distance to the shower axis can be approximated by the NKG function
using the number of particles , Molière radius and the common Gamma function. can be given for example by the longitudinal profile function. The lateral distribution of hadronic showers (i.e. initiated by a primary hadron, such as a proton), which contain a significantly increased amount of muons, can be well approximated by a superposition of NKG-like functions, in which different particle components are described using effective values for and .
Detection
The original particle arrives with high energy and hence a velocity near the speed of light, so the products of the collisions tend also to move generally in the same direction as the primary, while to some extent spreading sidewise. In addition, the secondary particles produce a widespread flash of light in forward direction due to the Cherenkov effect, as well as fluorescence light that is emitted isotropically from the excitation of nitrogen molecules. The particle cascade and the light produced in the atmosphere can be detected with surface detector arrays and optical telescopes. Surface detectors typically use Cherenkov detectors or scintillation counters to detect the charged secondary particles at ground level. The telescopes used to measure the fluorescence and Cherenkov light use large mirrors to focus the light on PMT clusters. Finally, air showers emit radio waves due to the deflection of electrons and positrons by the geomagnetic field. As advantage over the optical techniques, radio detection is possible around the clock and not only during dark and clear nights. Thus, several modern experiments, e.g., TAIGA, LOFAR, or the Pierre Auger Observatory use radio antennas in addition to particle detectors and optical techniques.
See also
References
- Auger, P.; et al. (July 1939), "Extensive Cosmic-Ray Showers", Reviews of Modern Physics, 11 (3–4): 288–291, Bibcode:1939RvMP...11..288A, doi:10.1103/RevModPhys.11.288.
- Rossi, Bruno (August 1930). "On the Magnetic Deflection of Cosmic Rays". Physical Review. 36 (3): 606. Bibcode:1930PhRv...36..606R. doi:10.1103/PhysRev.36.606.
- Rossi, Bruno (1933). "Über die Eigenschaften der durchdringenden Korpuskularstrahlung im Meeresniveau". Zeitschrift für Physik (in German). 82 (3–4). Springer Science and Business Media LLC: 151–178. Bibcode:1933ZPhy...82..151R. doi:10.1007/bf01341486. ISSN 1434-6001. S2CID 121427439.
- Hilgert, R.; Bothe, W. (1936). "Zur Struktur der kosmischen Ultrastrahlung". Zeitschrift für Physik (in German). 99 (5–6). Springer Science and Business Media LLC: 353–362. Bibcode:1936ZPhy...99..353H. doi:10.1007/bf01330786. ISSN 1434-6001. S2CID 119935508.
- Auger, Pierre; Ehrenfest, P.; Maze, R.; Daudin, J.; Fréon, Robley A. (1939-07-01). "Extensive Cosmic-Ray Showers". Reviews of Modern Physics. 11 (3–4). American Physical Society (APS): 288–291. Bibcode:1939RvMP...11..288A. doi:10.1103/revmodphys.11.288. ISSN 0034-6861.
- Bhabha; Heitler (1937). "The passage of fast electrons and the theory of cosmic showers". Proceedings of the Royal Society of London. Series A - Mathematical and Physical Sciences. 159 (898). The Royal Society: 432–458. Bibcode:1937RSPSA.159..432B. doi:10.1098/rspa.1937.0082. ISSN 0080-4630.
- Carlson, J. F.; Oppenheimer, J. R. (1937-02-15). "On Multiplicative Showers". Physical Review. 51 (4). American Physical Society (APS): 220–231. Bibcode:1937PhRv...51..220C. doi:10.1103/physrev.51.220. ISSN 0031-899X.
- Landau, L.; Rumer, G. (1938-05-19). "The cascade theory of electronic showers". Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences. 166 (925). The Royal Society: 213–228. Bibcode:1938RSPSA.166..213L. doi:10.1098/rspa.1938.0088. ISSN 0080-4630.
- Rossi, Bruno; Greisen, Kenneth (1941-10-01). "Cosmic-Ray Theory". Reviews of Modern Physics. 13 (4). American Physical Society (APS): 240–309. Bibcode:1941RvMP...13..240R. doi:10.1103/revmodphys.13.240. ISSN 0034-6861.
- Kamata, Koichi; Nishimura, Jun (1958). "The Lateral and the Angular Structure Functions of Electron Showers". Progress of Theoretical Physics Supplement. 6. Oxford University Press (OUP): 93–155. Bibcode:1958PThPS...6...93K. doi:10.1143/ptps.6.93. ISSN 0375-9687.
- CLARK, G.; EARL, J.; KRAUSHAAR, W.; LINSLEY, J.; ROSSI, B.; SCHERB, F. (1957). "An Experiment on Air Showers Produced by High-Energy Cosmic Rays". Nature. 180 (4582). Springer Science and Business Media LLC: 353–356. Bibcode:1957Natur.180..353C. doi:10.1038/180353a0. ISSN 0028-0836. S2CID 4173505.
- Linsley, John (1963-02-15). "Evidence for a Primary Cosmic-Ray Particle with Energy 10^20eV". Physical Review Letters. 10 (4). American Physical Society (APS): 146–148. doi:10.1103/physrevlett.10.146. ISSN 0031-9007.
- Greisen, Kenneth (1960). "Cosmic Ray Showers". Annual Review of Nuclear and Particle Science. 10: 63–108. Bibcode:1960ARNPS..10...63G. doi:10.1146/annurev.ns.10.120160.000431.
- Bergeson, H. E.; Cassiday, G. L.; Chiu, T. -W.; Cooper, D. A.; Elbert, J. W.; Loh, E. C.; Steck, D.; West, W. J.; Linsley, J.; Mason, G. W. (1977-09-26). "Measurement of Light Emission from Remote Cosmic-Ray Air Showers". Physical Review Letters. 39 (13). American Physical Society (APS): 847–849. Bibcode:1977PhRvL..39..847B. doi:10.1103/physrevlett.39.847. ISSN 0031-9007.
- Oh-My-God particle
- Bird, D. J.; Corbato, S. C.; Dai, H. Y.; Elbert, J. W.; Green, K. D.; Huang, M. A.; Kieda, D. B.; Ko, S.; Larsen, C. G.; Loh, E. C.; Luo, M. Z.; Salamon, M. H.; Smith, J. D.; Sokolsky, P.; Sommers, P.; Tang, J. K. K.; Thomas, S. B. (1995). "Detection of a cosmic ray with measured energy well beyond the expected spectral cutoff due to cosmic microwave radiation". The Astrophysical Journal. 441. American Astronomical Society: 144. arXiv:astro-ph/9410067. Bibcode:1995ApJ...441..144B. doi:10.1086/175344. ISSN 0004-637X.
- Gaisser, T. K., Engel, R., & Resconi, E. (2016). Cosmic Rays and Particle Physics: 2nd Edition. Cambridge University Press.
- ^ Rao, M. (1998). Extensive Air Showers. World Scientific. p. 10. ISBN 9789810228880.
- Matthews, J. (2005). "A Heitler model of extensive air showers". Astroparticle Physics. 22 (5–6). Elsevier BV: 387–397. Bibcode:2005APh....22..387M. doi:10.1016/j.astropartphys.2004.09.003. ISSN 0927-6505.
- Kamata, Koichi; Nishimura, Jun (1958). "The Lateral and the Angular Structure Functions of Electron Showers". Progress of Theoretical Physics Supplement. 6. Oxford University Press (OUP): 93–155. Bibcode:1958PThPS...6...93K. doi:10.1143/ptps.6.93. ISSN 0375-9687.
- Greisen, Kennet (1960). "Cosmic Ray Showers". Annual Review of Nuclear and Particle Science. 10: 63–108. Bibcode:1960ARNPS..10...63G. doi:10.1146/annurev.ns.10.120160.000431.
External links
- Extensive Air Showers.
- Buckland Park Air Shower Detector
- Haverah Park Detection System
- HiRes Detector System
- Pierre Auger Observatory
- HiSPARC (High School Project on Astrophysics Research with Cosmics)
- AIRES (AIRshower Extended Simulations) : Large and well documented Fortran package for simulating cosmic ray showers by Sergio Sciutto at the Department of Physics of the Universidad Nacional de La Plata, Argentina
- CORSIKA, CORSIKA: Another code for simulating cosmic ray air showers by Dieter Heck of the Forschungszentrum Karlsruhe, Germany
- COSMUS : Interactive animated 3d models of several different cosmic ray air showers, and instructions on how to make your own using AIRES simulations. From the COSMUS group at the University of Chicago.
- Milagro Animations : Movies and instructions for how to make them, showing how air showers interact with the Milagro detector. By Miguel Morales.
- CASSIM Animations : Animations of different cosmic ray air showers by Hajo Dreschler of New York University.
- SPASE2 Experiment : South-Pole Air Shower Experiment (SPASE).
- GAMMA Experiment : High mountain Air Shower Experiment.
 .
A similar experiment was conducted in 1936 by Hilgert and Bothe in
.
A similar experiment was conducted in 1936 by Hilgert and Bothe in  above sea level, and on
above sea level, and on  above sea level, and at sea level. They found that the rate of coincidences reduces with increasing distance of the detectors, but does not vanish, even at high altitudes. Thus confirming that cosmic rays produce air showers of secondary particles in the atmosphere.
They estimated that the primary particles of this phenomenon must have energies of up to
above sea level, and at sea level. They found that the rate of coincidences reduces with increasing distance of the detectors, but does not vanish, even at high altitudes. Thus confirming that cosmic rays produce air showers of secondary particles in the atmosphere.
They estimated that the primary particles of this phenomenon must have energies of up to  .
.
 diameter circular array. The results of the experiment on the arrival directions of cosmic rays, however, where inconclusive.
diameter circular array. The results of the experiment on the arrival directions of cosmic rays, however, where inconclusive.
 was reported. With a footprint of several kilometers, the shower size at the ground was twice as large as any event recorded before, approximately producing
was reported. With a footprint of several kilometers, the shower size at the ground was twice as large as any event recorded before, approximately producing  particles in the shower. Furthermore, it was confirmed that the lateral distribution of the particles detected at the ground matched
particles in the shower. Furthermore, it was confirmed that the lateral distribution of the particles detected at the ground matched  . To this day, no single particle with a larger energy was recorded. It is therefore publicly referred to as the
. To this day, no single particle with a larger energy was recorded. It is therefore publicly referred to as the  mesons.
mesons.
 , decay by the
, decay by the  , preferentially decay into
, preferentially decay into  charged pions and
charged pions and  neutral pions are produced. The neutral pions will decay into photons, which fuel the electromagnetic part of the shower. The charged pions will then continue to interact hadronically. After
neutral pions are produced. The neutral pions will decay into photons, which fuel the electromagnetic part of the shower. The charged pions will then continue to interact hadronically. After  interactions, the share of the primary energy
interactions, the share of the primary energy  deposited in the hadronic component is given by
deposited in the hadronic component is given by
 ,
,
 .
.
 . The reaction continues, until the pions reach a critical energy
. The reaction continues, until the pions reach a critical energy  , at which they decay into muons. Thus, a total of
, at which they decay into muons. Thus, a total of

 muons are produced, with
muons are produced, with  . The electromagnetic part of the cascade develops in parallel by
. The electromagnetic part of the cascade develops in parallel by  , from which on they start losing most of their energy due to
, from which on they start losing most of their energy due to  , the electromagnetic particles dominate the number of particles in the shower by far. A good approximation for the number of (electromagnetic) particles produced in a shower is
, the electromagnetic particles dominate the number of particles in the shower by far. A good approximation for the number of (electromagnetic) particles produced in a shower is  . Assuming each electromagnetic interaction occurs after the average radiation length
. Assuming each electromagnetic interaction occurs after the average radiation length  , the shower will reach its maximum at a depth of approximately
, the shower will reach its maximum at a depth of approximately
 ,
,
 is assumed to be the depth of the first interaction of the cosmic ray in the atmosphere. This approximation is, however, not accurate for all types of primary particles. Especially showers from heavy nuclei will reach their maximum much earlier.
is assumed to be the depth of the first interaction of the cosmic ray in the atmosphere. This approximation is, however, not accurate for all types of primary particles. Especially showers from heavy nuclei will reach their maximum much earlier.
 around the shower maximum, and a slow decay afterwards. Mathematically the profile can be well described by a slanted Gaussian, the
around the shower maximum, and a slow decay afterwards. Mathematically the profile can be well described by a slanted Gaussian, the 
 and
and  using the electromagnetic radiation length in air,
using the electromagnetic radiation length in air,  .
.  marks the point of the first interaction, and
marks the point of the first interaction, and  is a dimensionless constant.
The shower age parameter
is a dimensionless constant.
The shower age parameter  is introduced to compare showers with different starting depths and different primary energies to highlight their universal features, as for example at the shower maximum
is introduced to compare showers with different starting depths and different primary energies to highlight their universal features, as for example at the shower maximum  . For a shower with a first interaction at
. For a shower with a first interaction at  , the shower age
, the shower age  .
.
 or, equivalently, the number of radiation lengths
or, equivalently, the number of radiation lengths  .
.
 , since the latter is an observable that is sensitive to type of the primary particle.
The shower appears brightest in a fluorescence telescope at its maximum.
, since the latter is an observable that is sensitive to type of the primary particle.
The shower appears brightest in a fluorescence telescope at its maximum.
 to the shower axis can be approximated by the NKG function
to the shower axis can be approximated by the NKG function

 , Molière radius
, Molière radius  and the common
and the common