
- tangent basis
- e1, e2, e3 to the coordinate curves (left),
- dual basis, covector basis, or reciprocal basis
- e, e, e to coordinate surfaces (right),
In physics, especially in multilinear algebra and tensor analysis, covariance and contravariance describe how the quantitative description of certain geometric or physical entities changes with a change of basis. Briefly, a contravariant vector is a list of numbers that transforms oppositely to a change of basis, and a covariant vector is a list of numbers that transforms in the same way. Contravariant vectors are often just called vectors and covariant vectors are called covectors or dual vectors. The terms covariant and contravariant were introduced by James Joseph Sylvester in 1851.
Curvilinear coordinate systems, such as cylindrical or spherical coordinates, are often used in physical and geometric problems. Associated with any coordinate system is a natural choice of coordinate basis for vectors based at each point of the space, and covariance and contravariance are particularly important for understanding how the coordinate description of a vector changes by passing from one coordinate system to another. Tensors are objects in multilinear algebra that can have aspects of both covariance and contravariance.
Introduction
In physics, a vector typically arises as the outcome of a measurement or series of measurements, and is represented as a list (or tuple) of numbers such as
The numbers in the list depend on the choice of coordinate system. For instance, if the vector represents position with respect to an observer (position vector), then the coordinate system may be obtained from a system of rigid rods, or reference axes, along which the components v1, v2, and v3 are measured. For a vector to represent a geometric object, it must be possible to describe how it looks in any other coordinate system. That is to say, the components of the vectors will transform in a certain way in passing from one coordinate system to another.
A simple illustrative case is that of a Euclidean vector. For a vector, once a set of basis vectors has been defined, then the components of that vector will always vary opposite to that of the basis vectors. That vector is therefore defined as a contravariant tensor. Take a standard position vector for example. By changing the scale of the reference axes from meters to centimeters (that is, dividing the scale of the reference axes by 100, so that the basis vectors now are meters long), the components of the measured position vector are multiplied by 100. A vector's components change scale inversely to changes in scale to the reference axes, and consequently a vector is called a contravariant tensor.
A vector, which is an example of a contravariant tensor, has components that transform inversely to the transformation of the reference axes, (with example transformations including rotation and dilation). The vector itself does not change under these operations; instead, the components of the vector change in a way that cancels the change in the spatial axes. In other words, if the reference axes were rotated in one direction, the component representation of the vector would rotate in exactly the opposite way. Similarly, if the reference axes were stretched in one direction, the components of the vector, would reduce in an exactly compensating way. Mathematically, if the coordinate system undergoes a transformation described by an invertible matrix M, so that the basis vectors transform according to , then the components of a vector v in the original basis ( ) must be similarly transformed via . The components of a vector are often represented arranged in a column.
By contrast, a covector has components that transform like the reference axes. It lives in the dual vector space, and represents a linear map from vectors to scalars. The dot product operator involving vectors is a good example of a covector. To illustrate, assume we have a covector defined as , where is a vector. The components of this covector in some arbitrary basis are , with being the basis vectors in the corresponding vector space. (This can be derived by noting that we want to get the correct answer for the dot product operation when multiplying by an arbitrary vector , with components ). The covariance of these covector components is then seen by noting that if a transformation described by an invertible matrix M were to be applied to the basis vectors in the corresponding vector space, , then the components of the covector will transform with the same matrix , namely, . The components of a covector are often represented arranged in a row.
A third concept related to covariance and contravariance is invariance. A scalar (also called type-0 or rank-0 tensor) is an object that does not vary with the change in basis. An example of a physical observable that is a scalar is the mass of a particle. The single, scalar value of mass is independent to changes in basis vectors and consequently is called invariant. The magnitude of a vector (such as distance) is another example of an invariant, because it remains fixed even if geometrical vector components vary. (For example, for a position vector of length meters, if all Cartesian basis vectors are changed from meters in length to meters in length, the length of the position vector remains unchanged at meters, although the vector components will all increase by a factor of ). The scalar product of a vector and a covector is invariant, because one has components that vary with the base change, and the other has components that vary oppositely, and the two effects cancel out. One thus says that covectors are dual to vectors.
Thus, to summarize:
- A vector or tangent vector, has components that contra-vary with a change of basis to compensate. That is, the matrix that transforms the vector components must be the inverse of the matrix that transforms the basis vectors. The components of vectors (as opposed to those of covectors) are said to be contravariant. In Einstein notation (implicit summation over repeated index), contravariant components are denoted with upper indices as in
- A covector or cotangent vector has components that co-vary with a change of basis in the corresponding (initial) vector space. That is, the components must be transformed by the same matrix as the change of basis matrix in the corresponding (initial) vector space. The components of covectors (as opposed to those of vectors) are said to be covariant. In Einstein notation, covariant components are denoted with lower indices as in
- The scalar product of a vector and covector is the scalar , which is invariant. It is the duality pairing of vectors and covectors.
Definition

The general formulation of covariance and contravariance refers to how the components of a coordinate vector transform under a change of basis (passive transformation). Thus let V be a vector space of dimension n over a field of scalars S, and let each of f = (X1, ..., Xn) and f′ = (Y1, ..., Yn) be a basis of V. Also, let the change of basis from f to f′ be given by
| 1 |
for some invertible n×n matrix A with entries . Here, each vector Yj of the f′ basis is a linear combination of the vectors Xi of the f basis, so that
Contravariant transformation
Main article: Contravariant transformationA vector in V is expressed uniquely as a linear combination of the elements of the f basis as
| 2 |
where v are elements of the field S known as the components of v in the f basis. Denote the column vector of components of v by v:
so that (2) can be rewritten as a matrix product
The vector v may also be expressed in terms of the f′ basis, so that
However, since the vector v itself is invariant under the choice of basis,
The invariance of v combined with the relationship (1) between f and f′ implies that
giving the transformation rule
In terms of components,
where the coefficients are the entries of the inverse matrix of A.
Because the components of the vector v transform with the inverse of the matrix A, these components are said to transform contravariantly under a change of basis.
The way A relates the two pairs is depicted in the following informal diagram using an arrow. The reversal of the arrow indicates a contravariant change:
Covariant transformation
Main article: Covariant transformationA linear functional α on V is expressed uniquely in terms of its components (elements in S) in the f basis as
These components are the action of α on the basis vectors Xi of the f basis.
Under the change of basis from f to f′ (via 1), the components transform so that
| 3 |
Denote the row vector of components of α by α:
so that (3) can be rewritten as the matrix product
Because the components of the linear functional α transform with the matrix A, these components are said to transform covariantly under a change of basis.
The way A relates the two pairs is depicted in the following informal diagram using an arrow. A covariant relationship is indicated since the arrows travel in the same direction:
Had a column vector representation been used instead, the transformation law would be the transpose
Coordinates
The choice of basis f on the vector space V defines uniquely a set of coordinate functions on V, by means of
The coordinates on V are therefore contravariant in the sense that
Conversely, a system of n quantities v that transform like the coordinates x on V defines a contravariant vector (or simply vector). A system of n quantities that transform oppositely to the coordinates is then a covariant vector (or covector).
This formulation of contravariance and covariance is often more natural in applications in which there is a coordinate space (a manifold) on which vectors live as tangent vectors or cotangent vectors. Given a local coordinate system x on the manifold, the reference axes for the coordinate system are the vector fields
This gives rise to the frame f = (X1, ..., Xn) at every point of the coordinate patch.
If y is a different coordinate system and
then the frame f' is related to the frame f by the inverse of the Jacobian matrix of the coordinate transition:
Or, in indices,
A tangent vector is by definition a vector that is a linear combination of the coordinate partials . Thus a tangent vector is defined by
Such a vector is contravariant with respect to change of frame. Under changes in the coordinate system, one has
Therefore, the components of a tangent vector transform via
Accordingly, a system of n quantities v depending on the coordinates that transform in this way on passing from one coordinate system to another is called a contravariant vector.
Covariant and contravariant components of a vector with a metric
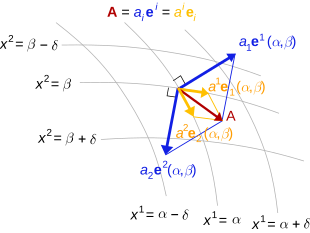
In a finite-dimensional vector space V over a field K with a symmetric bilinear form g : V × V → K (which may be referred to as the metric tensor), there is little distinction between covariant and contravariant vectors, because the bilinear form allows covectors to be identified with vectors. That is, a vector v uniquely determines a covector α via
for all vectors w. Conversely, each covector α determines a unique vector v by this equation. Because of this identification of vectors with covectors, one may speak of the covariant components or contravariant components of a vector, that is, they are just representations of the same vector using the reciprocal basis.
Given a basis f = (X1, ..., Xn) of V, there is a unique reciprocal basis f = (Y, ..., Y) of V determined by requiring that
the Kronecker delta. In terms of these bases, any vector v can be written in two ways:
The components v are the contravariant components of the vector v in the basis f, and the components vi are the covariant components of v in the basis f. The terminology is justified because under a change of basis,
Euclidean plane
In the Euclidean plane, the dot product allows for vectors to be identified with covectors. If is a basis, then the dual basis satisfies
Thus, e and e2 are perpendicular to each other, as are e and e1, and the lengths of e and e normalized against e1 and e2, respectively.
Example
For example, suppose that we are given a basis e1, e2 consisting of a pair of vectors making a 45° angle with one another, such that e1 has length 2 and e2 has length 1. Then the dual basis vectors are given as follows:
- e is the result of rotating e1 through an angle of 90° (where the sense is measured by assuming the pair e1, e2 to be positively oriented), and then rescaling so that e ⋅ e2 = 1 holds.
- e is the result of rotating e2 through an angle of 90°, and then rescaling so that e ⋅ e1 = 1 holds.
Applying these rules, we find
and
Thus the change of basis matrix in going from the original basis to the reciprocal basis is
since
For instance, the vector
is a vector with contravariant components
The covariant components are obtained by equating the two expressions for the vector v:
so
Three-dimensional Euclidean space
In the three-dimensional Euclidean space, one can also determine explicitly the dual basis to a given set of basis vectors e1, e2, e3 of E3 that are not necessarily assumed to be orthogonal nor of unit norm. The dual basis vectors are:
Even when the ei and e are not orthonormal, they are still mutually reciprocal:
Then the contravariant components of any vector v can be obtained by the dot product of v with the dual basis vectors:
Likewise, the covariant components of v can be obtained from the dot product of v with basis vectors, viz.
Then v can be expressed in two (reciprocal) ways, viz.
or
Combining the above relations, we have
and we can convert between the basis and dual basis with
and
If the basis vectors are orthonormal, then they are the same as the dual basis vectors.
General Euclidean spaces
More generally, in an n-dimensional Euclidean space V, if a basis is
the reciprocal basis is given by (double indices are summed over),
where the coefficients g are the entries of the inverse matrix of
Indeed, we then have
The covariant and contravariant components of any vector
are related as above by
and
Use in tensor analysis
The distinction between covariance and contravariance is particularly important for computations with tensors, which often have mixed variance. This means that they have both covariant and contravariant components, or both vector and covector components. The valence of a tensor is the number of covariant and contravariant terms, and in Einstein notation, covariant components have lower indices, while contravariant components have upper indices. The duality between covariance and contravariance intervenes whenever a vector or tensor quantity is represented by its components, although modern differential geometry uses more sophisticated index-free methods to represent tensors.
In tensor analysis, a covariant vector varies more or less reciprocally to a corresponding contravariant vector. Expressions for lengths, areas and volumes of objects in the vector space can then be given in terms of tensors with covariant and contravariant indices. Under simple expansions and contractions of the coordinates, the reciprocity is exact; under affine transformations the components of a vector intermingle on going between covariant and contravariant expression.
On a manifold, a tensor field will typically have multiple, upper and lower indices, where Einstein notation is widely used. When the manifold is equipped with a metric, covariant and contravariant indices become very closely related to one another. Contravariant indices can be turned into covariant indices by contracting with the metric tensor. The reverse is possible by contracting with the (matrix) inverse of the metric tensor. Note that in general, no such relation exists in spaces not endowed with a metric tensor. Furthermore, from a more abstract standpoint, a tensor is simply "there" and its components of either kind are only calculational artifacts whose values depend on the chosen coordinates.
The explanation in geometric terms is that a general tensor will have contravariant indices as well as covariant indices, because it has parts that live in the tangent bundle as well as the cotangent bundle.
A contravariant vector is one which transforms like , where are the coordinates of a particle at its proper time . A covariant vector is one which transforms like , where is a scalar field.
Algebra and geometry
In category theory, there are covariant functors and contravariant functors. The assignment of the dual space to a vector space is a standard example of a contravariant functor. Contravariant (resp. covariant) vectors are contravariant (resp. covariant) functors from a -torsor to the fundamental representation of . Similarly, tensors of higher degree are functors with values in other representations of . However, some constructions of multilinear algebra are of "mixed" variance, which prevents them from being functors.
In differential geometry, the components of a vector relative to a basis of the tangent bundle are covariant if they change with the same linear transformation as a change of basis. They are contravariant if they change by the inverse transformation. This is sometimes a source of confusion for two distinct but related reasons. The first is that vectors whose components are covariant (called covectors or 1-forms) actually pull back under smooth functions, meaning that the operation assigning the space of covectors to a smooth manifold is actually a contravariant functor. Likewise, vectors whose components are contravariant push forward under smooth mappings, so the operation assigning the space of (contravariant) vectors to a smooth manifold is a covariant functor. Secondly, in the classical approach to differential geometry, it is not bases of the tangent bundle that are the most primitive object, but rather changes in the coordinate system. Vectors with contravariant components transform in the same way as changes in the coordinates (because these actually change oppositely to the induced change of basis). Likewise, vectors with covariant components transform in the opposite way as changes in the coordinates.
See also
- Active and passive transformation
- Mixed tensor
- Two-point tensor, a generalization allowing indices to reference multiple vector bases
Notes
- A basis f may here profitably be viewed as a linear isomorphism from R to V. Regarding f as a row vector whose entries are the elements of the basis, the associated linear isomorphism is then
Citations
- Misner, C.; Thorne, K.S.; Wheeler, J.A. (1973). Gravitation. W.H. Freeman. ISBN 0-7167-0344-0.
- Frankel, Theodore (2012). The geometry of physics : an introduction. Cambridge: Cambridge University Press. p. 42. ISBN 978-1-107-60260-1. OCLC 739094283.
- Sylvester, J.J. (1851). "On the general theory of associated algebraical forms". Cambridge and Dublin Mathematical Journal. Vol. 6. pp. 289–293.
- Sylvester, J.J. University Press (16 February 2012). The collected mathematical papers of James Joseph Sylvester. Vol. 3, 1870–1883. Cambridge University Press. ISBN 978-1107661431. OCLC 758983870.
- Bowen, Ray; Wang, C.-C. (2008) . "§3.14 Reciprocal Basis and Change of Basis". Introduction to Vectors and Tensors. Dover. pp. 78, 79, 81. ISBN 9780486469140.
References
- Kusse, Bruce R.; Westwig, Erik A. (2010), Mathematical Physics: Applied Mathematics for Scientists and Engineers (2nd ed.), Wiley, ISBN 978-3-527-61814-9.
- Arfken, George B.; Weber, Hans J. (2005), Mathematical Methods for Physicists (6th ed.), Harcourt, ISBN 0-12-059876-0.
- Dodson, C. T. J.; Poston, T. (1991), Tensor geometry, Graduate Texts in Mathematics, vol. 130 (2nd ed.), Springer, ISBN 978-3-540-52018-4, MR 1223091.
- Greub, Werner Hildbert (1967), Multilinear algebra, Die Grundlehren der Mathematischen Wissenschaften, Band 136, Springer, ISBN 9780387038278, MR 0224623.
- Sternberg, Shlomo (1983), Lectures on differential geometry, Chelsea, ISBN 978-0-8284-0316-0.
- Sylvester, J.J. (1853), "On a Theory of the Syzygetic Relations of Two Rational Integral Functions, Comprising an Application to the Theory of Sturm's Functions, and That of the Greatest Algebraical Common Measure", Philosophical Transactions of the Royal Society of London, 143: 407–548, doi:10.1098/rstl.1853.0018, JSTOR 108572.
- Weinreich, Gabriel (1998), Geometrical Vectors, Chicago Lectures in Physics, The University of Chicago Press, p. 126, ISBN 9780226890487
External links
- "Covariant tensor", Encyclopedia of Mathematics, EMS Press, 2001
- "Contravariant tensor", Encyclopedia of Mathematics, EMS Press, 2001
- Weisstein, Eric W. "Covariant Tensor". MathWorld.
- Weisstein, Eric W. "Contravariant Tensor". MathWorld.
- Invariance, Contravariance, and Covariance
- Dullemond, Kees; Peeters, Kasper (2010). "Introduction to tensor calculus" (PDF).
| Tensors | |||||
|---|---|---|---|---|---|
| Glossary of tensor theory | |||||
| Scope |
| ||||
| Notation | |||||
| Tensor definitions | |||||
| Operations | |||||
| Related abstractions | |||||
| Notable tensors |
| ||||
| Mathematicians | |||||

 meters long), the components of the measured
meters long), the components of the measured 
 , then the components of a vector v in the original basis (
, then the components of a vector v in the original basis (  ) must be similarly transformed via
) must be similarly transformed via  . The components of a vector are often represented arranged in a column.
. The components of a vector are often represented arranged in a column.
 , where
, where  is a vector. The components of this covector in some arbitrary basis are
is a vector. The components of this covector in some arbitrary basis are  , with
, with  being the basis vectors in the corresponding vector space. (This can be derived by noting that we want to get the correct answer for the dot product operation when multiplying by an arbitrary vector
being the basis vectors in the corresponding vector space. (This can be derived by noting that we want to get the correct answer for the dot product operation when multiplying by an arbitrary vector  , with components
, with components  ). The covariance of these covector components is then seen by noting that if a transformation described by an
). The covariance of these covector components is then seen by noting that if a transformation described by an  , namely,
, namely,  . The components of a covector are often represented arranged in a row.
. The components of a covector are often represented arranged in a row.
 meters, if all
meters, if all  meters in length to
meters in length to  ). The scalar product of a vector and a covector is invariant, because one has components that vary with the base change, and the other has components that vary oppositely, and the two effects cancel out. One thus says that covectors are dual to vectors.
). The scalar product of a vector and a covector is invariant, because one has components that vary with the base change, and the other has components that vary oppositely, and the two effects cancel out. One thus says that covectors are dual to vectors.


 , which is invariant. It is the duality pairing of vectors and covectors.
, which is invariant. It is the duality pairing of vectors and covectors.
 .
Here, each vector Yj of the f′ basis is a linear combination of the vectors Xi of the f basis, so that
.
Here, each vector Yj of the f′ basis is a linear combination of the vectors Xi of the f basis, so that

 in V is expressed uniquely as a
in V is expressed uniquely as a  of the f basis as
of the f basis as








 are the entries of the
are the entries of the 












 . Thus a tangent vector is defined by
. Thus a tangent vector is defined by







 is a basis, then the dual basis
is a basis, then the dual basis  satisfies
satisfies

























 , where
, where  are the coordinates of a particle at its
are the coordinates of a particle at its  . A covariant vector is one which transforms like
. A covariant vector is one which transforms like  , where
, where  is a scalar field.
is a scalar field.
 -
-